Abstract
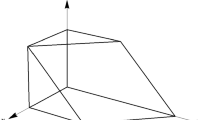
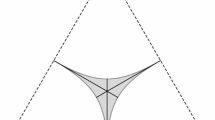
In this work, we describe a set of coordinates on the PU(2,1)-representation variety of the fundamental group of an oriented punctured surface Σ with negative Euler characteristic. The main technical tool we use is a set of geometric invariants of a triple of flags in the complex hyperbolic plane \({\bf H^2_{\mathbb {C}}}\) . We establish a bijection between a set of decorations of an ideal triangulation of Σ and a subset of the PU(2,1)-representation variety of π 1(Σ).
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Falbel E., Koseleff P.V.: Rigidity and flexibility of triangle groups in complex hyperbolic geometry. Topology 41(4), 767–786 (2002)
Falbel E., Parker J.: The moduli space of the modular group in complex hyperbolic geometry. Inv. Math. 152(1), 57–88 (2003)
Falbel E., Platis I.: The PU(2,1)-configuration space of four points in S 3 and the Cross-Ratio Variety. Math. Ann. 340(4), 935–962 (2008)
Fock V., Goncharov A.B.: Moduli spaces of convex projective structures on surfaces. Adv. Math. 208(1), 249–273 (2007)
Fock V., Goncharov A.B.: Moduli spaces of local systems and higher Teichmüller theory. Publ. Math. Inst. Hautes Etudes Sci. 103, 1–211 (2006)
Goldman, W.: Representations of fundamental groups of surfaces. In: Geometry and Topology (College Park, Md., 1983/84), pp. 95–117. Springer (1985)
Goldman W.: Complex Hyperbolic Geometry. Oxford University Press, Oxford (1999)
Goldman W., Kapovich M., Leeb B.: Complex hyperbolic manifolds homotopy equivalent to a Riemann surface. Comm. Anal. Math. 9, 61–95 (2001)
Goldman W., Parker J.: Complex hyperbolic ideal triangle groups. J. für dir reine und angewandte Math. 425, 71–86 (1992)
Koranyi A., Reimann H.M.: The complex cross-ratio on the Heisenberg group. L’Enseign. Math. 33, 291–300 (1987)
Parker J., Platis I.: Complex hyperbolic Fenchel-Nielsen coordinates. Topology 47(2), 101–135 (2008)
Parker J., Platis I.: Open sets of maximal dimension in complex hyperbolic quasi-fuchsian space. J. Diff. Geom. 73, 319–350 (2006)
Pratoussevitch A.: Traces in complex hyperbolic triangle groups. Geometriae Dedicata 111, 159–185 (2005)
Schwartz R. E.: Complex hyperbolic triangle groups. Proc. Int. Math. Cong. 1, 339–350 (2002)
Toledo D.: Representations of surface groups in complex hyperbolic space. J. Differ. Geom. 29, 125–133 (1989)
Will, P.: Groupes libres, groupes triangulaires et tore épointé dans PU(2,1). Thèse de l’université Paris VI.
Will P.: Traces, Cross-ratios and 2-generator Subgroups of PU(2,1). Can. J. Math. 61, 1407–1436 (2009)
Will P.: The punctured torus and Lagrangian triangle groups in PU(2,1). J. reine angew. Math. 602, 95–121 (2007)
Will, P.: Bending Fuchsian representations of fundamental groups of cupsed surfaces in PU(2,1). To appear in J. differ. Geom.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Marché, J., Will, P. Configurations of flags and representations of surface groups in complex hyperbolic geometry. Geom Dedicata 156, 49–70 (2012). https://doi.org/10.1007/s10711-011-9589-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10711-011-9589-9