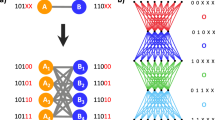
Abstract
There are various representations for encoding graph structures, such as artificial neural networks (ANNs) and circuits, each with its own strengths and weaknesses. Here we analyze edge encodings and show that they produce graphs with a node creation order connectivity bias (NCOCB). Additionally, depending on how input/output (I/O) nodes are handled, it can be difficult to generate ANNs with the correct number of I/O nodes. We compare two edge encoding languages, one which explicitly creates I/O nodes and one which connects to pre-existing I/O nodes with parameterized connection operators. Results from experiments show that these parameterized operators greatly improve the probability of creating and maintaining networks with the correct number of I/O nodes, remove the connectivity bias with I/O nodes and produce better ANNs. These results suggest that evolution with a representation which does not have the NCOCB will produce better performing ANNs. Finally we close with a discussion on which directions hold the most promise for future work in developing better representations for graph structures.











Similar content being viewed by others
Notes
Previously this language was called SEEL, for Standard Edge Encoding Language [14].
PlayStation is a registered trademark of Sony Computer Entertainment Inc.
Animations of goal-scorers controlled with ANNs evolved using both CEEL and PEEL are available online at: http://ic.arc.nasa.gov/people/hornby/evo_control/evo_control.html.
References
P. J. Angeline, “Morphogenic evolutionary computations: Introduction, issues and examples,” in Proc. of the Fourth Annual Conf. on Evolutionary Programming, J. McDonnell, B. Reynolds, and D. Fogel (eds.), MIT Press, 1995, pp. 387–401.
P. J. Angeline, G. M. Saunders, and J. B. Pollack, “An evolutionary algorithm that constructs recurrent neural networks,” IEEE Transactions on Neural Networks, vol. 5, pp. 54–65, 1994.
R. D. Beer and J. G. Gallagher, “Evolving dynamical neural networks for adaptive behavior,” Adaptive Behavior, vol. 1, pp. 91–122, 1992.
P. Bentley and S. Kumar, “Three ways to grow designs: A comparison of embryogenies of an evolutionary design problem,” in Genetic and Evolutionary Computation Conference, W. Banzhaf, J. Daida, A. E. Eiben, M. H. Garzon, V. Honavar, M. Jakiela, and R. E. Smith (eds.), Morgan Kaufmann, 1999, pp. 35–43.
E. J. W. Boers, H. Kuiper, B. L. M. Happel, and I. G. Sprinkhuizen-Kuyper, “Designing modular artificial neural networks,” in Proc. of Computing Science in The Netherlands, H. A. Wijshoff (ed.), SION, Stichting Mathematisch Centrum, 1993, pp. 87–96.
K. E. Drexler, “Biological and nanomechanical systems,” in Artificial Life, C. G. Langton (ed.), Addison Wesley, 1989, pp. 501–519.
F. D. Francone, M. Conrads, W. Banzhaf, and P. Nordin, “Homologous crossover in genetic programming,” in Proceedings of the Genetic and Evolutionary Computation Conference, Orlando, Florida, USA, W. Banzhaf, J. Daida, A. E. Eiben, M. H. Garzon, V. Honavar, M. Jakiela, and R. E. Smith (eds.), Morgan Kaufmann, 1999, vol. 2, pp. 1021–1026.
K. Fredriksson, “Genetic algorithms and generative encoding of neural networks for some benchmark classification problems,” in Proc. of the Third Nordic Workshop on Genetic Algorithms and their Applications, Finnish Artificial Intelligence Society, 1997, pp. 123–134.
C. M. Friedrich and C. Moraga, “An evolutionary method to find good building-blocks for architectures of artificial neural networks,” in Proc. of the Sixth Intl. Conf. on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Granada, Spain, 1996, pp. 951–956.
F. Gruau, Neural Network Synthesis Using Cellular Encoding and the Genetic Algorithm. PhD thesis, Ecole Normale Supérieure de Lyon, 1994.
F. Gruau, “Automatic definition of modular neural networks,” Adaptive Behavior, vol. 3, pp. 151–183, 1995.
P. C. Haddow, G. Tufte, and P. van Remortel, “Shrinking the genotype: L-systems for EHW?” in Proc. of the Fourth International Conference on Evolvable Systems: From Biology to Hardware, Y. Liu, K. Tanaka, M. Iwata, T. Higuchi, and M. Yasunaga (eds.), Lecture Notes in Computer Science; Springer-Verlag, vol. 2210, 2001, pp. 128–139.
G. S. Hornby, Generative Representations for Evolutionary Design Automation. PhD thesis, Michtom School of Computer Science, Brandeis University, Waltham, MA, 2003.
G. S. Hornby, “Shortcomings with tree-structured edge encodings for neural networks,” in Proc. of the Genetic and Evolutionary Computation Conference, Vol. II, K. Deb et al. (eds.), LNCS 3103, Springer-Verlag, New York, 2004, pp. 495–506.
G. S. Hornby, “Measuring, enabling and comparing modularity, regularity and hierarchy in evolutionary design,” in Proc. of the Genetic and Evolutionary Computation Conference, GECCO-2005, New York, H.-G. Beyer et al. (eds.), ACM Press, 2005, pp. 1729–1736.
G. S. Hornby and B. Mirtich, “Diffuse versus true coevolution in a physics-based world,” in Proc. of the Genetic and Evolutionary Computation Conference, W. Banzhaf et al. (eds.), Morgan Kaufmann, 1999, pp. 1305–1312.
G. S. Hornby and J. B. Pollack, “Creating high-level components with a generative representation for body-brain evolution,” Artificial Life, vol. 8, pp. 223–246, 2002.
G. S. Hornby, S. Takamura, O. Hanagata, M. Fujita, and J. Pollack, “Evolution of controllers from a high-level simulator to a high dof robot,” in Evolvable Systems: From Biology to Hardware; Proc. of the Third Intl. Conf., J. Miller (ed.), Lecture Notes in Computer Science; Springer, vol. 1801, 2000, pp. 80–89.
H. Kitano, “Designing neural networks using genetic algorithms with graph generation system,” Complex Systems, vol. 4, pp. 461–476, 1990.
J. R. Koza, Genetic Programming: On the Programming of Computers by Means of Natural Selection. MIT Press, Cambridge, MA, 1992.
J. R. Koza, F. H. Bennett III, D. Andre, and M. A. Keane, “Automated WYWIWYG design of both the topology and component values of analog electrical circuits using genetic programming,” in Genetic Programming 1996: Proceedings of the First Annual Conference, Stanford University, CA, USA, J. R. Koza, D. E. Goldberg, D. B. Fogel, and R. L. Riolo (eds.), MIT Press, 1996, pp. 123–131.
W. B. Langdon, “Size fair and homologous tree genetic programming crossovers,” in Proceedings of the Genetic and Evolutionary Computation Conference, Orlando, Florida, USA, W. Banzhaf, J. Daida, A. E. Eiben, M. H. Garzon, V. Honavar, M. Jakiela, and R. E. Smith (eds.), Morgan Kaufmann, 1999, vol. 2, pp. 1092–1097.
A. Lindenmayer, “Mathematical models for cellular interaction in development,” parts I and II. Journal of Theoretical Biology, vol. 18, 1968, pp. 280–299 and 300–315.
J. Lohn, D. Gwaltney, G. Hornby, R. S. Zebulum, D. Keymeulen, and A. Stoica (eds.). The 2005 NASA/DoD Conference on Evolvable Hardware, Washington, DC, IEEE Press, 2005.
S. Luke and L. Spector, “Evolving graphs and networks with edge encoding: Preliminary report,” in Late-breaking Papers of Genetic Programming 96, Stanford Bookstore, J. Koza (ed.), 1996, pp. 117–124.
J. P. Mermet (ed.) IEEE Standard VHDL Language Reference Manual, IEEE Std 1076-1993, Order Code SH 16840. The Institute of Electrical and Electronics Engineers, New York, NY, 1994.
J. F. Miller and P. Thomson, “A developmental method for growing graphs and circuits,” in Fifth Intl. Conf. on Evolvable Systems: From Biology to Hardware, A. M. Tyrrell, P. Haddow, and J. Torrensen (eds.), Lecture Notes in Computer Science; Springer, 2003, vol. 2606, pp. 93–104.
S. Nolfi and D. Floreano (eds.), Evolutionary Robotics. MIT Press, Cambridge, MA, 2000.
S. Nolfi and D. Parisi, “growing neural networks,” Technical Report PCIA-91-15, Institute of Psychology, CNR Rome, 1992.
S. Nolfi and D. Parisi, “Evolving artificial neural networks that develop in time,” in European Conference on Artificial Life, F. Morán, A. Moreno, J. J. Merelo, and P. Chacón (eds.), Springer, 1995, pp. 353–367.
R. Poli, “Evolution of graph-like programs with parallel distributed genetic programming,” in Proc. of the Seventh Intl. Conf. on Genetic Algorithms, San Mateo, California, E. Goodman (ed.), Morgan Kaufmann, 1997, pp. 18–25.
R. Poli and W. B. Langdon, “Schema theory for genetic programming with one-point crossover and point mutation,” Evolutionary Computation, 1998, vol. 6, pp. 231–252.
A. Siddiqi and S. Lucas, “A comparison of matrix rewriting versus direct encoding for evolving neural networks,” in IEEE International Conference on Evolutionary Computation, IEEE Press, Piscataway, NJ, 1998, pp. 392–397.
A. Witkin and D. Baraff, “Physically based modeling: Principles and practice,” Online Siggraph '97 Course notes, http://www-2.cs.cmu.edu/∼baraff/sigcourse/index.html.
R. S. Zebulum, D. Gwaltney, G. Hornby, D. Keymeulen, J. Lohn, and A. Stoica (eds.), The 2004 NASA/DoD Conference on Evolvable Hardware, Seattle, WA, IEEE Press, 2004.
Acknowledgments
Some of this research was conducted while the author was at Sony Computer Entertainment America, Research and Development as well as Brandeis University. The soccer game and simulator was developed by Eric Larsen at SCEA R&D.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by:
R. Poli
Rights and permissions
About this article
Cite this article
Hornby, G.S. Shortcomings with using edge encodings to represent graph structures. Genet Program Evolvable Mach 7, 231–252 (2006). https://doi.org/10.1007/s10710-006-9007-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10710-006-9007-5