Abstract
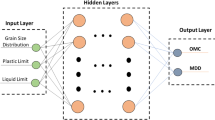
This paper presents Artificial Neural Network (ANN) prediction models which relate permeability, maximum dry density (MDD) and optimum moisture content with classification properties of the soils. The ANN prediction models were developed from the results of classification, compaction and permeability tests, and statistical analyses. The test soils were prepared from four soil components, namely, bentonite, limestone dust, sand and gravel. These four components were blended in different proportions to form 55 different mixes. The standard Proctor compaction tests were adopted, and both the falling and constant head test methods were used in the permeability tests. The permeability, MDD and optimum moisture content (OMC) data were trained with the soil’s classification properties by using an available ANN software package. Three sets of ANN prediction models are developed, one each for the MDD, OMC and permeability (PMC). A combined ANN model is also developed to predict the values of MDD, OMC, and PMC. A comparison with the test data indicates that predictions within 95% confidence interval can be obtained from the ANN models developed. Practical applications of these prediction models and the necessary precautions for using these models are discussed in detail in this paper.











Similar content being viewed by others
References
Blotz LR, Benson CH, Boutwell GP (1998) Estimating optimum water content and maximum dry unit weight for compacted clays. J Geotech Geo-Environ Eng, ASCE 124(9):907–912
Burmister DM (1954) Principles of permeability testing of soils. Astm symposium on permeability of soils. ASTM Spec Tech Publ 163:3–26
Carman PC (1937) Fluid flows through granular beds, Trans Inst Chem Engrs, London, England 15:150–166
Chen CY, Bullen AGR, Elnaggar HA (1977) Permeability and related principles of coal refuse. Trans Res Record 640:49–52
Davidson DT, Gardiner WF (1949) Calculation of standard proctor density and optimum moisture content from mechanical analysis, shrinkage factors, and plasticity index. Proceedings HRB 29:447–481
Garcia-Bengochea I, Lovell CW, Altschaeffl AG (1979) Pore distribution and permeability of silty gays. J Geotech Eng Div, ASCE 105(GT7):839–855
Gupta SC, Larson WE II (1979) A model for predicting packing density of soils using particles-size of distribution. Soil Sci Soc Am J 43(4):758–764
Hauser VL (1978) Seepage control by particle size selection. Trans Am Soc Agric Engrs 21(4):691–695
Haykin S (1994) Neural network: a comprehensive foundation. MacMillan Publication
Hazen A (1911) Discussion of dams on sand foundations. Trans ASCE 73:199–203
Horn ME (1971) Estimating soil permeability rates. J Irrigation Drain Div, ASCE 97(IR2), June:263–274
Hornik K (1993) Some New Results on Neural Network Approximation. Neural Netw 6:1069–1072
Jumikis AR (1946) Geology and soils of the Newark (N.J.) metropolitan area. J Soil Mech Found Div, ASCE 93(SM2):71–95
Lambe TW (1951) Soil testing for engineers. John Wiley and Sons, Inc, New York, NY
Lambe TW (1954) The permeability of fine grained soils. ASTM Special Technical Publication 163:123–126
Linveh M, Ishai I (1978) Using indicative properties to predict the density-moisture relationship of soil. Trans Res Record (60P):22–28
Lippmann RP (1987) An introduction to computing with neural nets. IEEE ASSP Magazine 4:4–22
Michaels AS, Lin CS (1954) The permeability of kaolinite. Ind Eng Chem 46:1239–1246
Mitchell JK, Hopper DR, Campanella RC (1965) Permeability of compacted clay. J Soil Mech Found Div, ASCE 91(SM4):41–65
NeuralWare, User’s and Reference Guide (2001) Professional II/Plus. Carnegie, Pennsylvania
Olson RE (1963) Effective stress theory of soil compaction. J Soil Mech Found Div, ASCE 89(SM2):27–45
Ramiah BK, Viswanath V, Krishnamurthy HV (1970) Interrelationship of compaction and index properties. Proceedings, Second Southeast Asian Conference on Soil Engineering, Singapore 577–587
Ring GW, Sallgerb JR, Collins WH (1962) Correlation of compaction and classification test data. HRB Bulletin 325:55–75
Rowan HW, Graham WW (1948) Proper compaction eliminates curing period in construction fills. Civil Eng 18:450–451
Rumelhart D, Hinton G, Williams R (1986) Learning representations by backpropagation Errors, Parallel distributed processing vol 1. MIT Press, Cambridge Mass, pp 318–362
Schmidt WF (1993) Initialization, backpropagation, and generalization of feedforward classifier. IEEE Int Conf on Neural Networks 598–604
Taylor DW (1948) Fundamentals of soil mechanics. John Wiley and Sons, Inc, NY
Turnbull JM (1948) Computation of the optimum moisture content in the moisture-density relationship of soils. Proceedings, Second International Conference on Soil Mechanics and Foundation Engineering, Rotterdam, Holland, vol IV, pp 256–262
Wang MC, Huang CC (1984) Soil compaction and permeability prediction models. J Environ Eng, ASCE 110(6):1063–1083
Zunker F (1930) Das Verhalten des Bodens Zum Wasser. Handbuch der Bodenlehre 6:66–220
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Sinha, S.K., Wang, M.C. Artificial Neural Network Prediction Models for Soil Compaction and Permeability. Geotech Geol Eng 26, 47–64 (2008). https://doi.org/10.1007/s10706-007-9146-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10706-007-9146-3