Mode I fatigue limit of notched structures: A deeper insight into Finite Fracture Mechanics

Abstract

In the present contribution, the coupled stress-energy criterion of Finite Fracture Mechanics (FFM) is applied to assess the fatigue limit of structures weakened by sharp V- and U-notches and subjected to mode I loading conditions. The FFM is a critical-distance-based approach whose implementation requires the knowledge of two material properties, namely the plain material fatigue limit and the threshold value of the stress intensity factor (SIF) range for the fatigue crack growth of long cracks. However, the FFM critical distance is a structural parameter, being a function not only of the material but also of the geometry of the notched component. Experimental notch fatigue results taken from the literature and referred to a variety of materials and geometrical configurations are compared with FFM theoretical estimations, obtained through simple semi-analytical relationships. The case of semi-circular edge notches is also dealt with.

1 Introduction

The presence of cracks or notches in a structural component gives rise to a local stress concentration, which could result in a reduction of the load-carrying capacity of the component both under static and cyclic loading conditions. Accordingly, reliable approaches must be provided to design engineers in order to evaluate if such a component is working under safe conditions. Dealing with structures weakened by cracks or notches and subjected to cycling loading conditions, two different concepts have been adopted in the technical literature to assess their fatigue strength behaviour:

• the stress concentration factor K$_{{tg}}$ according to the local peak stress approach for components weakened by blunt notches (Neuber 1958; Peterson 1959);

• the stress intensity factor (SIF) $K_{{I}}$ according to the Linear Elastic Fracture Mechanics (LEFM) approach for components containing cracks (Kitagawa and Takahashi 1976; Smith and Miller 1978; Atzori et al. 2001, 2003); or, more in general, the extended concept of notch stress intensity factor (NSIF) $K_{\mathrm {I }}^{{V}}$ according to Linear Elastic Notch Mechanics (LENM) in the case of sharp V-notches (Kihara and Yoshii 1991; Boukharouba et al. 1995; Atzori et al. 2005).

The approach based on the stress concentration factor ${K}_{{tg}}$ is suitable for blunt notches, whereas it does not provide an effective estimation of the fatigue strength in the case of defects or when dealing with cracked or sharp V-notched components. On the other hand, the SIF and NSIF approaches allow to properly assess the fatigue strength of structures weakened by long cracks or sharp-notches, respectively. Indeed, they are not effective in the cases of short features, for which they provide an overestimated fatigue strength, and of blunt notches, for which, on the contrary, they provide an underestimated fatigue strength.

Many contributions in the literature were devoted to provide a unified approach able to assess the fatigue limit of structural components weakened by any of the common stress raisers (defects, cracks, sharp and blunt notches), therefore covering both LEFM, LENM, as well as the notch mechanics. In this framework, the first investigation was performed by (Frost 1957; Frost et al. 1974; Smith and Miller 1978), who derived a link between the notch mechanics and the LEFM by analysing the fatigue limit of U-notched plates under pure mode I, where the notch tip radius R was varied while keeping constant the notch depth a. Later on, Atzori et al. (2001) analysed the fatigue limit of centrally U-notched plates under pure mode I by varying the notch depth a while keeping constant the notch acuity $\zeta = a/R.$ Doing so, they were able to provide a generalization of the Kitagawa and Takahashi diagram (Kitagawa and Takahashi 1976) which accounts not only for the defect sensitivity, but also for the notch sensitivity. Subsequently, Atzori et al. (2005) extended the diagram also to V-notches, providing a unified treatment which encompasses the fatigue limit relevant to stress raisers of different size, opening angle and notch tip radius. Finally, it is worth mentioning that the Atzori-Lazzarin diagram was extended to estimate the fatigue limit of notched components under torsion (mode III) loading in (Atzori and Meneghetti 2006), and also under multiaxial (mode $\hbox {I}+\hbox {III}$) loading conditions in (Atzori and Susmel 2005). The fatigue behaviour of structures weakened by either cracks or notches has treated through a unified approach also by Tanaka (1983), who proposed a method based on LEFM parameters; by Taylor (1999), who put forward the Theory of Critical Distances (TCD); and by Lazzarin and collaborators (Lazzarin and Zambardi 2001; Berto and Lazzarin 2009), who proposed the averaged strain energy density (SED) approach.

The TCD (Taylor 1999) is a group of methodologies which includes the point method (PM) as the simplest approach. The PM requires to calculate the range of the maximum principal stress at a distance from the notch tip $l_{c,PM} =\frac{1}{2\pi }\left( {\frac{\Delta K_{th} }{\Delta \sigma _{0} }} \right) ^{2}=\frac{a_{0} }{2}$, $a_{\mathrm {0}}$ being the El Haddad-Smith-Topper parameter (El Haddad et al. 1979). Then, the considered notched component reaches the fatigue limit condition when the calculated stress is equal to the plain material fatigue limit, $\Delta \sigma _{\mathrm {0}}$. In the same context, another widely employed criterion is the line method (LM), which is based on the averaging of the maximum principal stress along the critical distance $l_{c,LM} =\frac{2}{\pi }\left( {\frac{\Delta K_{th} }{\Delta \sigma _{0} }} \right) ^{2}=2a_{0}$ from the notch tip. According to the LM, the fatigue limit of a notched component occurs when the average stress range equals $\Delta \sigma _{\mathrm {0}}$. Dealing with the sharp V-notch geometry of Fig. 1, the PM and the LM criteria can be expressed by Eqs. (1) and (2), respectively:

$$\begin{aligned}&\Delta \sigma _{y} \left( {x=l_{c,PM} } \right) =\Delta \sigma _{0} \end{aligned}$$

(1)

$$\begin{aligned}&\frac{1}{l_{c,LM} }\int \limits _0^{l_{c,LM} } {\Delta \sigma _{y} \left( x \right) dx} =\Delta \sigma _{0} \end{aligned}$$

(2)

Many contributions in the literature (Atzori and Lazzarin 2001; Taylor 2007; Susmel 2008; Susmel and Taylor 2011) were devoted to investigate which of the two previous approaches, i.e. PM and LM, allows to obtain the best accurate predictions on experimental results. However, the choice depends on the analysed case and, in particular, on the geometry of the notched component, as discussed in (Livieri and Tovo 2004; da Silva et al. 2012; Beber et al. 2019).

Fig. 1

(a) semi-infinite V-notched plate, and (b) infinite V-notched plate under tensile load

It is worth noting that stress-based criteria, such as PM and LM according to Eqs. (1) and (2), could fail in predicting the fatigue strength of a notched or cracked structure having size comparable to the critical distance $l_{c}$. This occurs due to the assumption that the TCD critical distance $l_{c}$ is just a material constant. To overcome this issue, a coupled stress-energy approach, the so-called Finite Fracture Mechanics (FFM), was proposed by Leguillon (2002) and Cornetti et al. (2006), and it has been widely adopted for the static strength assessment of cracked or notched structures. Differently from stress based approaches (PM and LM), FFM has a straightforward generalization to model complex geometries such as interfacial cracks (Muñoz-Reja et al. 2016) or cavities under pressure, to cite but a few. Furthermore, FFM provides close predictions to the powerful Cohesive Zone Model both as concerns the failure load and the finite crack advancement, once the cohesive law is properly defined (Cornetti et al. 2019; Doitrand et al. 2019). Among the recent FFM developments, let us cite the treatment of quasi-brittle or hyperelastic materials (Leguillon and Yosibash 2017; Rosendahl et al. 2019), and the investigation of 3D crack propagation (Doitrand and Leguillon 2018; Cornetti and Sapora 2019).

The FFM approach proposed by Cornetti et al. (2006), for instance, considers as stress-based condition that corresponding to the LM according to Eq. (2). Furthermore, the energy-based condition states that failure happens if the average crack driving force equals the crack resistance, i.e. the so-called fracture energy (Carpinteri et al. 2008). When dealing with fatigue loadings applied to a linear elastic material, the energy-based condition can be extended to the fatigue limit by introducing the J-integral range concept (Sapora et al. 2020):

$$\begin{aligned} \frac{1}{l_{c} }\int \limits _0^{l_{c} } {\Delta J(c)dc} =\Delta J_{th} \end{aligned}$$

(3)

In previous expression, c represents the length of a crack stemming from the feature tip, i.e. either a pre-existing crack or a notch. Taking advantage of the relationship between the J-integral range and the SIF range according to (Anderson 2009), Eq. (3) can be re-written in the following fashion:

$$\begin{aligned} \frac{1}{l_{c} }\int \limits _0^{l_{c} } {\Delta K_{I}^{2} (c)dc} =\Delta K_{th}^{2} \end{aligned}$$

(4)

$\Delta \,K_{{th}}$ is assumed as the critical value for the FFM energy condition applied to the fatigue limit (see also (Sapora et al. 2020)), since $\Delta \,K_{{th}}$ is the threshold value of the mode I SIF range, above which propagation of long cracks occurs according to Paris’ law. Moreover, it is worth noting that the reformulation of the energy-based condition applied to the fatigue limit - under linear elastic condition - in terms of SIF range is in agreement also with the SED approach proposed by (Lazzarin and Zambardi 2001).

The FFM generalization to the fatigue limit condition can be thus expressed by a system of two equations, i.e. Eqs. (2) and (4), with two unknowns: the critical crack advance $l_{c},$ which becomes a structural parameter (function of both the material and the geometry of the structure), and the fatigue strength $\Delta \sigma _{f}$. The FFM criterion based on the coupling of Eqs. (2) and (4) has been recently applied to predict the fatigue limit of mechanical components subjected to tensile loading conditions and weakened by a central sharp crack or a circular hole (Sapora et al. 2019, 2020), thus focusing on the crack/notch sensitivity. It is worth noting that the first application of FFM to the fatigue strength assessment of notched components was performed independently both in (Sapora et al. 2019, 2020) and in (Liu et al. 2020). Afterwards, the aims of the present contribution are:

• to estimate the fatigue limit of structures weakened by sharp V-notches or U-notches and subjected to mode I loadings by applying the coupled criterion of Finite Fracture Mechanics.

• to validate the approach against experimental notch fatigue results taken from the literature and referred to a variety of materials and geometrical configurations.

2 Sharp V-notched structures

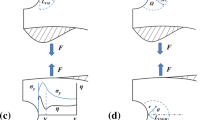
When dealing with the structural behaviour of V-notched elements, the notch stress intensity factor (NSIF) $K_{I}^{V}$ represents the coefficient of the dominant term of the stress field at the notch tip and it is defined by Eq. (5), which includes the opening stress component $\sigma _{y}(x)$ calculated along the notch bisector line ($y = 0$, see Fig. 1):

$$\begin{aligned} K_{I}^{V} =\lim \limits _{_{x\rightarrow 0} } \left[ {\sigma _{y} \left( x \right) \cdot \left( {2\pi x} \right) ^{1-\lambda }} \right] \end{aligned}$$

(5)

Indeed, $K_{I}^{V}$ can be reasonably assumed as the governing failure parameter within brittle structural behaviour. The fatigue limit condition under mode I loading conditions is thus expressed as:

$$\begin{aligned} \Delta K_{I}^{V} =\Delta K_{I,th}^{V} \end{aligned}$$

(6)

$\Delta K_{I,th}^{V}$ being the threshold range of the NSIF.

Table 1 Values of the parameters implemented in the present analysis as a function of the notch amplitude

In cases of a semi-infinite V-notched slab (a being the notch depth) or an infinite center V-notched slab (i.e. with a rhombus hole, a being the half notch depth) under uniaxial remote tension $\Delta \sigma$ (Fig. 1), we have that

$$\begin{aligned} \Delta K_{I}^{V} (a)=\beta (\omega )a^{1-\lambda }\Delta \sigma \end{aligned}$$

(7)

The shape functions $\beta$ related to the two geometries under investigation were evaluated by Dunn et al. (1997) and, together with the well-known William’s eigenvalues $\lambda ,$ they are reported in Table 1 for different notch amplitudes $\omega$. The values of $\beta$ differ by a factor 1.12 for the crack case ($\omega = 0^{\circ }$, $\Delta K_{I}^{V} =\Delta K_{I} =\beta \sqrt{a} \Delta \sigma$), while they coincide for the unnotched geometry ($\omega = 180^{\circ }$ , $\beta = 1$, $\Delta K_{I}^{V} =\Delta \sigma$).

By referring to the frame of reference in Fig. 1, we can rewrite the coupled FFM criterion expressed by Eqs. (2) and (4), as:

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{1}{l_{c} }\int \limits _0^{l_{c} } {\Delta \sigma _{y} \left( x \right) dx} =\Delta \sigma _{0} \\ \frac{1}{l_{c} }\int \limits _0^{l_{c} } {\Delta K_{I}^{2} (c)dc} =\Delta K_{th}^{2} \\ \end{array}} \right. \end{aligned}$$

(8)

In order to implement Eq. (8), the stress field and the SIF are needed. The first function can be approximated by the asymptotic relationship

$$\begin{aligned} \Delta \sigma _{y} (x)=\frac{\Delta K_{I}^{V} }{\left( {2\pi x} \right) ^{1-\lambda }} \end{aligned}$$

(9)

whereas the second through the expression proposed by (Hasebe and Iida 1978):

$$\begin{aligned} \Delta K_{I} (c)=\mu (\omega )\Delta K_{I}^{V} c^{\lambda -0.5} \end{aligned}$$

(10)

The parameter $\mu$ increases from unity, when $\omega =$ 0°, up to 1.12 $\surd \pi$, when Eq. (10) coincides with the formula for the SIF of an edge crack $(\omega = 180^{\circ })$. Accurate values can be found in tabulated form in (Livieri and Tovo 2009) and they are reported in Table 1 (according to the present definition of the NSIF $K_{I}^{V}$, Eq. (5)), for the sake of completeness.

Table 2 Functions $\xi$ and $\psi$ according to different criteria based on a critical distance

By introducing the threshold length

$$\begin{aligned} l_{th} =\left( {\frac{\Delta K_{th} }{\Delta \sigma _{0} }} \right) ^{2} \end{aligned}$$

(11)

the substitution of Eqs. (9) and (10) into system (8) yields:

$$\begin{aligned} \Delta K_{I,th}^{V} =\xi (\omega )l_{th}^{2(1-\lambda )} \Delta \sigma _{0} \end{aligned}$$

(12)

where

$$\begin{aligned} \xi (\omega )=\lambda ^{\lambda }\left[ {\frac{\left( {2\pi } \right) ^{2\lambda -1}}{\mu ^{2}/2}} \right] ^{1-\lambda } \end{aligned}$$

(13)

and

$$\begin{aligned} l_{c} =\psi (\omega )l_{th} \end{aligned}$$

(14)

where

$$\begin{aligned} \psi (\omega )=\frac{2}{\lambda \mu ^{2}\left( {2\pi } \right) ^{2(1-\lambda )}} \end{aligned}$$

(15)

Indeed, for approaches based on a critical distance it has been proved that Eqs. (12) and (14) still hold true (Lazzarin and Zambardi 2001; Atzori et al. 2005; Carpinteri et al. 2008, 2010), but for a different definition of the functions $\xi$ and $\psi$, which depend on the criterion under investigation. Table 2 summarizes the results for different criteria: the point method (PM, Eq. (1)) and the line method (LM, Eq. (2)) by (Taylor 2007), the generalized LEFM (Atzori et al. 2005), and the quantized fracture mechanics, QFM (Pugno and Ruoff 2004). The functions $\xi$ are plotted in Figure 2, showing very close values within the range $0^{\circ } \leqslant \omega < 90^{\circ }$ , all the values being comprised within 2%, and the maximum deviations for $\omega \cong 145^{\circ }$. Note that all the criteria involve a constant crack advance $l_{c}$ ($\psi$ being constant in Table 2), whereas it results a structural parameter for the FFM approach (Eq. (15)). Its values lay between $2/\pi$ for the cracked case $(\omega = 0^{\circ })$ to $2/(1.12^{\mathrm {2}}\pi )$ for the un-notched geometry $(\omega = 180^{\circ })$. In the former case, the problem is assessed by LEFM ($\Delta K_{I} = \Delta K_{th})$: the energy balance in (8) is self-consistent to get the fatigue limit, and the FFM stress requirement provides the value of $l_{c}$ (coinciding with that by the LM). In the latter case, the problem is stress governed $(\Delta \sigma _{f}=\Delta \sigma _{\mathrm {0}})$, and the FFM energy condition furnishes the value of $l_{c}$ (corresponding to that of QFM).

Fig. 2

V-notches: $\xi$ function according to different criteria based on a critical distance

Fig. 3

V-notches: FFM generalized Kitagawa and Takahashi diagram for different notch amplitudes $\omega$. The dotted line refers to predictions by Eq. (17). In the lower-left box a zoom on the intersection points of curves by Eq. (16) is depicted

Upon substitution of Eqs. (7) and (12) into the fatigue limit condition (6), one gets:

$$\begin{aligned} \frac{\Delta \sigma _{f} }{\Delta \sigma _{0} }=\frac{\xi }{\beta \,\bar{{a}}^{1-\lambda }}=\frac{\xi }{\left( {\beta ^{\frac{1}{^{1-\lambda }}}\bar{{a}}} \right) ^{^{1-\lambda }}} \end{aligned}$$

(16)

where $\bar{{a}}=a/l_{th}$ is the dimensionless notch depth.

Table 3 Material properties implemented in the present analysis (R represents the loading ratio)

Equation (16) can be modified to take short notches into account by inserting a parameter $\bar{{a}}_{0}^{V}$ in order to recover $\Delta \sigma _{f} \rightarrow \Delta \sigma _{0}$ as $a\rightarrow 0$, similarly to what proposed by (Atzori et al. 2005). In formulae:

$$\begin{aligned} \frac{\Delta \sigma _{f} }{\Delta \sigma _{0} }=\frac{\xi }{\left( {\beta ^{\frac{1}{^{1-\lambda }}}\bar{{a}}+\bar{{a}}_{0}^{V} } \right) ^{1-\lambda }} \end{aligned}$$

(17)

where $\bar{{a}}_{0}^{V} =\xi ^{\frac{1}{1-\lambda }}$. By looking at the expressions for $\xi$ reported in Table 1 (see also Fig. 2), $\bar{{a}}_{0}^{V}$ is constant according to the PM, whereas it generally results a monotonic increasing function in $\omega$ for the other criteria. It is worth noting that the analysis derived here differs from that reported in (Atzori et al. 2005) not only for the fatigue approach adopted, but also for the definition of the NSIF according to both Eqs. (5) and (7).

Predictions according to Eqs. (16) and (17) are reported in Fig. 3 for increasing notch amplitudes $\omega$, leading to the so-called generalized Kitagawa and Takahashi diagram for V-notches.

For finite geometries, the analysis presented above still holds true, but for the shape function $\beta$ in Eq. (7), whose values are no longer those tabulated in Table 1. Indeed, they refer to the particular structure under investigation (depending on the notch amplitude, the geometry and the size of the notched component), and must be generally evaluated through a FEA. It has recently been demonstrated in (Meneghetti et al. 2016) that shape functions can be rapidly estimated by using sharp and coarse FE models thanks to the Peak Stress Method (PSM), which was originally proposed by Meneghetti and Lazzarin (2007). On the other hand, mesh requirements for the numerical implementation of FFM have been discussed by Doitrand et al. (2020). By considering the shape functions estimated in (Atzori et al. 2005) and there termed $\alpha _{\mathrm {\gamma }}$, with $\beta =\frac{\alpha _{\gamma } \sqrt{\pi }}{\left( {2\pi } \right) ^{\lambda -0.5}}$ according to the present notation, we can apply FFM to the experimental tests carried out by Kihara and Yoshii (1991) on HT60 class high strength steel and SS41 class mild steel, respectively. The material properties of these two materials are reported in Table 3. As concerns the data related to $135^{\circ }$ and $150^{\circ },$ they refer to cruciform specimens idealizing welded joints. In this case, a (and the corresponding shape function $\beta$) refers to the joint thickness. The comparison is presented in Fig. 4 revealing a good agreement.

Fig. 4

V-notched elements: fatigue limit according to FFM and experimental data from (Kihara and Yoshii 1991) for different notch amplitudes $\omega$

3 U-notched structures

Let us now consider a U-notched geometry (Figure 5), which has already been treated by Sapora and Firrao (2017) in the FFM framework.

Fig. 5

(a) U-notched and (b) semi-circular notched geometries

For sufficiently slender notches, the stress field can be approximated by means of (Creager and Paris 1967) relationship:

$$\begin{aligned} \Delta \sigma _{y} (x)=\frac{2\Delta K_{I}^{U} }{\sqrt{\pi }}\frac{x+R}{(2x+R)^{3/2}} \end{aligned}$$

(18)

which provides errors less than 4% as $x< R/2$, and then it overestimates the real stress field.

On the contrary, the SIF can be expressed through the expression proposed by Sapora et al. (2014):

$$\begin{aligned} \Delta K_{I} (c)=\left\{ {1+\left[ {\frac{R}{5.02c}} \right] ^{n}} \right\} ^{-\,\frac{1}{2n}}\Delta K_{I}^{U} \end{aligned}$$

(19)

provided that the length c is much smaller than the notch depth a. In case of a crack as the present one, the fitting parameter n was estimated equal to 1.82 by means of a FEA, and the maximum percentage error is below 1%.

In Eqs. (18) and (19) $K_{I}^{U}$ represents the apparent SIF, which can be expressed as a function of the applied stress (Glinka 1985):

$$\begin{aligned} \Delta K_{I}^{U} =Y\Delta \sigma \sqrt{\pi a} =\Delta \sigma \sqrt{\pi \left( {Y^{2}a} \right) } \end{aligned}$$

(20)

the shape factor Y depending on the geometry under consideration.

By introducing the notch acuity $\zeta =a/R$ and keeping it fixed, substituting Eqs. (18) and (19) into the FFM system (8) yields two coupled equations. At fatigue limit condition, after some manipulations we get:

$$\begin{aligned}&\frac{l_{c} }{2Y^{2}a}+\frac{1}{4Y^{2}\zeta }\nonumber \\&\quad =\frac{l_{c} l_{th} }{\pi \left( {Y^{2}a} \right) ^{2}}\left( {\int \limits _0^{l_{c} /Y^{2}a} {\frac{1}{\left[ {1+\left( {\frac{1}{5.02Y^{2}\zeta t}} \right) ^{1.82}} \right] ^{\frac{1}{1.82}}}} dt} \right) ^{-1} \end{aligned}$$

(21)

which is an implicit equation providing the crack advance $l_{c}$, and

$$\begin{aligned} \frac{\Delta \sigma _{f} }{\Delta \sigma _{0} }=\sqrt{\frac{l_{c} }{2Y^{2}a}+\frac{1}{4Y^{2}\zeta }} \end{aligned}$$

(22)

which allows one to estimate the fatigue strength, once $l_{c}$ is known from Eq. (21).

Fig. 6

U-notches: FFM crack advance referring to different values $Y^{\mathrm {2}}\zeta =$ 5, 10, 25, 50 and 100

The dimensionless crack advance $\bar{{l}}_{c} =l_{c} /l_{th}$ is plotted in Fig. 6, for different $\zeta$ values. For very large notch sizes a, the notch tip radius R is large too ($\zeta =a/R$ being constant for each curve). The fatigue limit $\Delta \sigma _{f}$ can be estimated by the range of the peak stress at the notch tip: $\Delta \sigma _{f}=\Delta \sigma _{\mathrm {0}}/K_{tg}$, $K_{tg}=2\surd \zeta$ being the stress concentration factor related to the gross section. The FFM solution is thus stress-governed, and the energy condition defines the crack advance, which coincide with that related to QFM (Table 1). On the other hand, as the size a decreases (and the radius R as well), the notch is equivalent to a long crack of the same size and, therefore, the fatigue limit is dictated by LEFM: $\Delta K_{I} = \Delta K_{th}$. The fatigue limit according to FFM is energy driven, and the stress condition defines the crack advance, which coincides with that related to LM (Table 1). Fatigue limit predictions are presented in Fig. 7, together with experimental results related to different geometries and metallic materials: 0.45 Carbon steel and 0.36 Carbon steel (Nisitani and Endo 1988), Mild steel (Harkegard 1981), FeP04 steel and AA 356-T6 Cast Al alloy (Lazzarin et al. 1997). Their properties are reported in Table 3, for the sake of completeness, whereas sample details are summarized in Table 2 of (Atzori et al. 2005). The matching between FFM results and experimental data reveals again satisfactory.

Fig. 7

U-notches: comparison between experimental data from (Harkegard 1981; Nisitani and Endo 1988; Lazzarin et al. 1997) and FFM predictions referring to different acuities; from the top to the bottom curves refer to $Y^{2}\zeta =$ 5, 10, 25, 50 and 100

4 Semi-circular notches

Finally, let us consider the case of a semi-circular notch with radius $R=a$ (Fig. 5b). If a is small enough with respect to the other geometrical dimensions, the stress field ahead of the notch tip can be approximated by (Usami 1987):

$$\begin{aligned} \Delta \sigma _{y} (x)=\frac{\Delta \sigma K_{tg} }{3}\left[ {1+\frac{1}{2}\frac{a^{2}}{\left( {x+a} \right) ^{2}}+\frac{3}{2}\frac{a^{4}}{\left( {x+a} \right) ^{4}}} \right] \end{aligned}$$

(23)

On the other hand, despite some studies were performed in the past (e.g., (Lin and Hills 1996)), a new relationship is here put forward for the SIF (necessary for the second FFM condition, Eq. (8)), for the sake of simplicity. The expression reads:

$$\begin{aligned} \Delta K_{I} (c)=Y(s)\Delta \sigma \sqrt{\pi c\,} \end{aligned}$$

(24)

where

$$\begin{aligned} s=\frac{c}{c+a} \end{aligned}$$

(25)

and

$$\begin{aligned} Y(s)=\frac{1.12K_{tg} }{\left[ {1-s+\left( {\sqrt{s} K_{tg} } \right) ^{\frac{1}{n}}} \right] ^{n}} \end{aligned}$$

(26)

The relationship proposed above fulfils the asymptotic limits of a short crack (which corresponds to an edge crack subjected to the local peak stress):

$$\begin{aligned} Y(s)=1.12K_{tg} \end{aligned}$$

(27)

and a long crack (which corresponds to an edge crack of length $c+a)$

$$\begin{aligned} Y(s)=\frac{1.12}{\sqrt{s} } \end{aligned}$$

(28)

By considering $K_{tg}= 3.065$, i.e. the stress concentration factor related to a semi-circular notch in a semi-infinite tensile plate, the parameter n is estimated equal to 0.29 through a FEA using least squares estimation. Results are presented in Fig. 8: the maximum percentage discrepancy is around 2%.

Fig. 8

Dimensionless SIF vs. dimensionless crack length: predictions according to Eq. (24) with $n=0.29$ and numerical data

Substituting Eqs. (23) and (24) into the FFM system (8) yields again two coupled equations:

$$\begin{aligned} \frac{\Delta \sigma _{f} }{\Delta \sigma _{0} }= & {} \frac{3}{K_{tg} }\frac{2\left[ {1+\left( {l_{c} /a} \right) } \right] ^{3}}{2\left( {l_{c} /a} \right) ^{3}+8\left( {l_{c} /a} \right) ^{2}+11\left( {l_{c} /a} \right) +6}\nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned} \frac{\Delta \sigma _{f} }{\Delta \sigma _{0} }= & {} \sqrt{\frac{l_{c} l_{th} }{\pi a^{2}}\frac{1}{\int _0^{l_{c} /a} {tY^{2}(t=c/a)dt} }} \end{aligned}$$

(30)

Equalling the right hand sides of Eqs. (29) and (30) yields an implicit equation in $l_{c}$. Once solved, this value is inserted either in Eq. (29) or in Eq. (30) to get the dimensionless fatigue limit $\Delta \sigma _{f}$. Let us remark that, due to the approximation introduced by Eq. (23), it follows that $\Delta \sigma _{f} /\Delta \sigma _{0} \rightarrow 0.98$ as the radius a vanishes (see Eq. (29)).

Fig. 9

Semi-circular notches: FFM predictions (thick line) and experimental data (Harkegard 1981; Nisitani and Endo 1988; Lazzarin et al. 1997). The thin line refers to FFM results concerning an edge crack with a length equal to the notch radius, the dot-dashed line refers to LEFM predictions

The experimental results presented in (Atzori et al. 2005), together with FFM predictions, are reported in Fig. 9, showing a good agreement. Indeed, a more detailed analysis can be performed by considering also the case of a sharp edge crack of length a (see the Appendix A for details on the FFM analysis), similarly to what presented in (Sapora et al. 2020). In particular, three ranges can be identified by the notation $\bar{{a}}=a/l_{th}$ (Fig. 9): if $\bar{{a}}>\bar{{a}}_{2}$ the structure is feature sensitive: the differences of a notch from a crack are consistent, and they increase as the size increases. As a matter of fact, for sufficiently long cracks, the failure behaviour of cracked elements is fully assessed by LEFM; if $\bar{{a}}_{1}<\bar{{a}}<\bar{{a}}_{2}$ the structure can be supposed to be shape insensitive, i.e. the strength is affected by the presence of a flaw, but regardless its geometry; if $\bar{{a}}<\bar{{a}}_{1}$ the structure is feature insensitive: the fatigue limit is not affected by the presence of a defect. By considering the present geometries and fixing an engineering tolerance of 5%, the following estimations can be provided: $\bar{{a}}_{1} \cong 0.018$ and $\bar{{a}}_{2} \cong 0.48$. Note that these values are lower than the corresponding ones obtained for central features (Sapora et al. 2020).

5 Conclusions

In the present contribution, the FFM criterion, which had been widely employed to the static strength assessment of brittle materials, was extended to predict the fatigue limit of structures weakened by sharp V-notches or U-notches under mode I loadings. The FFM is a critical-distance-based criterion which involves the simultaneous fulfilment of a stress-based and an energy-based condition, resulting in a system of two equations in two unknowns, i.e. the critical distance, which becomes a structural parameter, and the notch fatigue limit. The FFM approach was validated against experimental notch fatigue limits taken from the literature and involving several materials and notch geometries, having different notch opening angles and acuities. A good agreement between theoretical estimations and experimental results was observed. Finally, the problem of crack/notch sensitivity treated in (Sapora et al. 2020) for center features is extended to edge defects.

Appendix A

Let us consider the edge crack geometry (Fig. 5a, $R=0$). The stress field ahead of the crack tip can be approximated as (Sapora et al. 2020):

(A.1)

where the SIF threshold is given by $\Delta K_{I} (c)=Y\Delta \sigma \sqrt{\pi (a+c)\,}$ with $Y = 1.12$. A straightforward substitution into the FFM system (8) yields the following energetic condition

$$\begin{aligned} \frac{\Delta \sigma _{f} }{\Delta \sigma _{0} }\;=\sqrt{\frac{2}{\pi }\frac{l_{th} }{l_{c} (Y^{2}+2Y^{2}a/l_{c} )}} \end{aligned}$$

(A.2)

and the subsequent stress requirement

(A.3)

Equations (A.2) and (A.3) must be coupled together to get the FFM solution plotted in Fig. 9.