The effect of residual stress on a centre-cracked plate under uniaxial loading

Abstract

The behaviour of a crack in the centre of a plate subject to a far-field applied stress perpendicular to the crack surface has been studied. The plate contains an initial, self-equilibrated residual stress, symmetric to the central position of the crack. The component of the residual stress perpendicular to the crack at the centre of the plate can be tensile or compressive. Elastic and elastic–plastic material behaviours have been considered and crack closure effects have been included in the analyses. For elastic behaviour a series of analyses based on stress intensity factor solutions have been developed to calculate the crack opening and the stress intensity factor for cracks of different lengths relative to the size of the residual stress field. Different magnitudes of applied stress relative to the magnitude of the residual stress were applied. Crack behaviour maps have been developed that show the behaviour of the crack for different crack lengths and magnitudes of applied stress. For elastic–plastic behaviour a strip yield model has been used to develop a similar set of analyses to those for the elastic case. The results compare favourably with those produced by finite element analysis. The work provides the basis for a first estimate of the likelihood of fracture for a component containing residual stress and subject to applied load.

1 Introduction

In an engineering component containing a crack, residual stresses interact with stresses generated by applied loading in a complex manner. Typically, numerical techniques are required to predict the likelihood of fracture, providing results that are particular to the set of conditions considered. The work we describe here represents an attempt to understand the general behaviour of the crack for a simple geometry, loading and residual stress distribution that provides insight into the results of more complex analyses.

In general, a residual stress distribution is characterised by the magnitude and location of the peak residual stress and the spatial extent of its distribution. As an example, consider the as-welded residual stresses generated by a butt-weld between two identical plates. The magnitude of the peak residual stresses depends on the welding parameters and the material properties, including the phase transformation behaviour. Assuming symmetry the in-plane location of the peak residual stress is the centreline of the weld. Finally, the spatial extent of the residual stress distribution depends on the geometry of the weld and the thickness of the plates. We now introduce a through-thickness crack into the plate, symmetric about the weld centreline and subject the plate to a uniaxial applied stress in the direction parallel to the weld centreline. When the crack length is large compared to the extent of the residual stress distribution, the residual stress can be neglected, and a fracture analysis based only on the magnitude of the applied stress. Conversely, when the crack length is small compared to the extent of the residual stress distribution, the fracture analysis must use the sum of the residual stress and applied stress. When the crack length is similar to the extent of the residual stress distribution the analysis is more difficult: the crack is subject to stresses that vary with position and may in general cause parts of the crack surface to be in contact.

Terada (1976) provided an early analysis of the effect of residual stress on a crack. He proposed a residual stress distribution to represent a butt-weld between two plates and then developed a method to evaluate the stress intensity factor assuming elastic behaviour. Tada and Paris (1983) extended Terada’s analysis to different residual stress distributions and provided an alternative method to evaluate the stress intensity factor. Terada and Najajima (1985) considered a crack asymmetrically located within the residual stress field. Chell and Ewing (1977) discussed the effect of plasticity on fracture when residual stresses exist. Wu and Carlsson (1984) calculated stress intensity factors for half-elliptical surface cracks in residual stress fields demonstrating the non-conservatism of two-dimensional analyses. Labeas and Diamantakos (2009) used finite element analysis to explore the stress intensity factor for a crack of varying length embedded in a residual stress field. Bouchard and Withers (2006) and Bouchard et al. (2012) used a Fourier approach to study the influence of the size of the residual stress distribution on the stress intensity factor. In general, previous work has not explored the behaviour of the crack as the magnitude and spacial extent of the residual stress has been varied and therefore has been unable to draw general conclusions about the behaviour of the crack.

In this paper we investigate the behaviour of a crack in an infinite two-dimensional plate with an initial residual stress distribution under superimposed uniaxial tension. First, we describe our method for generating a residual stress distribution using a stress function. Next, we use existing stress intensity factor solutions to explore the linear elastic behaviour of the crack as the length of the crack relative to the size of the residual stress field is altered and the magnitude of the applied stress is increased. Maps are developed that show the behaviour of the crack for different magnitudes of applied stress and crack size. For example, these maps show the conditions for the tip of the crack to be closed and therefore no likelihood of fracture to exist. Finally, the strip yield model is used to investigate the elastic–plastic behaviour of the crack with increasing applied stress, for one size of the crack. The finite element method is used to provide comparisons with these results.

Fig. 1

a Residual stress components $\sigma _{rr}$ and $\sigma _{\theta \theta }$ versus r, b geometry of crack and residual stress

2 Residual stress field

The usual approach to generating a residual stress field is by modelling a process that introduces residual stress, such as elastic–plastic bending (Goudar and Smith 2013), welding (Smith and Smith 2009) or shrink-fitting (Mahmoudi et al. 2011). The generated residual stress field is usually complex and of fixed magnitude and distribution, making it difficult to form general conclusions about the influence of the residual stresses on subsequent behaviour. In this work we will generate a plane axisymmetric self-equilibrated residual stress distribution using the stress function (Timoshenko and Goodier 1982)

$$\begin{aligned} \varphi =\varphi \left( r \right) \end{aligned}$$

(1)

with

$$\begin{aligned} \sigma _{rr} =\frac{1}{r}\frac{\partial \varphi }{\partial r},\;\sigma _{\theta \theta } =\frac{\partial ^{2}\varphi }{\partial r^{2}} \end{aligned}$$

(2)

Using this approach, it is straightforward to vary the spacial extent of the residual stresses and their magnitude. We choose the stress function

$$\begin{aligned} \varphi =-\sigma _{\mathrm {RS}} R^{2}\exp \left[ {-\frac{r^{2}}{2R^{2}}} \right] \end{aligned}$$

(3)

giving

$$\begin{aligned} \sigma _{rr}= & {} \sigma _{\mathrm {RS}} \exp \left[ {-\frac{r^{2}}{2R^{2}}} \right] ,\;\nonumber \\ \sigma _{\theta \theta }= & {} \sigma _{\mathrm {RS}} \frac{R^{2}-r^{2}}{R^{2}}\exp \left[ {-\frac{r^{2}}{2R^{2}}} \right] \end{aligned}$$

(4)

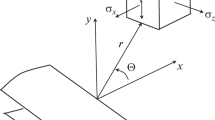
which for positive $\sigma _{\mathrm {RS}}$ produces a residual stress field consisting of a circle of tensile tangential stress $\sigma _{\theta \theta }$ of radius R centred at the origin surrounded by compressive tangential stress that decays to zero away from the origin. Figure 1a plots the stresses $\sigma _{rr}$ and $\sigma _{\theta \theta }$ versus r and Fig. 1b shows the geometry. The minimum value of $\sigma _{\theta \theta }$ is $-2\sigma _{RS} \hbox {e}^{-3/2}$ at $x=\sqrt{3}R$. When the residual stress field is introduced into an elastic–plastic material, the magnitude of $\sigma _{RS}$ must be less than the yield stress of the material to avoid plasticity.

The eigenstrain method is an alternative approach to the use of a stress function for the introduction of a residual stress in a finite element analysis, see for example Ribeiro and Hill (2016). “Appendix A” provides a calculation of the eigenstrain corresponding to the stress function of Eq. (3).

Although the residual stress produced by the stress function of Eq. (3) is of simple form, it matches closely residual stress fields produced by a variety of different methods. For example, Fig. 2a shows the centre hole drilling results of Formby and Griffiths (1977) for a 4 mm thick rectangular steel plate heated locally between two circular copper heaters with the geometry in Fig. 2b. The heating causes the steel to yield which leaves a tensile residual stress in the centre of the plate once it cools. The results of a series of residual stress measurements are shown in Fig. 3a for a 10 mm thick circular stainless steel disc that has been compressed between two circular tool steel indenters as shown in Fig. 3b (Pagliaro et al. 2009). In this case the residual stress in the centre of the plate is compressive. Finally, Fig. 4a shows contour and neutron diffraction measurements of residual stress in a butt-welded steel plate (Balakrishnan et al. 2018). Figure 4b shows the dimensions of the plate and Fig. 4c the detail of the weld. In all sets of experiments the dimensions of the plates were not large enough for the residual stress to decay to zero. Furthermore, the residual stress distributions in Figs. 2 and Fig. 4 will not be axisymmetric.

In the following sections the axisymmetric residual stress distribution of Eq. (4) is first transformed into the rectangular components defined in Fig. 1b (Timoshenko and Goodier 1982).

$$\begin{aligned} \sigma _{xx}= & {} \sigma _{\mathrm {RS}} \left[ {1-\frac{y^{2}}{R^{2}}} \right] \exp \left[ {-\frac{x^{2}}{2R^{2}}-\frac{y^{2}}{2R^{2}}} \right] \nonumber \\ \sigma _{yy}= & {} \sigma _{\mathrm {RS}} \left[ {1-\frac{x^{2}}{R^{2}}} \right] \exp \left[ {-\frac{x^{2}}{2R^{2}}-\frac{y^{2}}{2R^{2}}} \right] \nonumber \\ \sigma _{xy}= & {} \sigma _{\mathrm {RS}} \left[ {-\frac{xy}{R^{2}}} \right] \exp \left[ {-\frac{x^{2}}{2R^{2}}-\frac{y^{2}}{2R^{2}}} \right] \end{aligned}$$

(5)

Fig. 2

a Comparison of residual stress produced by the stress function with residual stress measured in a heated rectangular plate, b geometry of the heated plate (Formby and Griffiths 1977)

Fig. 3

a Comparison of residual stress produced by the stress function with residual stress measured in an indented circular plate, b geometry of the indented plate (Pagliaro et al. 2009)

Fig. 4

a Comparison of residual stress produced by the stress function with residual stress measured in a butt-welded steel plate, b geometry of the welded plate, c detail of weld (Balakrishnan et al. 2018)

The analytical work only requires the $\sigma _{yy}$ component of stress for $y=0$ to evaluate residual stress intensity factors. To simplify the resulting expressions, we write

$$\begin{aligned} \left. {\sigma _{yy} } \right| _{y=0} =\sigma _{\mathrm {RS}} f\left( x \right) \end{aligned}$$

(6)

where

$$\begin{aligned} f\left( x \right) =\left[ {1-\frac{x^{2}}{R^{2}}} \right] \exp \left[ {-\frac{x^{2}}{2R^{2}}} \right] \end{aligned}$$

The form of the stress $\sigma _{yy}$ at $y=0$ versus x is equivalent to that of $\sigma _{\theta \theta }$ versus r shown in Fig. 1a and is identical to that used by Terada (1976). Other stress functions could be used to generate a residual stress field and would give different detailed results to those presented here. Our aim however is to explore the effect of a simple residual stress field on the behaviour of a crack, although our simple residual stress field includes all the general attributes of a residual stress field.

Although the distribution of the residual stress has been determined, the method of its creation has not been defined. Therefore, the effect of the process that caused the residual stress on the subsequent material properties, the state of hardening for example, has not been included. In the work described here the material is taken to be elastic-perfectly plastic, but in general parameters defining the history of the material in addition to the residual stresses would have to be prescribed (Lei et al. 2000).

3 Elastic crack behaviour

In this section the elastic behaviour of a crack in a residual stress field is studied when subjected to additional tensile or compressive uniaxial applied stress. The geometry of the crack is shown in Fig. 1b. Depending on the length of the crack, the level of applied stress and the magnitude of the residual stresses the crack may be closed, partially open or fully open. These different crack states are defined in Fig. 5. A crack behaviour map may be used to describe the behaviour of the crack, where one axis represents the length of the crack and the other the level of the applied stress. Different states of opening of the crack occupy different regions of the crack behaviour map. We first present the crack behaviour map for positive $\sigma _{\mathrm {RS}}$, that is when the tangential residual stress is tensile at the centre. Throughout this paper we will refer to this case as tensile residual stress. We then describe the analysis that allows the boundaries between the regions of crack behaviour to be found. Finally, we present the crack behaviour map for negative $\sigma _{\mathrm {RS}}$, referred to here as the case of compressive residual stress.

Fig. 5

Full set of crack geometries for a crack located at the centre of the residual stress distribution of Fig. 1 combined with applied stress acting in the y direction

Fig. 6

Elastic crack behaviour map for tensile residual stress

3.1 Tensile residual stress

Figure 6 shows the behaviour of the crack for tensile residual stress and tensile and compressive applied stress. The half-length of the crack c is normalised with respect to the size of the tensile region of the residual stress field R and the applied stress $\sigma _{\mathrm {APP}}$ is normalised with respect to $\sigma _{\mathrm {RS}}$. As an example, the line segment AC in Fig. 6 forms the boundary between two regions of crack behaviour. Above the line, for higher magnitudes of applied stress, the crack is fully open. Below the line the crack is partially open: closed at the tip but open in the centre. These two crack states are defined in Fig. 5.

For all sizes of crack, the crack is always closed if the applied stress is compressive and greater in magnitude than the value of the residual stress at $x=0$, that is $\sigma _{\mathrm {APP}} <-\sigma _{\mathrm {RS}}$. As the magnitude of the compressive applied stress is reduced, the crack opens first at $x=0$ when the sum of the applied and residual stresses equals zero. The boundary between the fully closed and partially open regions of crack behaviour, the line AB, is therefore given by ${\sigma _{\mathrm {APP}} }/{\sigma _{\mathrm {RS}} }=-1$

Once the crack is partially open, progressively increasing the magnitude of the applied stress will eventually cause the crack to open completely. The magnitude of applied stress to open the crack fully depends on the length of the crack. For crack half-lengths less than $\sqrt{5}R$ ($c/R\approx 2.236)$ the boundary between the fully open and partially open regions is the line AC. This line is given by the condition that the total stress intensity factor $K_{\mathrm {TOT}}$ given by the sum of stress intensity factors due to the applied stress $K_{\mathrm {APP}}$ and the residual stress $K_{\mathrm {RS}}$ is equal to zero:

$$\begin{aligned} K_{\mathrm {TOT}} =K_{\mathrm {APP}} +K_{\mathrm {RS}} =0 \end{aligned}$$

(7)

where

$$\begin{aligned} K_{\mathrm {APP}}= & {} \sigma _{\mathrm {APP}} \sqrt{\pi c} \\ K_{\mathrm {RS}}= & {} \frac{2\sigma _{\mathrm {RS}} }{\sqrt{\pi c}}\mathop \int \limits _{x=0}^c {\frac{f\left( x \right) \hbox {d}x}{\sqrt{1-{x^{2}}/c^{2}}}} \end{aligned}$$

Note that $K_{\mathrm {APP}}$ depends on the applied stress and the length of the crack whereas for a given residual stress state, $K_{\mathrm {RS}}$ depends only on the length of the crack. $K_{\mathrm {RS}}$ is derived by integration of the expression for the stress intensity factor due to pairs of splitting forces applied to the crack surface (Tada et al. 2000).

For crack half-lengths greater than $\sqrt{5}R$, if the applied stress is high enough that the crack is fully open and the applied stress is then reduced the crack closes first at two points along the crack surface, symmetric about the centre of the crack. The position of these points depends on the crack length. The boundary between the fully open and partially open regions is the line CD. This line is given by the condition that the total opening displacement at the point of first contact $\delta _{\mathrm {TOT}}$ given by the sum of the displacement due to the applied stress $\delta _{\mathrm {APP}}$ and to the residual stress $\delta _{\mathrm {RS}}$ is equal to zero:

$$\begin{aligned} \delta _{\mathrm {TOT}} =\delta _{\mathrm {APP}} +\delta _{\mathrm {RS}} =0 \end{aligned}$$

(8)

where

$$\begin{aligned} \delta _{\mathrm {APP}}= & {} \frac{4\sigma _{\mathrm {APP}} \sqrt{c^{2}-d^{2}}}{{E}'} \\ \delta _{\mathrm {RS}}= & {} \frac{8\sigma _{\mathrm {RS}} }{\pi {E}'}\mathop \int \limits _{x=0}^d {f\left( x \right) \coth ^{-1}\sqrt{\frac{c^{2}-x^{2}}{c^{2}-d^{2}}}\hbox {d}x} \\&+\,\frac{8\sigma _{\mathrm {RS}} }{\pi {E}'}\mathop \int \limits _{x=d}^c {f\left( x \right) \tanh ^{-1}\sqrt{\frac{c^{2}-x^{2}}{c^{2}-d^{2}}}\hbox {d}x} \end{aligned}$$

${E}'$ is the effective modulus depending on whether plane stress or plane strain conditions apply

$$\begin{aligned} {E}'= & {} E\hbox { for plane stress} \\ {E}'= & {} \frac{E}{1-\nu ^{2}}\hbox { for plane strain} \end{aligned}$$

Again, $\delta _{\mathrm {RS}}$ is derived by integration of the expression for the crack opening due to pairs of splitting forces applied to the crack surface (Tada et al. 2000).

For crack half-lengths greater than $\sqrt{5}R$ a small regime of crack behaviour exists as shown in Fig. 5 where the crack is partially open: open at the tips and in the centre but closed between these points. This regime is bounded by the two lines CD and CE. To use closed form expressions to find the line CE requires a solution for the stress intensity factors at the multiple tips of three collinear cracks. We have not attempted to do this, instead the line CE in Fig. 4 has been found using finite element analysis.

In addition to the behaviour of the crack for different applied stresses, stress intensity factors may also be calculated. For example, Fig. 7 shows the total stress intensity for a crack of half-length $c=R$ versus the applied stress. This corresponds to the vertical dashed line in Fig. 6 where $c/R=1$. At the point marked X the crack begins to open at the centre but is closed at the tip. At the point marked Y, when ${\sigma _{\mathrm {APP}} }/{\sigma _{\mathrm {RS}} }\approx -0.4446$, the crack is open completely. The stress intensity factor is zero for points between X and Y. For points above Y the total stress intensity factor $K_{\mathrm {TOT}}$ is calculated by

$$\begin{aligned} K_{\mathrm {TOT}} =K_{\mathrm {APP}} +K_{\mathrm {RS}} \end{aligned}$$

(9)

where $K_{\mathrm {APP}}$ and $K_{\mathrm {RS}}$ are given by Eq. (7). Note that when $\sigma _{\mathrm {APP}} =0$, the point Z in Fig. 6, $K_{\mathrm {APP}} =0$ and $K_{\mathrm {TOT}} =K_{RS} \approx 0.4446\;\sigma _{\mathrm {RS}} \sqrt{\pi c}$. As shown in Fig. 7, once the crack opens at the tip, the total stress intensity varies linearly with the applied stress.

Fig. 7

Elastic normalised stress intensity factor $K/{\sigma _{RS} \sqrt{\pi c}}$ and normalised crack opening a / c versus normalised applied stress ${\sigma _{APP} }/{\sigma _{RS} }$ for tensile residual stress and a normalised crack length of $c/R=1$

The half-length of the open portion of the crack a (see Fig. 5 for the geometry of a partially open crack, closed at the tip and open at the centre) is calculated by the condition that the stress intensity factor at the point where the crack closes ($x=a)$ must be zero. Therefore a is calculated by

$$\begin{aligned} K_{\mathrm {TOT}} =K_{\mathrm {APP}} +K_{RS} =0 \end{aligned}$$

(10)

where $K_{\mathrm {APP}}$ and $K_{\mathrm {RS}}$ are given by the same expressions as in Eq. (7), except that c is replaced by a. Figure 7 also shows the half-length of the open portion of the crack a versus the applied stress. The crack begins to open at an applied stress of ${\sigma _{\mathrm {APP}} }/{\sigma _{\mathrm {RS}} }=-1$ and is open completely ($a/c=1)$ for applied stresses higher than ${\sigma _{\mathrm {APP}} }/{\sigma _{\mathrm {RS}} }\approx -0.4446$.

Fig. 8

Details of the finite element model used to calculate stress intensity factors

The finite element results shown in Fig. 7 for comparison were evaluated using the Abaqus 6.11 finite element system using a quarter mesh with symmetry constraints applied on the lower and left hand edges of the mesh as shown in Fig. 8. The residual stress distribution of Eq. (5) was prescribed using the SIGINI user subroutine facility in Abaqus. The width of the fine region of elements around the crack was four times the half-length of the crack and the width of the complete mesh 75 times the half-length of the crack. Plane stress conditions were used with linear quadrilateral elements CPS4. Calculations of stress intensity factors in this work used the JEDI code (Beardsmore 2008). This uses a contour integral evaluation and conveniently defines the contours automatically.

3.2 Compressive residual stress

The behaviour of the crack for negative $\sigma _{\mathrm {RS}}$, that is when the tangential residual stress is compressive at the centre, is shown in Fig. 9. The half-length of the crack c is normalised with respect to the size of the compressive region of the residual stress field R and the applied stress $\sigma _{\mathrm {APP}}$ is normalised with respect to $\left| {\sigma _{\mathrm {RS}} } \right|$.

Again, exact analytical solutions have been developed to define the boundaries between the regions of crack behaviour. However, for the case of compressive residual stress the calculations are generally more involved. For tensile residual stress, apart from a small region where the crack is open at the tips and the centre but closed in between, the analysis can use stress intensity factor solutions for a single crack. For compressive residual stress however, Fig. 9 shows a large region of behaviour where the crack is open at the tip but closed in between. For the analysis of this case, stress intensity factor solutions for twin collinear cracks are required.

Fig. 9

Elastic crack behaviour map for compressive residual stress

Reference to Fig. 9 shows that the crack is fully closed provided the applied load is less than a value that depends on the crack length. When the crack half-length is less than $c=\sqrt{3}R \left( {c/R<1.732} \right)$ the crack opens first at the tip. Points on the line AC in the figure are therefore given by the condition that the sum of the residual stress and the applied stress equals zero at the crack tip:

$$\begin{aligned} \sigma _{\mathrm {APP}} +\sigma _{\mathrm {RS}} f\left( c \right) =0 \end{aligned}$$

(11)

When the crack half-length is greater than $c=\sqrt{3}R$, the crack opens first at the point of maximum tensile residual stress which occurs at $x=\sqrt{3}R$. Therefore, the line CE is given by

$$\begin{aligned} \sigma _{\mathrm {APP}} +2\sigma _{RS} \hbox {e}^{-3/2}=0 \end{aligned}$$

(12)

For crack half-lengths greater than $c=\sqrt{3}R$, the crack becomes open at the tip when the stress intensity at the tip, $x=c$, is zero. The geometry of the crack is equivalent to twin symmetric collinear cracks and an analytical solution to find the boundaries between different regions of crack behaviour requires stress intensity factors solutions for twin cracks. Therefore, points on the line CD are given by simultaneous solution of the equations

$$\begin{aligned} K_{\mathrm {TOT}}^a= & {} K_{\mathrm {APP}}^a +K_{\mathrm {RS}}^a =0 \nonumber \\ K_{\mathrm {TOT}}^c= & {} K_{\mathrm {APP}}^c +K_{\mathrm {RS}}^c =0 \end{aligned}$$

(13)

$K_{\mathrm {APP}}^a$ and $K_{\mathrm {APP}}^c$ are the stress intensity factors for twin cracks with crack tips located at $x=\pm \, a$ and $x=\pm \,c$ due to a uniform applied stress. $K_{\mathrm {RS}}^a$ and $K_{\mathrm {RS}}^c$ are the corresponding stress intensity factors for residual stress. Equation (13) first requires the stress intensity factor at the inner tip of the twin cracks at $x=\pm \,a$ to be zero. This provides the condition that twin cracks represent a single crack, closed between $x=a$ and $x=-a$. Equation (13) also requires the stress intensity factor at the outer tips, at $x=\pm \,c$, to be zero. This provides the condition that the crack is just open at the tips. Solution of Eq. (13) provides values for a and $\sigma _{\mathrm {APP}}$ for prescribed values for c and $\sigma _{\mathrm {RS}}$. The stress intensity factors in Eq. (13) are calculated using the expressions in “Appendix B” and are given by

$$\begin{aligned} K_{\mathrm {APP}}^a= & {} \sigma _{\mathrm {APP}} \sqrt{\pi a}\frac{1}{a\sqrt{c^{2}-a^{2}}}\left\{ {c^{2}\frac{E\left( m \right) }{K\left( m \right) }-a^{2}} \right\} \\ K_{\mathrm {APP}}^c= & {} \sigma _{\mathrm {APP}} \sqrt{\pi c} \frac{c}{\sqrt{c^{2}-a^{2}}} \left\{ {1-\frac{E\left( m \right) }{K\left( m \right) }} \right\} \\ K_{\mathrm {RS}}^a= & {} \frac{2\sigma _{\mathrm {RS}} }{\sqrt{\pi a}\sqrt{c^{2}-a^{2}}}\mathop \int \limits _{x=a}^c f\left( x \right) \left\{ \frac{x\sqrt{c^{2}-x^{2}}}{\sqrt{x^{2}-a^{2}}}\right. \\&\left. +\,c\left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} dx \\ K_{\mathrm {RS}}^c= & {} \frac{2\sigma _{\mathrm {RS}} }{\sqrt{\pi c}\sqrt{c^{2}-a^{2}}}\mathop \int \limits _{x=a}^c f\left( x \right) \left\{ \frac{x\sqrt{x^{2}-a^{2}}}{\sqrt{c^{2}-x^{2}}}\right. \\&\left. -\,c\left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} dx \end{aligned}$$

where

$$\begin{aligned} m=1-\frac{a^{2}}{c^{2}}, \quad \phi =\sin ^{-1}\sqrt{\frac{c^{2}-x^{2}}{c^{2}-a^{2}}} \end{aligned}$$

$K\left( m \right) , E\left( m \right) , F\left( {\phi ,m} \right)$ and $E\left( {\phi ,m} \right)$ are complete and incomplete elliptic integrals of the first and second kinds.

For all sizes of crack, the crack is always fully open provided the applied stress is high enough. If the crack is fully open and the applied stress is then reduced the crack closes first at the centre. The applied stress at which closure occurs depends on the length of the crack. The boundary between the fully open and partially open regions is the line AB. This line is given by the condition that the total opening displacement $\delta _{\mathrm {TOT}}$ at the centre of the crack due to the applied stress $\delta _{\mathrm {APP}}$ and the residual stress $\delta _{\mathrm {RS}}$ is equal to zero:

$$\begin{aligned} \delta _{\mathrm {TOT}} =\delta _{\mathrm {APP}} +\delta _{\mathrm {RS}} =0 \end{aligned}$$

(14)

where (Tada et al. 2000)

$$\begin{aligned} \delta _{\mathrm {APP}}= & {} \frac{4\sigma _{\mathrm {APP}} c}{{E}'} \\ \delta _{\mathrm {RS}}= & {} \frac{8\sigma _{\mathrm {RS}} }{\pi {E}'}\mathop \int \limits _{x=0}^c {f\left( x \right) \cosh ^{-1}\frac{c}{x}\hbox {d}x} \end{aligned}$$

Fig. 10

Elastic normalised stress intensity factor $K/{\sigma _{RS} \sqrt{\pi c}}$ and normalised crack opening a / c versus normalised applied stress ${\sigma _{APP} }/{\sigma _{RS} }$ for compressive residual stress and a normalised crack length of $c/R=1$

In the same way as for tensile residual stress, stress intensity factors may be calculated for cracks in a compressive residual stress field with superimposed applied stress. For example, Fig. 10 shows the stress intensity factor normalised by $\sigma _{\mathrm {RS}} \sqrt{\pi c}$ for a crack of half-length $c=R$, versus the applied stress. This corresponds to the vertical dashed line in Fig. 9 with $c/R=1$. At the point marked X in Fig. 9 the crack begins to open at the tip but is closed at the centre. At the point marked Y the crack is open completely. The applied stress corresponding to point Y is calculated to be given by ${\sigma _{\mathrm {APP}} }/{\left| {\sigma _{\mathrm {RS}} } \right| }\approx 0.7910$. The procedure for calculating the stress intensity factor for points between X and Y is first to choose a value for the partially open half-length a (see Fig. 5 for the geometry of a partially open crack, open at the tip and closed at the centre) where $0<a<c$. The applied stress corresponding to the chosen value of a is determined from the condition that the stress intensity factor at a is zero:

$$\begin{aligned} K_{\mathrm {TOT}}^a =K_{\mathrm {APP}}^a +K_{\mathrm {RS}}^a =0 \end{aligned}$$

(15)

Once the applied stress corresponding to the chosen value of a is determined, the stress intensity factor $K_{\mathrm {TOT}}^c$ at the tip of the crack is calculated by

$$\begin{aligned} K_{\mathrm {TOT}}^c =K_{\mathrm {APP}}^c +K_{\mathrm {RS}}^c \end{aligned}$$

(16)

For points above Y in Fig. 9 the crack is open completely and the stress intensity factor is

$$\begin{aligned} K_{\mathrm {TOT}} =K_{\mathrm {APP}} +K_{RS} \end{aligned}$$

(17)

where $K_{\mathrm {APP}}$ and $K_{\mathrm {RS}}$ are defined in Eq. (7).

Figure 10 also shows the half-length of the open portion of the crack a normalised by c for a crack of half-length $c=R$ versus the applied stress. At the point marked X in Fig. 9 the crack begins to open at the tip and $a=c$. At the point marked Y the crack just opens fully and $a=0$. The applied stress corresponding to each value of a has already been found during the calculation of the stress intensity factor.

4 Strip yield model

We will now use the strip yield model of Dugdale (1960) and Barrenblatt (1962) to examine the effect of small-scale yielding on the behaviour of a crack in a residual stress field. We will not present revised crack behaviour maps valid for small-scale yielding since in general these maps are similar to the maps for elastic behaviour of Figs. 6 and 9. Instead we choose one crack length defined by $c=R$ and study the behaviour of the crack as the applied load is increased from an initial state where the crack is fully closed. The approach described in this section can be used for other crack lengths.

Strip yield models have been used before in the context of residual stress. For example, Becker (1997) and Radayev and Stepanova (2001) examined residual stresses caused by a stress cycle applied to a crack while Liu (1998) calculated plastic zone sizes and crack opening displacements for cracks within a residual stress distribution caused by welding. In addition, Wang (1999) used a strip yield model for a crack in a residual stress field to analyse the effect of the residual stresses on crack closure and hence their influence on fatigue crack growth rates. We remark that the strip yield model has also been used by Chell (1976) for example to consider other crack geometries, Kfouri (1979) to look at biaxial loading, Daniewicz (1994) to include the effects of strain hardening and Neimitz (2004) for cases where in-plane and out-of-plane constraint exist.

Fig. 11

Geometry of the strip yield model for a single crack

4.1 Tensile residual stress

For tensile residual stress we consider an initial state where the applied stress is sufficient to ensure the crack is fully closed. For a crack of half-length $c=R$ the applied stress $\sigma _{\mathrm {APP}}$ must be less than (more compressive than) $-\sigma _{\mathrm {RS}}$. As the applied stress is increased the crack opens first in the centre, as described in the previous section. It is only when the crack has opened fully to the tip that the small-scale yielding behaviour is different to the elastic behaviour. When the applied stress is larger than that to open the crack fully the strip yield model may be used to calculate the effective stress intensity factor.

Figure 11 shows the geometry of the crack when fully open. A yielded zone of length $\rho$ forms ahead of the crack tip. The size of this yielded zone is calculated using the condition that the total stress intensity factor for an extended crack of half-length $c+\rho$ is zero. When residual stresses act in addition to the applied stress, the total stress intensity factor $K_{\mathrm {TOT}}$ is calculated as the sum of the stress intensity factors due to the applied stress $K_{\mathrm {APP}}$, the residual stress $K_{\mathrm {RS}}$ and stresses applied to the crack tip to represent the yield zone $K_{\mathrm{Y}}$. Therefore

$$\begin{aligned} K_{\mathrm {TOT}} =K_{\mathrm {APP}} +K_{\mathrm {RS}} +K_{\mathrm{Y}} =0 \end{aligned}$$

(18)

where (Tada et al. 2000)

$$\begin{aligned} K_{\mathrm {APP}}= & {} \sigma _{\mathrm {APP}} \sqrt{\pi \left( {c+\rho } \right) } \\ K_{\mathrm {RS}}= & {} \frac{2\sigma _{\mathrm {RS}} }{\sqrt{\pi \left( {c+\rho } \right) }}\mathop \int \limits _{x=0}^{c+\rho } {\frac{f\left( x \right) dx}{\sqrt{1-{x^{2}}/{\left( {c+\rho } \right) ^{2}}}}} \\ K_{\mathrm{Y}}= & {} 2\sigma _{\mathrm{Y}} \sqrt{\frac{c+\rho }{\pi }}\sin ^{-1}\frac{c}{c+\rho }-\sigma _{\mathrm{Y}} \sqrt{\pi \left( {c+\rho } \right) } \\ \end{aligned}$$

Solution of Eq. (18) gives the size of the plastic zone $\rho$. The effective stress intensity factor will be evaluated using the technique of Burdekin and Stone (1966), which requires the crack opening displacement to be calculated at $x=c$. The total crack opening displacement $\delta _{\mathrm {TOT}}$ is evaluated as the sum of the crack opening due to the applied stress $\delta _{\mathrm {APP}}$, the residual stress $\delta _{\mathrm {RS}}$ and the stresses in the yielded zone $\delta _{\mathrm{Y}}$. That is

$$\begin{aligned} \delta _{\mathrm {TOT}} =\delta _{\mathrm {APP}} +\delta _{\mathrm {RS}} +\delta _{\mathrm{Y}} \end{aligned}$$

(19)

where (Tada et al. 2000)

$$\begin{aligned} \delta _{\mathrm {APP}}= & {} \frac{4\sigma _{\mathrm {APP}} }{{E}'}\sqrt{\left( {c+\rho } \right) ^{2}-c^{2}} \\ \delta _{\mathrm {RS}}= & {} \frac{8\sigma _{\mathrm {RS}} }{\pi {E}'}\mathop \int \limits _{x=0}^c {f\left( x \right) } \coth ^{-1}\sqrt{\frac{\left( {c+\rho } \right) ^{2}-x^{2}}{\left( {c+\rho } \right) ^{2}-c^{2}}}dx \\&+\,\frac{8\sigma _{\mathrm {RS}} }{\pi {E}'}\mathop \int \limits _{x=c}^{c+\rho } {f\left( x \right) } \tanh ^{-1}\sqrt{\frac{\left( {c+\rho } \right) ^{2}-x^{2}}{\left( {c+\rho } \right) ^{2}-c^{2}}}dx \\ \delta _{\mathrm{Y}}= & {} -\frac{4\sigma _{\mathrm{Y}} }{{E}'}\sqrt{\left( {c+\rho } \right) ^{2}-c^{2}} \\&+\,\frac{8\sigma _{\mathrm{Y}} }{\pi {E}'}\left[ \sin ^{-1}\left( {\frac{c}{c+\rho }} \right) \sqrt{\left( {c+\rho } \right) ^{2}-c^{2}}\right. \\&\left. +\,c\ln \left( {\frac{c+\rho }{c}} \right) \right] \end{aligned}$$

Finally, the effective stress intensity factor is obtained by

$$\begin{aligned} K_{\mathrm {EFF}} =\sqrt{{E}'\sigma _{\mathrm{Y}} \delta _{\mathrm {TOT}} } \end{aligned}$$

(20)

Figure 12 shows normalised effective stress intensity factors versus normalised applied stress for four different values for the yield stress given by ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {RS}} }=1,\;1.5,\;2,\;2.5$. Note that we have chosen to define the relative magnitude of the yield stress and residual stress by ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {RS}} }$ rather than ${\sigma _{\mathrm {RS}} }/{\sigma _{\mathrm{Y}} }$ so that ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {RS}} }$ is asymptotic to ${\sigma _{\mathrm {APP}} }/{\sigma _{\mathrm {RS}} }$. For example, when ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {RS}} }=2$, $\sigma _{\mathrm {RS}} ={\sigma _{\mathrm{Y}} }/2$ and the curve is asymptotic to ${\sigma _{\mathrm {APP}} }/{\sigma _{\mathrm {RS}} }=2$ which is equivalent to ${\sigma _{\mathrm {APP}} }/{\sigma _{\mathrm{Y}} }=1$. Lower values of ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {RS}} }$ represent higher magnitudes of residual stress. The figure also shows two-dimensional plane stress finite element results obtained for $K_{\mathrm {EFF}}$ using the calculation

$$\begin{aligned} K_{\mathrm {EFF}} =\sqrt{{E}'J} \end{aligned}$$

(21)

where J is the value of the J-integral evaluated using the JEDI procedure (Beardsmore 2008). Very good agreement is obtained, even for applied stresses approaching the yield stress where large plastic zones develop and small-scale yielding conditions certainly do not exist.

Fig. 12

Elastic–plastic normalised effective stress intensity factor ${K_{\mathrm {EFF}} }/{\sigma _{\mathrm {RS}} \sqrt{\pi c}}$ versus normalised applied stress ${\sigma _{APP} }/{\sigma _{RS} }$ for tensile residual stress and a normalised crack length of $c/R=1$

4.2 Compressive residual stress

Again, we consider an initial state where the applied stress is sufficient to ensure the crack is fully closed. For a crack of half-length $c=R$ the applied stress $\sigma _{\mathrm {APP}}$ must be less than zero. For the case of a compressive residual stress the crack opens first at the tips and therefore the small-scale yielding behaviour will be different to the elastic behaviour. The strip yield model may still be used to calculate the effective stress intensity factor but complicated by the need to use a twin crack geometry. When the applied stress is high enough to open the crack completely, the same strip yield model as for tensile residual stress case can be used.

A strip yield model combined with a twin collinear crack geometry has been used previously, most often in the context of multiple site damage, where adjacent fatigue cracks interact with each other. Examples of such work are: Smith (1964), Theocaris (1983), Collins and Cartwright (2001), Nishimura (2002), Xu et al. (2011), Bhargava and Hasan (2011), Chang and Kotousov (2012) and Chen (2014).

Fig. 13

Geometry of the strip yield model for twin cracks

Figure 13 shows the geometry of the crack when partially open. A yielded zone of length $\rho$ forms ahead of the crack tip which is again calculated using the condition that the total stress intensity factor for the extended crack must be zero. However, there is an additional requirement that the total stress intensity factor at the inner crack tip where $x=a$ must also be zero, although there is no plastic zone at the inner tip. For this case then

$$\begin{aligned} K_{\mathrm {TOT}}^a= & {} K_{\mathrm {APP}}^a +K_{\mathrm {RS}}^a +K_{\mathrm{Y}}^a =0 \nonumber \\ K_{\mathrm {TOT}}^{c+\rho }= & {} K_{\mathrm {APP}}^{c+\rho } +K_{\mathrm {RS}}^{c+\rho } +K_{\mathrm{Y}}^{c+\rho } =0 \end{aligned}$$

(22)

where

$$\begin{aligned} K_{\mathrm {APP}}^a= & {} \sigma _{\mathrm {APP}} \sqrt{\pi a}\frac{1}{a\sqrt{\left( {c+\rho } \right) ^{2}-a^{2}}}\\&\times \left\{ {\left( {c+\rho } \right) ^{2}\frac{E\left( m \right) }{K\left( m \right) }-a^{2}} \right\} \\ K_{\mathrm {APP}}^{c+\rho }= & {} \sigma _{\mathrm {APP}} \sqrt{\pi \left( {c+\rho } \right) } \frac{c+\rho }{\sqrt{\left( {c+\rho } \right) ^{2}-a^{2}}}\\&\times \left\{ {1-\frac{E\left( m \right) }{K\left( m \right) }} \right\} \\ K_{\mathrm {RS}}^a= & {} \frac{2\sigma _{\mathrm {RS}} }{\sqrt{\pi a}\sqrt{\left( {c+\rho } \right) ^{2}-a^{2}}}\mathop \int \limits _{x=a}^{c+\rho } f\left( x \right) \\&\times \left\{ \frac{x\sqrt{\left( {c+\rho } \right) ^{2}-x^{2}}}{\sqrt{x^{2}-a^{2}}}+\left( {c+\rho } \right) \right. \\&\left. \left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} dx \\ K_{\mathrm {RS}}^{c+\rho }= & {} \frac{2\sigma _{\mathrm {RS}} }{\sqrt{\pi \left( {c+\rho } \right) }\sqrt{\left( {c+\rho } \right) ^{2}-a^{2}}}\mathop \int \limits _{x=a}^{c+\rho } f\left( x \right) \\&\times \left\{ \frac{x\sqrt{x^{2}-a^{2}}}{\sqrt{\left( {c+\rho } \right) ^{2}-x^{2}}}-\left( {c+\rho } \right) \right. \\&\left. \left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} dx \\ K_{\mathrm{Y}}^a= & {} \frac{-2\sigma _{\mathrm{Y}} }{\sqrt{\pi a}\sqrt{\left( {c+\rho } \right) ^{2}-a^{2}}}\mathop \int \limits _{x=c}^{c+\rho }\\&\times \left\{ \frac{x\sqrt{\left( {c+\rho } \right) ^{2}-x^{2}}}{\sqrt{x^{2}-a^{2}}}+\left( {c+\rho } \right) \right. \\&\left. \left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} dx \\ K_{\mathrm{Y}}^{c+\rho }= & {} \frac{-2\sigma _{\mathrm{Y}} }{\sqrt{\pi \left( {c+\rho } \right) }\sqrt{\left( {c+\rho } \right) ^{2}-a^{2}}}\mathop \int \limits _{x=c}^{c+\rho } \\&\times \left\{ \frac{x\sqrt{x^{2}-a^{2}}}{\sqrt{\left( {c+\rho } \right) ^{2}-x^{2}}}-\left( {c+\rho } \right) \right. \\&\left. \left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} dx \end{aligned}$$

and

$$\begin{aligned} m=1-\frac{a^{2}}{\left( {c+\rho } \right) ^{2}}, \quad \phi =\sin ^{-1}\sqrt{\frac{\left( {c+\rho } \right) ^{2}-x^{2}}{\left( {c+\rho } \right) ^{2}-a^{2}}} \end{aligned}$$

The stress intensity factors in Eq. (22) are calculated using the expressions in “Appendix B”. Note that $K_{\mathrm{Y}}^a$ is the contribution of the yielded zone at the outer crack tip to the stress intensity factor at the inner crack tip.

Solution of Eq. (22) gives the size of the plastic zone $\rho$ and the position of the inner crack tip a. Again, evaluation of the effective stress intensity factor requires the crack opening displacement to be calculated at $x=c$. The total crack opening displacement $\delta _{\mathrm {TOT}}$ is evaluated as the sum of the crack opening due to the applied stress $\delta _{\mathrm {APP}}$, the residual stress $\delta _{\mathrm {RS}}$ and the stresses in the yielded zone $\delta _{\mathrm{Y}}$. That is

$$\begin{aligned} \delta _{\mathrm {TOT}} =\delta _{\mathrm {APP}} +\delta _{\mathrm {RS}} +\delta _{\mathrm{Y}} \end{aligned}$$

(23)

where (Tranter 1961)

$$\begin{aligned} \delta _{\mathrm {APP}} =\frac{4\left( {c+\rho } \right) \sigma _{\mathrm {APP}} }{{E}'}\left[ {E\left( {\phi ,m} \right) -\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }} \right] \end{aligned}$$

The crack opening displacements $\delta _{\mathrm {RS}}$ and $\delta _{\mathrm{Y}}$ are calculated using the method described in “Appendix B”. For pairs of unit point forces applied to the crack at $x=\pm \,d$ where $a<d<c$ we calculate the opening at $x=c$ using Eq. (35) to be

$$\begin{aligned} \delta _L \left( d \right) =\frac{2}{{E}'}\mathop \int \limits _{x=c}^{c+\rho } {K_x^c K_x^d dx} \end{aligned}$$

where $K_x^c$ is given by Eq. (33), with b replaced by c, and $K_x^d$ is given by Eq. (34). Similarly, for pairs of unit point forces applied to the crack at $x=\pm \,d$ where $c<d<c+\rho$ we calculate the opening at $x=c$ to be

$$\begin{aligned} \delta _R \left( d \right) =\frac{2}{{E}'}\mathop \int \limits _{x=d}^{c+\rho } {K_x^c K_x^d dx} \end{aligned}$$

Finally, $\delta _{\mathrm {RS}}$ and $\delta _{\mathrm{Y}}$ are calculated by

$$\begin{aligned} \delta _{\mathrm {RS}}= & {} \sigma _{\mathrm {RS}} \left[ \mathop \int \limits _{x=a}^c \delta _L \left( x \right) f\left( x \right) dx +\mathop \int \limits _{x=c}^{c+\rho } {\delta _R \left( x \right) f\left( x \right) dx} \right] \\ \delta _{\mathrm{Y}}= & {} -\sigma _{\mathrm{Y}} \mathop \int \limits _{x=c}^{c+\rho } {\delta _R \left( x \right) dx} \end{aligned}$$

The applied stress required to open the crack fully for small-scale yielding can be found using the same general procedure as for the linear elastic case: find the applied load for the central opening to be zero. We solve

$$\begin{aligned} \delta _{\mathrm {APP}} +\delta _{\mathrm {RS}} +\delta _{\mathrm{Y}} =0 \end{aligned}$$

(24)

where

$$\begin{aligned} \delta _{\mathrm {APP}}= & {} \frac{4\sigma _{\mathrm {APP}} \left( {c+\rho } \right) }{{E}'} \\ \delta _{\mathrm {RS}}= & {} \frac{8\sigma _{\mathrm {RS}} }{\pi {E}'}\mathop \int \limits _{x=0}^{c+\rho } {f\left( x \right) \cosh ^{-1}\frac{c+\rho }{x}\hbox {d}x} \\ \delta _{\mathrm{Y}}= & {} -\frac{8\sigma _{\mathrm{Y}} }{\pi {E}'}\mathop \int \limits _{x=c}^{c+\rho } {\cosh ^{-1}\frac{c+\rho }{x}\hbox {d}x} \end{aligned}$$

Figure 14 shows normalised effective stress intensity factors versus normalised applied stress for four different values for the yield stress given by ${\sigma _{\mathrm{Y}} }/{\left| {\sigma _{\mathrm {RS}} } \right| }=1,\;1.5,\;2,\;2.5$. The figure also shows finite element results obtained using the same procedure as for tensile residual stress.

Fig. 14

Elastic–plastic normalised effective stress intensity factor ${K_{\mathrm {EFF}} }/{\sigma _{\mathrm {RS}} \sqrt{\pi c}}$ versus normalised applied stress ${\sigma _{APP} }/{\sigma _{RS} }$ for compressive residual stress and a normalised crack length of $c/R=1$

Finally, Fig. 15 compares the results of the strip yield model for tensile residual stress and compressive residual stress, where the magnitude of the residual stress is equal to the yield stress, that is ${\sigma _{\mathrm{Y}} }/{\left| {\sigma _{\mathrm {RS}} } \right| }=1$. Figure 15 also shows the results for the standard strip yield model, the case with no residual stress. Finite element results are also shown. The kink in the strip yield model results for compressive residual stress at ${\sigma _{\mathrm {APP}} }/{\left| {\sigma _{\mathrm {RS}} } \right| }\approx 0.6957$ corresponds to the point when the crack becomes fully open. This compares with the corresponding point for linear elastic behaviour which occurs at ${\sigma _{\mathrm {APP}} }/{\left| {\sigma _{\mathrm {RS}} } \right| }\approx 0.7910$. Therefore, the effect of plasticity on the crack behaviour map for compressive residual stress of Fig. 9 is to lower the line AB slightly.

Fig. 15

Comparison of elastic–plastic normalised effective stress intensity factor ${K_{\mathrm {EFF}} }/{\sigma _{\mathrm{Y}} \sqrt{\pi c}}$ versus normalised applied stress ${\sigma _{\mathrm {APP}} }/{\sigma _{\mathrm{Y}} }$ with no residual stress, for tensile residual stress and for compressive residual stress with a normalised crack length of $c/R=1$

5 Discussion

5.1 Effect of residual stress on crack behaviour

Results have been obtained for a residual stress field derived from a closed form expression which allows the magnitude and extent of the field to be varied. Alternatively, the residual stresses may be obtained from a finite element simulation of a process that creates residual stress, welding for example, or indeed from a set of experimental measurements. The techniques described in this paper can then be used to provide exact values for the stress intensity factor for elastic material behaviour or approximate values for elastic–plastic behaviour. Although the detail of the crack behaviour will depend on the precise form of the residual stress distribution, general statements can be made of the crack behaviour based on the results presented here.

For a tensile residual stress field and with no superimposed applied stress, reference to the line ACE in Fig. 6 shows that the crack is open at the tip and therefore the stress intensity factor is greater than zero for almost all crack lengths, although the magnitude varies with the length of the crack. In Fig. 7 it can be seen that for elastic behaviour and for a crack of half-length $c=R$, once the crack is open the stress intensity factor increases linearly with applied stress. For elastic–plastic behaviour, Fig. 12 shows that the effective stress intensity factor is greater than the elastic value as the applied stress approaches the yield stress.

For a compressive residual stress field, reference to the line ACD in Fig. 9 shows that with no superimposed applied stress the crack is closed for crack lengths less that the size of the residual stress field and open at the tips for cracks greater than the size of the field. For elastic behaviour, Fig. 10 indicates that for a crack of half-length $c=R$, partial opening of the crack causes a nonlinear variation of stress intensity factor with applied stress until the crack opens completely whereupon the variation becomes linear. Again, it can be seen in Fig. 14 that elastic–plastic behaviour causes the effective stress intensity factors to be higher than the elastic value as the applied stress increases, but in comparison to the case of tensile residual stress the transition occurs at lower values of applied stress.

For both tensile and compressive residual stress, when the crack is partially open, open at the tips but closed elsewhere, the stress intensity factor is higher than would be calculated if crack closure was neglected.

This work has only considered cracks that are located symmetrically within a symmetric residual stress field. The case of an asymmetric crack, while more difficult to analyse, is certainly possible using the same techniques as have been developed here.

Table 1 Comparison of strip yield (SY) and finite element (FE) normalised effective stress intensity factors ${K_{\mathrm {EFF}} }/{\sigma _{\mathrm {APP}} \sqrt{\pi R}}$ for plane stress and plane strain with a yield stress ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {APP}} =1.5}$ for no residual stress, tensile residual stress of magnitude ${\sigma _{\mathrm {RS}} }/{\sigma _{\mathrm {APP}} }=1$ and compressive residual stress of magnitude ${\left| {\sigma _{\mathrm {RS}} } \right| }/{\sigma _{\mathrm {APP}} }=1$

Our results can be used to provide a first estimate of the likelihood of fracture for a crack in a residual stress field. They also enable the stress intensity factor range to be calculated from a given cycle of applied stress to allow predictions of fatigue crack growth to be made.

5.2 Influence of plane conditions

The results of the analysis of the elastic behaviour of the crack do not depend on plane conditions, that is identical results are obtained for plane strain as for plane stress. Although crack opening displacements are calculated using the effective modulus ${E}'$ which has a different value for plane strain compared to plane stress, these displacements are only used to find the boundary between different regions of crack behaviour. The positions of these boundaries are unaffected by the value of the effective modulus.

The strip yield model used previously does however assume plane stress conditions. The size of the strip yield zone calculated in the model depends only on the stress normal to the crack. If plane strain conditions exist, stresses would be developed perpendicular to the plane and these would influence the calculation of the strip yield zone. Although, Neimitz (2004) has described modifications to the strip yield model to account for variations of in-plane and out-of-plane constraint, no attempt has been made here to extend the analysis to plane strain. Rice (1974) remarked the effect of constraint on the size of the plastic zone was much more marked than the effect on the effective stress intensity factor. Nevertheless, a finite element study has been carried out to explore the sensitivity of the results to plane conditions.

Table 1 shows the results of the strip yield model and the finite element study for the case of no residual stress, tensile residual stress and compressive residual stress. Values of the normalised effective stress intensity factor are given for three different crack sizes $c/R=0.6,\;1.0,\;1.6$ and one magnitude of the yield stress relative to the applied stress defined by ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {APP}} =}1.5$.

For the case of no residual stress, effective stress intensities are higher for longer cracks but changing the plane condition does not have a significant effect, although the plane stress values are slightly higher than plane strain. For the range of conditions considered in the table, the strip yield results are within 3% of the finite element results for plane stress. For the case of tensile residual stress, the magnitude of the residual stress field is defined by ${\sigma _{\mathrm {RS}} }/{\sigma _{\mathrm {APP}} }=1$. Again, plane conditions do not have a significant effect and the agreement between the strip yield and finite element results is very good.

Finally, for the case of compressive residual stress the magnitude of the residual stress field is defined by ${\sigma _{\mathrm {RS}} }/{\sigma _{\mathrm {APP}} }=-1$. In contrast to the two previous sets of results, the plane stress condition gives effective stress intensity factors much lower than the plane strain condition when the crack length is smaller than the size of the residual stress field. This result can be understood by comparing the sizes of the plastic zones for the two plane conditions. Figure 16a shows the plastic zone sizes for the case of no residual stress for a crack size given by $c/R=1.0$ and a yield stress ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {APP}} =1.5}$. Both plastic zones are situated at the crack tip. The plane stress case gives a larger plastic zone. Figure 16b now shows the plastic zone sizes for the case of compressive residual stress for a smaller crack size given by $c/R=0.6$ and a yield stress ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {APP}} =1.5}$. For the plane stress condition, a yielded region exists away from the crack tip situated at the position of maximum tensile residual stress. This yielded region does not occur for plane strain conditions due to the additional constraint. The effective stress intensity factor and the crack tip plastic zone size for plane stress are much smaller than for plane strain. It is remarkable that the strip yield model gives very similar results to the plane stress finite element model, even though the strip yield model only accounts explicitly for a yielded region situated at the crack tip.

Fig. 16

Comparison of plastic zone sizes for plane stress and plane strain conditions with a yield stress ${\sigma _{\mathrm{Y}} }/{\sigma _{\mathrm {APP}} =1.5}$: a$c/{R=1.0}$ with no residual stress and b$c/{R=0.6}$ for compressive residual stress of magnitude ${\left| {\sigma _{\mathrm {RS}} } \right| }/{\sigma _{\mathrm {APP}} }=1$

5.3 Effect of crack length

The equations presented in Sections 3 and 4 of this paper may be used to find the stress intensity factors for cracks of different lengths, as presented in Fig. 17. The figure shows normalised stress intensity factor versus normalised crack length for elastic material behaviour for cases of no residual stress, and tensile and compressive residual stress with $\left| {\sigma _{\mathrm {RS}} } \right| =\sigma _{\mathrm {APP}}$. Figure 17 also shows normalised effective stress intensity factors for elastic–plastic behaviour where $\sigma _{\mathrm{Y}} =1.5\;\sigma _{\mathrm {APP}}$. These elastic–plastic results strictly are only valid for a static crack, that is where the crack has been introduced into a residual stress field all in one go. Sherry et al. (2006) suggest that the effective stress intensity factor for a crack that has been introduced progressively into a residual stress field is less than that for a static crack of the same length. In the figure, symbols are used to differentiate between LEFM and strip-yield results and do not represent FE calculated values.

Using Fig. 17, the stress intensity factor for a crack of a certain length can be compared with the fracture toughness of the material to determine the likelihood of fracture. When the fracture toughness of the material is low enough so that fracture occurs when the normalised stress intensity factor is of the order of 1 for example, as marked on the figure by a dashed line, it is essential that residual stresses are included in the assessment. For such conditions the crack size at fracture for tensile residual stress is much smaller than for the case of no residual stress, or of compressive residual stress. Conversely when the fracture toughness is higher so that fracture occurs when the normalised stress intensity factor is of the order of 2 for example, also marked on the figure by a dashed line, the fracture assessment is largely insensitive to the existence of residual stress.

Fig. 17

Normalised effective stress intensity factor versus normalised crack length for elastic behaviour (open symbols) and elastic–plastic behaviour with $\sigma _{\mathrm{Y}} =1.5\sigma _{\mathrm {APP}}$ (closed symbols)

5.4 Comparison with structural integrity procedures

Structural integrity codes such as R6 (EDF 2001) and BS 7910 (BSI 2013) introduce a V factor to account for the interaction between the applied and residual stresses due to plasticity. The V factor allows the fracture ratio, $K_r$ to be calculated which is used in the subsequent assessment of structural integrity:

$$\begin{aligned} K_r =\frac{K_{\mathrm {APP}} +VK_{\mathrm {RS}} }{K_{\mathrm {mat}} } \end{aligned}$$

(25)

where $K_{\mathrm {APP}}$ is the stress intensity factor calculated using an elastic analysis for applied stress, $K_{\mathrm {RS}}$ the stress intensity factor using an elastic analysis for residual stress and $K_{\mathrm {mat}}$ is the material toughness. A V factor closer to zero in Eq. (25) results in the calculation of a smaller fracture ratio and suggests a safer loading condition. Recommended procedures to determine V factors can be found in R6 or BS 7910. Both codes suggest that V should be taken to be zero if the residual stress is compressive, although this can be seen to be overly conservative by reference to Fig. 17 (at $c/R=0.5$, the stress intensity factor for combined applied and compressive residual stress is much less than that for applied stress only).

The analytical methods presented in this paper allow the V factor to be estimated without detailed finite element analysis using the equation

$$\begin{aligned} V=\frac{K_{\mathrm {APP}} }{K_{\mathrm {RS}} }\left( {\frac{K_{\mathrm {EFF}} }{K_{\mathrm {EFF}}^{\mathrm {APP}} }-1} \right) \end{aligned}$$

(26)

where $K_{\mathrm {EFF}}$ is the effective stress intensity factor calculated using an elastic–plastic analysis for combined applied load and residual stress and $K_{\mathrm {EFF}}^{\mathrm {APP}}$ is the effective stress intensity factor for an elastic–plastic analysis for applied load only (Kim et al. 2006).

Fig. 18

Comparison of V factors calculated using the strip-yield (SY) model described in this paper with the R6 simplified procedure versus normalised applied stress for different magnitudes of yield stress and for a crack of length $c/R=1$

Figure 18 compares the V factors obtained by the simplified procedures in R6 and BS 7910 with those obtained using Eq. (26) for the case of tensile residual stress. The V factors predicted using Eq. (26) are much less than those estimated using the simplified procedures, suggesting these procedures result in conservative assessment outcomes. However, V factors obtained using Eq. (26) are calculated using an elastic-perfectly plastic material model while the simplified procedures make an account for hardening.

6 Conclusions

Analytical and finite element methods have been used to map the elastic behaviour of a crack in a residual stress field. Depending on the length of the crack and the magnitude of the superimposed applied stress the crack may be fully open, partially open and open at the tip, partially open but closed at the tip or fully closed. Of course, a non-zero stress intensity factor only develops when the crack is open at the tip.

Effective stress intensity factors for an elastic-perfectly plastic crack in a residual stress field under plane stress conditions have been calculated using strip yield and finite element methods with good agreement, even for high levels of applied stress approaching the yield stress. The crack opening behaviour is similar to that of an elastic crack.

Plane stress and plane strain conditions for an elastic-perfectly crack in a residual stress field have been compared using finite element analysis for a range of crack lengths and applied stresses. The effective stress intensity factors are similar except that under plane stress conditions and compressive residual stress some yielding occurs away from the crack tip leading to significantly lower stress intensity factors for shorter crack lengths.

Appendices

Appendix A: Correspondence of stress function and eigenstrain approaches for generating residual stress fields

In this appendix the eigenstrain distribution is calculated corresponding to the residual stresses produced by the stress function in the main body of the paper.

For plane axisymmetry, the total strain components, $\varepsilon _{rr}$ and $\varepsilon _{\theta \theta }$, are

$$\begin{aligned} \varepsilon _{rr}= & {} \frac{1}{E}\left( {\sigma _{rr} -\nu \sigma _{\theta \theta } } \right) +\varepsilon _{rr}^*\nonumber \\ \varepsilon _{\theta \theta }= & {} \frac{1}{E}\left( {\sigma _{\theta \theta } -\nu \sigma _{rr} } \right) +\varepsilon _{\theta \theta }^*\end{aligned}$$

(27)

where $\varepsilon _{rr}^*$ and $\varepsilon _{\theta \theta }^*$ are components of the eigenstrain (DeWald and Hill 2006).

The equation of strain compatibility for plane axisymmetry is

$$\begin{aligned} r\frac{d\varepsilon _{\theta \theta } }{dr}+\varepsilon _{\theta \theta } -\varepsilon _{rr} =0 \end{aligned}$$

(28)

Substitution of the strain components from Eq. (27) into Eq. (28) provides an equation that the eigenstrain components must satisfy for the residual stress to be equivalent to those derived from the stress function of Eq. (3). For the stress components $\sigma _{rr}$ and $\sigma _{\theta \theta }$ of Eq. (2) this equation is

$$\begin{aligned}&r\left[ {\frac{\sigma _{RS} r\left( {r^{2}-4R^{2}} \right) }{R^{4}E}\exp \left[ {-\frac{r^{2}}{2R^{2}}} \right] +\frac{d\varepsilon _{rr}^*}{dr}} \right] \nonumber \\&\quad +\,\varepsilon _{\theta \theta }^*-\varepsilon _{rr}^*=0 \end{aligned}$$

(29)

Any set of eigenstrain components satisfying Eq. (29) will produce the same residual stress distribution, for example if we choose $\varepsilon _{\theta \theta }^*=\varepsilon _{rr}^*$ we obtain the solution

$$\begin{aligned} \varepsilon _{\theta \theta }^*=\varepsilon _{rr}^*=\frac{\sigma _{RS} \left( {r^{2}-4R^{2}} \right) }{R^{2}E}\exp \left[ {-\frac{r^{2}}{2R^{2}}} \right] \end{aligned}$$

(30)

Appendix B: Stress intensity factors and crack opening displacements for twin collinear cracks under point loads

This appendix presents solutions for the stress intensity factors and crack opening displacements for twin collinear cracks under point loads. These solutions are used in the main body of the paper to evaluate stress intensity factors and crack opening displacement for a crack in a compressive residual stress field. The principal reference used in this appendix is Tada et al. (2000) although the equations presented in this reference contain errors which have been corrected here. Other relevant work includes Tranter (1961), Erdogan (1962), Lowengrub and Srivastava (1968), Maiti et al. (1979) and Xu et al. (2011)

The initial case considered here is that of a concentrated force P per unit thickness applied to one of the cracks at a distance d from the centre (Fig. 19). This case is used to generate solutions for the case of two pairs of point forces presented next. The stress intensity factors are:

$$\begin{aligned} K_{\pm a}= & {} \frac{P}{2\sqrt{\pi a}\sqrt{c^{2}-a^{2}}}\left\{ \sqrt{c^{2}-d^{2}}\sqrt{\frac{d\pm a}{d\mp a}}\right. \nonumber \\&\left. +\,b\left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} \nonumber \\ K_{\pm c}= & {} \frac{P}{2\sqrt{\pi c}\sqrt{c^{2}-a^{2}}}\left\{ \pm \sqrt{d^{2}-a^{2}}\sqrt{\frac{b\pm d}{b\mp d}}\right. \nonumber \\&\left. -\,b\left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} \end{aligned}$$

(31)

where $m=1-\frac{a^{2}}{c^{2}}$, $\phi =\sin ^{-1}\sqrt{\frac{c^{2}-d^{2}}{c^{2}-a^{2}}}$.

$K\left( m \right)$ and $F\left( {\phi ,m} \right)$ are complete and incomplete elliptic integrals of the first kind. $E\left( m \right)$ and $E\left( {\phi ,m} \right)$ are complete and incomplete elliptic integrals of the second kind.

Fig. 19

A single point load applied to twin collinear cracks

The stress intensity factors for two pairs of concentrated forces (Fig. 20) can be generated by superimposition, using Eq. (31):

$$\begin{aligned} K_a= & {} \frac{2P}{\sqrt{\pi a}\sqrt{c^{2}-a^{2}}}\left\{ \frac{d\sqrt{c^{2}-d^{2}}}{\sqrt{d^{2}-a^{2}}}\right. \nonumber \\&\left. +\,c\left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} \nonumber \\ K_c= & {} \frac{2P}{\sqrt{\pi c}\sqrt{c^{2}-a^{2}}}\left\{ \frac{d\sqrt{d^{2}-a^{2}}}{\sqrt{c^{2}-d^{2}}}\right. \nonumber \\&\left. -\,c\left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} \end{aligned}$$

(32)

Fig. 20

Two pairs of point loads applied to twin collinear cracks

Figure 21 shows normalised stress intensity factors for the two crack tips versus the position of application of the point loads calculated using Eq. (32) for $a/c=0.3791$, compared with finite element results, obtained using the techniques described in the main body of the paper.

Fig. 21

Comparison of analytical and finite element calculations for normalised stress intensity factors at the tips $x=\pm a$ and $x=\pm c$ for two pairs of point loads applied at $x=\pm d$ for $a/c=0.3791$

By integration, Eq. (32) is used to find the stress intensity factors presented in Eq. (13) for twin collinear cracks in a residual stress field.

Fig. 22

Comparison of analytical and finite element calculations for the normalised crack opening displacement at $x=\pm b$ for two pairs of point loads applied at $x=\pm d$ for $a/c=0.4929$ and $d/c=0.7583$

The opening of the crack due to two pairs of concentrated forces may be evaluated from Eq. (32) using the Paris method (Tada et al. 2000). First we define $K_x^b$ as the stress intensity at x due to two pairs of unit concentrated forces applied at $\pm b$ to twin cracks, each of length $x-a$.

$$\begin{aligned} K_x^b= & {} \frac{2}{\sqrt{\pi x}\sqrt{x^{2}-a^{2}}}\left\{ \frac{b\sqrt{b^{2}-a^{2}}}{\sqrt{x^{2}-b^{2}}}\right. \nonumber \\&\left. -\,x\left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} \end{aligned}$$

(33)

where $m=1-\frac{a^{2}}{x^{2}}$ and $\phi =\sin ^{-1}\sqrt{\frac{x^{2}-b^{2}}{x^{2}-a^{2}}}$

Next we define $K_x^d$ as the stress intensity at x due to two pairs of unit concentrated forces applied at $\pm d$, again to twin cracks of length $x-a$.

$$\begin{aligned} K_x^d= & {} \frac{2}{\sqrt{\pi x}\sqrt{x^{2}-a^{2}}}\left\{ \frac{d\sqrt{d^{2}-a^{2}}}{\sqrt{x^{2}-d^{2}}}\right. \nonumber \\&\left. -\,x\left[ {\frac{E\left( m \right) F\left( {\phi ,m} \right) }{K\left( m \right) }-E\left( {\phi ,m} \right) } \right] \right\} \end{aligned}$$

(34)

where $m=1-\frac{a^{2}}{x^{2}}$ and $\phi =\sin ^{-1}\sqrt{\frac{x^{2}-d^{2}}{x^{2}-a^{2}}}$

The crack opening displacement $\delta$ at $x=\pm b$ due to two pairs of concentrated forces of magnitude P applied at $x=\pm d$ to twin cracks each of length $c-a$ (Fig. 20) is calculated by

$$\begin{aligned} \delta= & {} \frac{2P}{{E}'}\mathop \int \limits _{x=d}^c {K_x^b K_x^d dx\hbox { for }b<d} \nonumber \\ \delta= & {} \frac{2P}{{E}'}\mathop \int \limits _{x=b}^c {K_x^b K_x^d dx} \hbox { for }b>d \end{aligned}$$

(35)

Figure 22 shows normalised crack opening displacement versus distance along the crack calculated using Eq. (B7) for $a/c=0.4929$ and $d/c=0.7583$, compared with finite element results.

Equation (35) is used in the main body of the paper to find the crack opening displacements for twin collinear cracks in a residual stress field.