Skip to main content

Advertisement

SpringerLink
Log in

Anti-plane Yoffe-type crack in ferroelectric materials

  • Original Paper
  • Published:
International Journal of Fracture Aims and scope Submit manuscript

Abstract

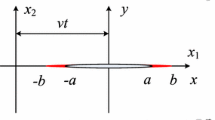
Extending the polarization saturation (PS) model and Yoffe crack model for ferroelectric materials, a moving PS model is proposed to study the problems of crack propagation considering the electrical nonlinearity. The model is solved using continuous distribution dislocation method. And the explicit expressions of the size of the electric saturation zone, intensity factors and the local energy release rate for the moving PS model are derived. It can be deducted from this model that the intensity factors and the size of the electric saturation zone are independent of the velocity of the crack. The local energy release rate for the moving PS model has the form of that for a stationary crack multiplied by the local energy release rate universal function f(v). And it increases monotonically with increasing v. When the velocity of the crack v → 0, the moving PS model will reduce to the static PS model. When the size of the electric saturation zone r → 0, the moving PS model is in agreement with the moving linear piezoelectric model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Atkinson C (1977) Dynamic crack problems in dissimilar media. In: Sih GC (ed) Mechanics of fracture, vol 4. Noordhoff International Publishing, Leyden, pp 213–248

    Google Scholar 

  • Baker BR (1962) Dynamic stresses created by a moving crack. J Appl Mech 29: 449–458

    Article  CAS  Google Scholar 

  • Barnett DM, Asaro RJ (1972) The fracture mechanics of slit-like cracks in anisotropic elastic media. J Mech Phys Solids 20: 353–366

    Article  Google Scholar 

  • Beom HG, Kim YH, Cho C, Kim CB (2006a) A crack with an electric displacement saturation zone in an electrostrictive material. Arch Appl Mech 76: 19–31

    Article  Google Scholar 

  • Beom HG, Kim YH, Cho C, Kim CB (2006b) Asymptotic analysis of an impermeable crack in an electrostrictive material subjected to electric loading. Int J Solids Struct 43: 6869–6886

    Article  Google Scholar 

  • Bilby BA, Cottrell AH, Swinden KH (1963) The spread of plastic yield from a notch. Proc R Soc A 272: 304–314

    Article  Google Scholar 

  • Broberg KB (1960) The propagation of a brittle crack. Arch fur Fysik 18: 159–192

    Google Scholar 

  • Chen XH, Ma CC, Ing YS, Tsai CH (2008) Dynamic interfacial crack propagation in elastic–piezoelectric bi-materials subjected to uniformly distributed loading. Int J Solids Struct 45: 959–997

    Article  Google Scholar 

  • Chen YH, Lu TJ (2003) Cracks and fracture in piezoelectrics. Adv Appl Mech 39: 121–215

    Article  Google Scholar 

  • Chen YH, Hasebe N (2005) Current understanding on fracture behavior of ferroelectric/piezoelectric materials. J Intell Mater Syst Struct 16: 673–687

    Article  CAS  Google Scholar 

  • Chen ZT, Yu SW (1997) Anti-plane Yoffe crack problem in piezoelectric materials. Int J Fract 84: L41–L45

    Google Scholar 

  • Chen ZT, Karihaloo BL, Yu SW (1998) A Griffith crack moving along the interface of two dissimilar piezoelectric materials. Int J Fract 91: 197–203

    Article  Google Scholar 

  • Dugdale DS (1960) Yielding of steel sheets containing slits. J Mech Phys Solids 8: 100–104

    Article  Google Scholar 

  • Fan TY (1987) Moving Dugdale model. Z Angew Math Phys 38: 630–641

    Article  Google Scholar 

  • Freund LB (1973) Crack propagation in an elastic solid subjected to general loading III stress wave loading. J Mech Phys Solids 21: 47–61

    Article  Google Scholar 

  • Freund LB (1990) Dynamic fracture mechanics. Cambridge Press, Cambridge

    Book  Google Scholar 

  • Fulton CC, Gao H (1997) Electrical nonlinearity in fracture of piezoelectric ceramics. Appl Mech Rev 50: S56–S63

    Article  Google Scholar 

  • Gao CF, Zhao MH, Tong P, Zhang TY (2004) The energy release rate and the J-integral of an electrically insulated crack in a piezoelectric material. Int J Eng Sci 42: 2175–2192

    Article  Google Scholar 

  • Gao CF, Zhao YT, Wang MZ (2001) Moving antiplane crack between two dissimilar piezoelectric media. Int J Solids Struct 38: 9331–9345

    Article  Google Scholar 

  • Gao H, Barnett DM (1996) An invariance property of local energy release rate in a strip saturation model of piezoelectric fracture. Int J Fract 79: R25–R29

    Article  Google Scholar 

  • Gao H, Zhang TY, Tong P (1997) Local and global energy release rates for an electrically yielded crack in a piezoelectric ceramic. J Mech Phys Solids 45: 491–510

    Article  CAS  Google Scholar 

  • Gol’dshtein RV (1966) On the steady motion of a crack along a straight line boundary between two joined materials. Mech Tverdogo Tela 1:94e102 (in Russian)

  • Jeong KM, Kim IO, Beom HG (2004) Effect of electric displacement saturation on the stress intensity factor for a crack in a ferroelectric ceramic. Mech Res Commun 31: 373–382

    Article  Google Scholar 

  • Kassir MK, Tse S (1983) Moving Griffith crack in an orthotropic material. Int J Eng Sci 21: 315–325

    Article  Google Scholar 

  • Kwon JH, Lee KY, Kwon SM (2000) Moving crack in a piezoelectric ceramic strip under anti-plane shear loading. Mech Res Commun 27: 327–332

    Article  Google Scholar 

  • Kwon JM, Lee KY (2001) Constant moving crack in a piezoelectric block: anti-plane problem. Mech Mater 33: 649–657

    Article  Google Scholar 

  • Kuna M (2010) Fracture mechanics of piezoelectric materials—where are we right now?. Eng Fract Mech 77: 309–326

    Article  Google Scholar 

  • Lapusta Y, Komarov A, Labesse-Jied F, Pitti RMoutou, Loboda V (2011) Limited permeable crack moving along the interface of a piezoelectric bi-material. Eur J Mech A-Solid 30: 639–649

    Article  Google Scholar 

  • Li S, Mataga PA (1996a) Dynamic crack propagation in piezoelectric materials-part I. Electrode solution. J Mech Phys Solids 44: 1799–1830

    Article  CAS  Google Scholar 

  • Li S, Mataga PA (1996b) Dynamic crack propagation in piezoelectric materials-part II. Vacuum solution. J Mech Phys Solids 44: 1831–1866

    Article  CAS  Google Scholar 

  • Li XF, Fan TY, Wu XF (2000) A moving mode-III crack at the interface between two dissimilar piezoelectric materials. Int J Eng Sci 38: 1219–1234

    Article  CAS  Google Scholar 

  • Li XF (2003) Griffith crack moving in a piezoelectric strip. Arch Appl Mech 72: 745–758

    Article  Google Scholar 

  • Loewy RG (1997) Recent developments in smart structures with aeronautical applications. Smart Mater Struct 6: 11–42

    Article  Google Scholar 

  • Loboda V, Lapusta Y, Govorukha V (2008) Mechanical and electrical yielding for an electrically insulated crack in an interlayer between piezoelectric materials. Int J Eng Sci 46: 260–272

    Article  CAS  Google Scholar 

  • Park SB, Sun CT (1995) Effect of electric fields on fracture of piezoelectric ceramics. Int J Fract 70: 203–216

    Article  Google Scholar 

  • Piva A (1986) Elastodynamic crack problems in an anisotropic medium through a complex variable approach. Q Appl Math 44: 441–445

    Google Scholar 

  • Piva A, Viola E (1988) Crack propagating in an orthotropic medium. Eng Fract Mech 29: 535–548

    Article  Google Scholar 

  • Ru CQ (1999) Effect of electrical polarization saturation on stress intensity factors in a piezoelectric ceramic. Int J Solids Struct 36: 869–883

    Article  Google Scholar 

  • Ru CQ, Mao X (1999) Conducting crack in a piezoelectric ceramics of limited electrical polarization. J Mech Phys Solids 47: 2125–2146

    Article  CAS  Google Scholar 

  • Rubio Gonzalez C, Mason J (2000) Dynamic stress intensity factors at the tip of a uniformly loaded semiinfinite crack in an orthotropic material. J Mech Phys Solids 48: 899–925

    Article  CAS  Google Scholar 

  • Rubio Gonzalez C, Mason J (2001) Dynamic stress intensity factor for a propagating crack in orthotropic materials. Int J Eng Sci 39: 15–38

    Article  Google Scholar 

  • Shen SP, Nishioka T, Hu SL (2000a) Crack propagation along the interface of piezoelectric biomaterial. Theor Appl Fract Mech 34: 185–203

    Article  CAS  Google Scholar 

  • Shen SP, Kuang ZB, Nishioka T (2000b) Dynamic mode-III interfacial crack in ferroelectric materials. Int J Appl Electromagn 11: 211–222

    Google Scholar 

  • Soh AK, Liu JX, Lee KL, Fang DN (2002) On a moving Griffith crack in anisotropic piezoelectric solids. Arch Appl Mech 72: 458–469

    Article  Google Scholar 

  • Tsai CH, Ma CC (1997a) Transient analysis of a propagating in-plane crack in a finite geometry body subjected to static loadings. J Appl Mech 64: 620–628

    Article  Google Scholar 

  • Tsai CH, Ma CC (1997b) Theoretical transient analysis of the interaction between a dynamically propagating in-plane crack and traction free boundaries. J Appl Mech 64: 819–827

    Article  CAS  Google Scholar 

  • To AC, Li S, Glaser SD (2006) Propagation of a mode-III interfacial conductive crack along a conductive interface between two piezoelectric materials. Wave Motion 43: 368–386

    Article  Google Scholar 

  • Wang X, Zhong Z, Wu FL (2003) A moving conducting crack at the interface of two dissimilar piezoelectric materials. Int J Solids Struct 40: 2381–2399

    Article  Google Scholar 

  • Wang TC (2000) Analysis of strip electric saturation model of crack problem in piezoelectric materials. Int J Solids Struct 37: 6031–6049

    Article  Google Scholar 

  • Willis JR (1971) Fracture mechanics of interfacial cracks. J Mech Phys Solids 19: 353–368

    Article  Google Scholar 

  • Willis JR (1973) Self-similar problems in elastodynamics. Philos Trans R Soc Lond 272: 435–491

    Google Scholar 

  • Wu KC (1989) On the crack-tip fields of a dynamically propagating crack in anisotropic elastic solid. Int J Fract 41: 253–266

    Article  CAS  Google Scholar 

  • Wu KC (1991) Explicit crack tip fields of an extending interface crack in an anisotropic biomaterial. Int J Solids Struct 27: 455–466

    Article  Google Scholar 

  • Yang W, Suo Z, Shih CF (1991) Mechanics of dynamic debonding. Proc R Soc Lond A 433: 679–697

    Article  Google Scholar 

  • Yoffe EH (1951) The moving Griffith crack. Philos Mag 42: 739–750

    Google Scholar 

  • Zhang TY, Zhao MH, Tong P (2002) Fracture of piezoelectric ceramics. Adv Appl Mech 38: 147–289

    Article  Google Scholar 

  • Zhang TY, Gao CF (2004) Fracture behaviors of piezoelectric materials. Theor Appl Fract Mech 41: 339–379

    Article  CAS  Google Scholar 

  • Zhang TY, Zhao MH, Cao CF (2005) The strip dielectric breakdown model. Int J Fract 132: 311–327

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Tsinghua University, Beijing, 100084, China

    Hao-sen Chen

  2. LTCS, College of Engineering, Peking University, Beijing, 100871, China

    Jing Ma, Yong-mao Pei & Dai-ning Fang

Authors
  1. Hao-sen Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jing Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yong-mao Pei
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Dai-ning Fang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dai-ning Fang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chen, Hs., Ma, J., Pei, Ym. et al. Anti-plane Yoffe-type crack in ferroelectric materials. Int J Fract 179, 35–43 (2013). https://doi.org/10.1007/s10704-012-9767-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10704-012-9767-2

Keywords

Search

Navigation