Skip to main content
SpringerLink
Log in

Generalised stress intensity factors for rounded notches in plates under in-plane shear loading

  • Original Paper
  • Published:
International Journal of Fracture Aims and scope Submit manuscript

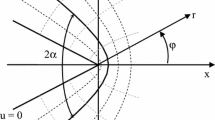
Abstract

The Notch Stress Intensity Factors (NSIFs) quantify the intensities of the asymptotic linear elastic stress distributions of sharp (zero radius) V-shaped notches. When the notch tip radius is different from zero, the singular sharp-notch field diverges from the rounded-notch solution in the close neighborhood of the notch tip. Nevertheless the NSIFs might continue to be parameters governing fracture if the notch root radius is small enough. Otherwise they can be seen simply as stress field parameters useful in quantifying the stress distributions ahead of the specific notch. Taking advantage of some analytical formulations which are able to describe stress distributions ahead of parabolic, hyperbolic and V-shaped notches with end holes, the paper discusses the form and the significance of the NSIFs with reference to in-plane shear loading, considering explicitly the role played by the notch opening angle and the notch tip radius. These parameters quantify the stress redistribution due to the root radius with respect to the sharp notch case to which they should naturally tend for decreasing values of the notch radius.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Atzori B, Lazzarin P (2001) Notch sensitivity and defect sensitivity: two sides of the same medal. Int J Fract 107: L3–L8

    Article  Google Scholar 

  • Atzori B, Lazzarin P, Meneghetti G (2003) Fracture mechanics and notch sensitivity. Fatigue Fract Eng Mater Struct 26: 257–267

    Article  Google Scholar 

  • Atzori B, Lazzarin P, Tovo R (1999) Stress field parameters to predict the fatigue strength of notched components. J Strain Anal 34: 437–453

    Article  Google Scholar 

  • Atzori B, Lazzarin P, Tovo R (1999) From the local stress approach to fracture mechanics: a comprehensive evaluation of the fatigue strength of welded joints. Fatigue Fract Eng Mater Struct 22: 369–382

    Article  CAS  Google Scholar 

  • Ayatollahi MR, Aliha MRM (2009) Analysis of a new specimen for mixed mode fracture tests on brittle materials. Eng Fract Mech 76: 1563–1573

    Article  Google Scholar 

  • Ayatollahi MR, Dehghany M (2010) On T-stresses near V-notches. Int J Fract 165: 121–126

    Article  Google Scholar 

  • Ayatollahi MR, Torabi AR (2010) Investigation of mixed mode brittle failure in rounded-tip V-notches components. Eng Fract Mech 2010(77): 3087–3104

    Article  Google Scholar 

  • Ayatollahi MR, Torabi AR (2011) Failure assessment of notched polycrystalline graphite under tensile-shear loading. Mater Sci Eng. doi:10.1016/j.msea.20121.04.066 (in press)

  • Ayatollahi MR, Nejati M (2011) Determination of NSIFs and coefficients of higher order terms for sharp notches using finite element method. Int J Mech Sci. doi:10.1016/j.ijmecsci.2010.12.005 (in press)

  • Benthem JP (1987) Stresses in the region of rounded corners. Int J Solids Struct 23: 239–252

    Article  Google Scholar 

  • Berto F, Lazzarin P, Gomez FJ, Elices M (2007) Fracture assessment of U-notches under mixed mode loading: Two procedures based on the ‘equivalent local mode I’ concept. Int J Fract 148: 415–433

    Article  CAS  Google Scholar 

  • Berto F, Lazzarin P, Harding S, Kotousov A (2011) Out-of-plane singular stress fields in V-notched plates and welded lap joints induced by in-plane shear load conditions. Fatigue Fract Eng Mater Struct 34: 291–304

    Article  Google Scholar 

  • Boukharouba T, Tamine T, Nui L, Chehimi C, Pluvinage G (1995) The use of notch stress intensity factor as a fatigue crack initiation parameter. Eng Fract Mech 52: 503–512

    Article  Google Scholar 

  • Carpinteri A, Cornetti P, Pugno N, Sapora A (2010) On the most dangerous V-notch. Int J Solids Struct 47: 887–893

    Article  Google Scholar 

  • Chen DH (1995) Stress intensity factors for V-notched strip under tension or in-plane bending. Int J Fract 70: 81–97

    Article  Google Scholar 

  • Cheng YZ (1988) Evaluation of K2 values from the solution of notch problem. Int J Fract 38: R61–64

    Google Scholar 

  • Creager M, Paris PC (1967) Elastic field equations for blunt cracks with reference to stress corrosion cracking. Int J Fract Mech 3: 247–252

    CAS  Google Scholar 

  • Dini D, Hills D (2004) Asymptotic characterisation of nearly-sharp notch root stress fields. Int J Fract 130: 651–666

    Article  Google Scholar 

  • Dunn ML, Suwito W, Cunningham S (1997a) Fracture initiation at sharp notches: correlation using critical stress intensities. Int J Solids Struct 34: 3873–3883

    Article  Google Scholar 

  • Dunn ML, Suwito W, Cunningham S, May CW (1997b) Fracture initiation at sharp notches under mode I, mode II, and mild mixed mode loading. Int J Fract 84: 367–381

    Article  CAS  Google Scholar 

  • Filippi S, Lazzarin P, Tovo R (2002) Developments of some explicit formulas useful to describe elastic stress fields ahead of notches in plates. Int J Solids Struct 39: 4543–4565

    Article  Google Scholar 

  • Glinka G (1985) Calculation of inelastic notch-tip strain-stress histories under cyclic loading. Eng Fract Mech 22: 839–854

    Article  Google Scholar 

  • Gogotsi GA (2003) Fracture toughness of ceramics and ceramic composites. Ceram Int 7: 777–884

    Article  Google Scholar 

  • Gómez FJ, Elices M (2003) A fracture criterion for sharp V-notched samples. Int J Fract 123: 163–175

    Article  Google Scholar 

  • Gómez FJ, Elices M (2004) A fracture criterion for blunted V-notched samples. Int J Fract 127: 239–264

    Article  Google Scholar 

  • Gómez FJ, Guinea GV, Elices M (2006) Failure criteria for linear elastic materials with U-notches. Int J Fract 141: 99–113

    Article  Google Scholar 

  • Gómez FJ, Elices M (2006) Fracture loads for ceramic samples with rounded notches. Eng Fract Mech 73: 880–894

    Article  Google Scholar 

  • Gómez FJ, Elices M, Berto F, Lazzarin P (2007) Local strain energy density to assess the static failure of U-shaped notches in plates under mixed mode loading. Int J Fract 145: 29–45

    Article  Google Scholar 

  • Gómez FJ, Elices M, Berto F, Lazzarin P (2008) A generalised notch stress intensity factor for U-notched components under mixed mode. Eng Fract Mech 75: 4819–4833

    Article  Google Scholar 

  • Gómez FJ, Elices M, Berto F, Lazzarin P (2009) Fracture of V-notched specimens under mixed mode (I+II) loading in brittle materials. Int J Fract 159: 121–135

    Article  Google Scholar 

  • Gross R, Mendelson A (1972) Plane elastostatic analysis of V-notched plates. Int J Fract Mech 8: 267–276

    Article  Google Scholar 

  • Harding S, Kotousov A, Lazzarin P, Berto F (2010) Transverse singular effects in V-shaped notches stressed in mode II. Int J Fract 164: 1–14

    Article  Google Scholar 

  • Irwin GR (1958). Fracture. In: Handbuch der Physik 6. Springer, Berlin, pp 551–590

  • Knésl Z (1991) A criterion of V-notch stability. Int J Fract 48: R79–R83

    Article  Google Scholar 

  • Kotousov A, Lew TL (2006) Stress singularities resulting from various boundary conditions in angular corners of plates of arbitrary thickness in extension. Int J Solids Struct 43: 5100–5109

    Article  Google Scholar 

  • Kotousov A (2007) Fracture in plates of finite thickness. Int J Solids Struct 44: 8259–8273

    Article  Google Scholar 

  • Kotousov A, Lazzarin P, Berto F, Harding S (2010) Effect of the thickness on elastic deformation and quasi-brittle fracture of plate components. Eng Fract Mech 77: 1665–1681

    Article  Google Scholar 

  • Lazzarin P, Tovo R (1996) A unified approach to the evaluation of linear elastic stress fields in the neighborhood of cracks and notches. Int J Fract 78: 3–19

    Article  Google Scholar 

  • Lazzarin P, Tovo R (1998) A notch intensity approach to the stress analysis of Welds. Fatigue Fract Eng Mater Struct 21: 1089–1104

    Article  CAS  Google Scholar 

  • Lazzarin P, Filippi S (2006) A generalised stress intensity factor to be applied to rounded V-shaped notches. Int J Solids Struct 43: 2461–2478

    Article  Google Scholar 

  • Lazzarin P, Zappalorto M, Yates JR (2007) Analytical study of stress distributions due to semi-elliptic notches in shafts under torsion loading. Int J Eng Sci 45: 308–328

    Article  CAS  Google Scholar 

  • Leguillon D, Yosibash Z (2003) Crack onset at a V-notch. Influence of the notch tip radius. Int J Fract 122: 1–21

    Article  CAS  Google Scholar 

  • Leguillon D, Quesada D, Putot C, Martin E (2007) Prediction of crack initiation at blunt notches and cavities—size effects. Eng Fract Mech 74: 2420–2436

    Article  Google Scholar 

  • Muskhelishvili NI (1977) Some basic problems of the mathematical theory of elasticity, 4th edn. Noordhoof International, Leyden

    Google Scholar 

  • Nakamura T, Parks DM (1989) Antisymmetrical 3-D stress field near the crack front of a thin elastic plate. Int J Solids Struct 25: 1411–1426

    Article  Google Scholar 

  • Neuber H (1958) Kerbspannungslehre 2nd edn. Springer-Verlag, Berlin

    Google Scholar 

  • Noda N, Takase Y (2003) Generalized stress intensity factors for V-shaped notch in a round bar under torsion, tension and bending. Eng Fract Mech 70: 1447–1466

    Article  Google Scholar 

  • Nui LS, Chehimi C, Pluvinage G (1994) Stress field near a large blunted tip V-notch and application of the concept of the critical notch stress intensity factor (NSIF) to the fracture toughness of very brittle materials. Eng Fract Mech 49: 325–335

    Article  Google Scholar 

  • Pook LP (2000) Finite element analysis of corner point displacements and stress intensity factors for narrow notches in square sheets and plates. Fatigue Fract Eng Mater Struct 23: 979–992

    Article  Google Scholar 

  • Priel E, Bussiba A, Gilad I, Yosibash Z (2007) Mixed mode failure criteria for brittle elastic V-notched structures. Int J Fract 144: 247–265

    Article  CAS  Google Scholar 

  • Radaj D, Zhang S (1993) On the relations between notch stress and crack stress intensity in plane shear and mixed mode loading. Eng Fract Mech 44: 691–704

    Article  Google Scholar 

  • Savruk MP, Kazberuk A (2006) A Relationship between the stress intensity and stress concentration factors for sharp and rounded notches. Mater Sci 42: 725–738

    Article  Google Scholar 

  • Savruk MP, Kazberuk A (2010) A two-dimensional fracture mechanics problems for solids with sharp and rounded V-notches. Int J Fract 161: 79–95

    Article  Google Scholar 

  • Seweryn A, Molski K (1996) Elastic stress singularities and corresponding generalized stress intensity factors for angular corners under various boundary condition. Eng Fract Mech 55: 529–556

    Article  Google Scholar 

  • Sih GC, Liebowitz H (1968) Mathematical theories of brittle fracture. In fracture, vol II. Mathematical fundamentals. Academic Press, London, UK

    Google Scholar 

  • Strandberg M (1999) A numerical study of the elastic stress field arising from sharp and blunt V-notches in a SENT-specimen. Int J Fract 100: 329–342

    Article  Google Scholar 

  • Strandberg M (2001) Upper bounds for the notch intensity factor for some geometries and their use in general interpolation formulae. Eng Fract Mech 68: 577–585

    Article  Google Scholar 

  • Verreman Y, Nie B (1996) Early development of fatigue cracking at manual fillet welds. Fatigue Fract Eng Mater Struct 19: 669–681

    Article  CAS  Google Scholar 

  • Westergaard HM (1939) Bearing pressures and cracks. J Appl Mech 6: A49–A53

    Google Scholar 

  • Williams ML (1952) Stress singularities resulting from various boundary conditions in angular corners of plate in extension. J Appl Mech 19: 526–528

    Google Scholar 

  • Zappalorto M, Lazzarin P, Yates JR (2008) Elastic stress distributions resulting from hyperbolic and parabolic notches in round shafts under torsion and uniform antiplane shear loadings. Int J Solids Struct 45: 4879–4901

    Article  Google Scholar 

  • Zappalorto M, Lazzarin P, Berto F (2009) Elastic notch stress intensity factors for sharply V-notched rounded bars under torsion. Eng Fract Mech 76: 439–453

    Article  Google Scholar 

  • Zappalorto M, Lazzarin P, Filippi S (2010) Stress field equations for U and blunt V-shaped notches in axisymmetric shafts under torsion. Int J Fract 164: 253–269

    Article  Google Scholar 

  • Zappalorto M, Lazzarin P (2011) In-plane and out-of-plane stress field solutions for V-notches with end holes. Int J Fract 168: 167–180

    Article  Google Scholar 

  • Zhao Z, Hahn HG (1992) Determining the SIF of a V-notch from the results of a mixed-mode crack. Eng Fract Mech 43: 511–518

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Management and Engineering, University of Padova, Stradella San Nicola 3, 36100, Vicenza, Italy

    P. Lazzarin, M. Zappalorto & F. Berto

Authors
  1. P. Lazzarin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Zappalorto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. F. Berto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. Lazzarin.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lazzarin, P., Zappalorto, M. & Berto, F. Generalised stress intensity factors for rounded notches in plates under in-plane shear loading. Int J Fract 170, 123–144 (2011). https://doi.org/10.1007/s10704-011-9613-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10704-011-9613-y

Keywords

Search

Navigation