Skip to main content
SpringerLink
Log in

Determination of Second-Order term Coefficients for the Inclined Crack in Orthotropic Plate using Singular Finite Elements

  • Letters in Fracture and Micromechanics
  • Published:
International Journal of Fracture Aims and scope Submit manuscript

Abstract

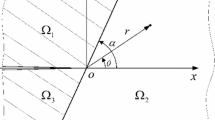
The finite element method with quarter-point crack-tip elements is used and a simple formula for obtaining the coefficients of the second-order terms in the series expansion for near crack tip stresses in orthotropic materials under biaxial loading is presented. This formula is obtained by comparing the variation of the displacements along the crack tip element with the elastic field solution for the crack tip. Numerical examples are given for the validity of the present formulation. The results obtained are compared with the theoretical ones and a good agreement between the two solutions is obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Boone TJ, Wawrzynek WA, Ingraffea AR: Finite element modelling of fracture propagation in orthotropic materials. Engng Fract Mech 26(2), 185–201 (1987)

    Article  Google Scholar 

  • Bowie OL, Freese CE: Central crack in plane orthotropic rectangular sheet. Int J Fract Mech 8(1), 49–58 (1972)

    Article  Google Scholar 

  • Carloni C, Nobile L (2002). Crack initiation behavior of orthotropic solids as predicted by the strain energy density theory. Theor Appl Fract Mech 38, 109-19.

    Google Scholar 

  • Carloni C, Piva A, Viola E (2003). An alternative complex variable formulation for an inclined crack in an orthotropic medium. Engng Fract Mech 70, 2033-58.

    Google Scholar 

  • FRANC2D (2007). Cornell Fracture Group. Available from: www.cfg.cornell.edu.

  • Garcia F, Saez A, Dominguez J (2004). Traction boundary elements for cracks in anisotropic solids. Boundary Analysis with Boundary Elements 28: 667-76.

    Google Scholar 

  • Lim WK, Choi SY, Sankar BV (2001). Biaxial load effects on crack extension in anisotropic solids. Engng Fract Mech 68, 403-16.

    Google Scholar 

  • Lim WK, Sankar BV (2002). Non-singular term effect for the inclined crack extension in anisotropic solids under uniaxial loading. J Compos Mater 36(17), 2031-44.

    Google Scholar 

  • Nobile L, Carloni C (2005). Fracture analysis for orthotropic cracked plates. Composite Structures 68, 285-93.

    Google Scholar 

  • Nobile L, Piva A, Viola E (2004). On the inclined crack problem in an orthotropic medium under biaxial loading. Engng Fract Mech 71, 529-46.

    Google Scholar 

  • Saouma VE, Sijiotis ES (1986). Stress intensity factors in anisotropic bodies using singular isoparametric elements. Engng Fract Mech 25, 115-21.

    Google Scholar 

  • Savin GN: Stress concentration around holes. Gordon and Breach Science Publisher, New York (1968)

    Google Scholar 

  • Sih, GC, Liebowitz H (1968). Mathematical theories of brittle fracture in fracture mechanics, In:Liebowitz H ed. Fracture mechanics, vol.II. New York: Academic Press; 108-30.

  • Viola E, Boldrini C, Tornabene F (2008). Non-singular term effect on the fracture quantities of a crack in a piezoelectric medium. Engng Fract Mech 75, 4542-67.

    Google Scholar 

  • Yang S, Yuan FG: Determination and representation of the stress coefficient terms by path-independent integrals in anisotropic cracked solids. Int J Fract 101(4), 291–319 (2000)

    Article  Google Scholar 

  • Yang S, Yuan FG (2000b). Kinked crack in anisotropic bodies. Int J Solids Struct 37, 6635-82.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, MyongJi University, Yongin, Gyonggi-do, 449-728, Republic of Korea

    Won-Kyun Lim

Authors
  1. Won-Kyun Lim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Won-Kyun Lim.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lim, WK. Determination of Second-Order term Coefficients for the Inclined Crack in Orthotropic Plate using Singular Finite Elements. Int J Fract 168, 125–132 (2011). https://doi.org/10.1007/s10704-010-9569-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10704-010-9569-3

Keywords

Search

Navigation