Abstract
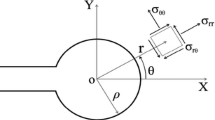
In this study, a method of evaluating the static strength of a V-shaped notch based on the singular stress field at the notch tip is studied. The singular stress fields is defined by two parameters, \({K_{I, \lambda_1}}\) and \({K_{II,\lambda_2}}\) , which correspond to the intensities of symmetric stress field and the skew-symmetric field, respectively. Four kinds of fracture criteria are considered; two of them are based on the tensile strength σ B and the other two are based on the fracture toughness K IC . The usefulness of the criteria is investigated through the experimental results carried out on plane specimens of acrylic resin having a sharp notch for various notch configurations such as the opening angle, the inclined angle and the notch depth. It is shown that the criteria using stress intensity factor and the energy release rate not sensitive to the length of the virtual crack \({\varepsilon}\) .
Similar content being viewed by others
References
Chen DH (1995) Stress intensity factors for V-notched strip under tension or in-plane bending. Int J Fract 70: 81–97
Chen DH, Nisitani H (1997) Body force method. Int J Fract 86: 161–189
Chen DH, Noda NA, Takase Y, Morotomi T (1996) Evaluation of static strength by the application of stress intensity of angular corner. Trans JSME 62(598): 1445–1449 (in Japanese)
Dunn ML, Suiwito W, Cunningham SJ (1997) Fracture initiation at sharp notches under mode I, mode II, and mild mixed mode loading. Int J Fract 84: 367–381
Erdogan F, Sih GC (1963) On the crack extension in plates under plane loading and transverse shear. Trans ASME J Basic Eng 85: 519–527
Gomez FJ, Elices M (2003) A fracture criterion for sharp V-notched samples. Int J Fract 123: 163–175
Gomez FJ, Elices M (2004) A fracture criterion for blunted V-notched samples. Int J Fract 127: 239–264
Gomez FJ, Guinea GV, Elices M (2006) Failure criteria for linear elastic materials with U-notches. Int J Fract 141: 99–113
Grenestedt JL, Hallstrom S, Kuttenkeuler J (1996) On cracks emanating from wedges in expanded PVC foam. Eng Fract Mech 54: 445–456
Hallstrom S, Grenestedt JL (1997) Mixed mode fracture of cracks and wedge shaped notches in expanded PVC foam. Int J Fract 88: 343–358
Hattori T, Sakata S, Hatsuda T, Murakami G (1988) A stress singularity parameters approach for evaluating adhesive strength. Trans JSME 54(499): 597–603 (in Japanese)
Hussain MA, Pu SL, Underwood J (1974) Strain energy release rate for a crack under combined Mode-I and -II, vol 560. ASTM STP, Philadelphia, pp 2–28
Lazzarin P, Tovo R (1996) A unified approach to the evaluation of linear elastic stress fields in the neighbourhood of crack and notches. Int J Fract 78: 3–19
Leblond JB, Mouro P (1999) Crack propagation from a preexisting flaw at a notch root.Endommagement, fatigue, rupture/Damage, fatigue, rupture. C R Acad Sci Paris t 327;Sbrie II 6: 581–587
Leguillon D (2002) Strength or toughness? A criterion for crack onset at a notch. Eur J Mech A: Solids 21: 61–72
Leguillon D, Quesada A, Putot C, Martin E (2007) Prediction of crack initiation at blunt notches and cavities—size effects. Eng Fract Mech 74: 2420–2436
Nisitani N, Chen DH, Isida M (1984) An approximate method for calculating KI and KII of various edge cracks emanating from the apex of an elliptic hole. Trans JSME 50(451): 519–527 (in Japanese)
Noda NA, Chen DH, Takase Y, Morotomi T (1998) Evaluation of static strength by the application of mixed mode stress intensity of angular corner. Trans JSME 64(620): 958–963 (in Japanese)
Noda NA, Kouyama T, Kinoshita Y (2006) Stress intensity factors of an inclined elliptical crack near a bimaterial interface. Eng Fract Mech 73: 1292–1320
Nuismer RJ (1975) An energy release rate criterion for mixed mode fracture. Int J Fract 11: 245–250
Palaniswamy K, Knauss EG (1972) Propagation of a crack under general in-plane tension. Int J Fract 8: 114–117
Pook LP (2000) Linear elastic fracture mechanics for engineers. WIT Press, Boston
Severyn A (1994) Brittle fracture criterion for structures with sharp notches. Eng Fract Mech 47: 673–681
Severyn A, Poskrobko S, Mroz Z (1997) Brittle fracture in plane elements with sharp notches under mixed-mode loading. J Eng Mech 123: 535–543
Seweryn A, Lukaszewicz A (2002) Verification of brittle fracture criteria for elements with V-shaped notches. Eng Fract Mech 69: 1487–1510
Wang TC (1978) Fracture criteria for combined mode cracks. Sci Sin 21: 457–474
Williams ML (1952) Stress singularities resulting from various boundary conditions in angular corners of plates in extension. Trans ASME J Appl Mech 19: 526–528
Yosibash Z, Bussiba A, Gilad I (2004) Failure criteria for brittle elastic materials. Int J Fract 125: 307–333
Yosibash Z, Priel E, Leguillon D (2006) A failure criteria for brittle elastic materials under mixed-mode loading. Int J Fract 141: 291–312
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chen, D.H., Ozaki, S. Investigation of failure criteria for a sharp notch. Int J Fract 152, 63–74 (2008). https://doi.org/10.1007/s10704-008-9272-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-008-9272-9