Abstract
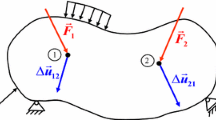
For defects in solids, when displaced within the material, reciprocity relations have been established recently similar to the theorems attributed to Betti and Maxwell. These theorems are applied to crack- and defect-interaction problems.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Barber JR (2002). Elasticity, 2nd edn. Kluwer, Dordrecht
Budiansky B and Rice J (1973). Conservation laws and energy-release rates. ASME J Appl Mech 40: 201–203
Erdogan F (1962) On the stress distribution in plates with collinear cuts under arbitrary loads. In: Proceedings of the Fourth U.S. National Congress of Applied Mechanics. ASME 1:547–553
Gross D (1982). Spannungsintensitätsfaktoren von Rißsystemen. Ing Arch 51: 301–310
Günther W (1962). Über einige Randintegrale der Elastomechanik. Abh Braunschw Wiss Ges 14: 53–72
Gurson AL (1977). Continuum theory of ductile rupture by void nucleation and growth. Part I—yield criteria and flow rules for porous ductile media. J Eng Mater Tech 99: 2–15
Gurtin ME (2000). Configurational forces as basic concepts of continuum physics. Springer, New York
Herrmann G and Kienzler R (2007a). Reciprocity relations in Eshelbian mechanics. Mech Res Commun 34: 338–343
Herrmann G, Kienzler R (2007b) A reciprocity relation couples Newtonian and Eshelbian Mechanics. ASME J Appl Mech (in press)
Kienzler R and Herrmann G (2000). Mechanics in material space. Springer, Berlin
Kienzler R, Herrmann G (2007) Nonlinear and linearized reciprocity relations in structural configurational mechanics. Acta Mech doi: 1007/s00707-007-0457-5
Kienzler R and Kordisch H (1990). Calculation of J 1 and J 2, using the L and M integral. Int J Fract 43: 213–225
Knowles JK and Sternberg E (1972). On a class of conservation laws in linearized and finite elastostatics. Arch Rat Mech Anal 44: 187–211
Marguerre K (1962) Elasticity, basic concepts. In: Flügge W Handbook of engineering mechanics. McGraw-Hill, New York
Maugin GA (1993). Material inhomogeneities in elasticity. Chapman & Hall, London
Panasyuk MP, Savruk MP and Datsyshyn AP (1977). A general method of solution of two-dimensional problems in the theory of cracks. Eng Fract Mech 9: 481–497
Rice JR (1968). A path independent integral and the approximate analysis of strain concentration by notches and cracks. ASME J Appl Mech 27: 379–386
Rohde L and Kienzler R (2005). Numerical computation and analytical estimation of stress-intensity factors for strips with multiple edge cracks. Arch Appl Mech 74: 846–852
Rohde L, Kienzler R and Herrmann G (2005). On a new method for calculating stress-intensity factors of multiple edge cracks. Phil Mag 85: 4231–4244
Schweins G (1849). Fliehmomente oder die Summe (xX + yY) bei Kräften in der Ebene und (xX + yY + zZ) bei Kräften im Raume. Crelles J Reine Angew Math 38: 77–88
Timoshenko SP and Goodier JN (1970). Theory of elasticity, 3rd edn. McGraw-Hill, New York
Author information
Authors and Affiliations
Corresponding author
Additional information
The contents of the present paper has been developed together with Prof. Dr. Dr. h. c. George Herrmann, Stanford University, California, who passed away on January 7, 2007.
Rights and permissions
About this article
Cite this article
Kienzler, R. Reciprocity in fracture and defect mechanics. Int J Fract 147, 3–11 (2007). https://doi.org/10.1007/s10704-007-9115-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-007-9115-0