No Heading
The fundamental quantum dynamics of two interacting oscillator systems are studied in two different scenarios. In one case, both oscillators are assumed to be linear, whereas in the second case, one oscillator is linear and the other is a non-linear, angular-momentum oscillator; the second case is, of course, more complex in terms of energy transfer and dynamics. These two scenarios have been the subject of much interest over the years, especially in developing an understanding of modern concepts in quantum optics and quantum electronics. In this work, however, these two scenarios are utilized to consider and discuss the salient features of quantum behaviors resulting from the interactive nature of the two oscillators, i.e., coherence, entanglement, spontaneous emission, etc., and to apply a measure of entanglement in analyzing the nature of the interacting systems.
The Heisenberg equation for both coupled oscillator scenarios are developed in terms of the relevant reduced kinematics operator variables and parameterized commutator relations. For the second scenario, by setting the relevant commutator relations to one or zero, respectively, the Heisenberg equations are able to describe the full quantum or classical motion of the interaction system, thus allowing us to discern the differences between the fully quantum and fully classical dynamical picture.
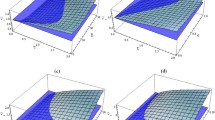
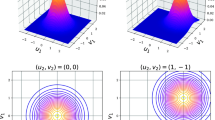
For the coupled linear and angular-momentum oscillator system in the fully quantum-mechanical description, we consider special examples of two, three, four-level angular momentum systems, demonstrating the explicit appearances of entanglement. We also show that this entanglement persists even as the coupled angular momentum oscillator is taken to the limit of a large number of levels, a limit which would go over to the classical picture for an uncoupled angular momentum oscillator.
Similar content being viewed by others
References
1. P. W. Shor, “Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer,” in Proceedings of the 35th Annual Symposium on the Foundations of Computer Science (IEEE, Los Alamitos, CA, 1994), pp. 124–134.
2. L. K. Grover, “A fast quantum mechanical algorithm for database search,” in Proceedings of the 28th Annual ACM Symposium on the Theory of Computing (ACM Press, New York, 1996), pp. 212–219.
3. I. R. Senitzky, “Nonperturbative analysis of the resonant interaction between a linear and a nonlinear oscillator,” Phys. Rev. A 3, 421 (1971).
4. J. Schwinger, Quantum Mechanics: Symbolism of Atomic Measurements, B.-G. Englert, ed. (Springer, Berlin, 2001).
5. A. Shalom and J. Zak, “A quantum mechanical model of interference,” Phys. Lett. A 43, 13 (1973).
6. G. J. Iafrate and M. Croft, “Interaction between two coupled oscillators,” Phys. Rev. A 12, 1525 (1975).
7. For a detailed discussion on general entanglement measures, see, e.g., O. Rudolph, “A new class of entanglement measures,” J. Math. Phys. 42, 5306 (2001).
8. See, e.g., D. Giulini, E. Joos, C. Kiefer, J. Kupsch, I.-O. Stamatescu, and H. D. Zeh, Decoherence and the Appearance of a Classical World in Quantum Theory (Springer, Berlin, 1996).
9. G. Mahler and V. A. Weberruss, Quantum Networks: Dynamics of Open Nanostructures, 2nd edn. (Springer, New York, 1998).
10. L. P. Hughston, R. Jozsa, and W. K. Wootters, “A complete classification of quantum ensembles having a given density matrix”, Phys. Lett. A 183, 14 (1993). In an appendix therein, it was shown that for pure states |ψ〉 of the coupled system the two reduced density matrices ^ρ(1) and ^ρ(2), have the same non-zero eigenvalues with the same multiplicities. From this we easily find that Ρ[^ρ(1)] = Ρ[^ρ(2)].
11. See, e.g., Handbook of Mathematical Functions, M. Abramowitz and I. A. Stegun, eds. (National Bureau of Standards, 1964).
12. See, e.g., W. H. Louisell, Radiation and Noise in Quantum Electronics (McGraw-Hill, New York, 1964).
13. I. R. Senitzky, “Quantum optics. III. Two-frequency interactions,” Phys. Rev. 183, 1069 (1969).
14. I. R. Senitzky, “Comment on energy balance for a dissipative system,” Phys. Rev. E 51, 5166 (1995).
15. E. T. Jaynes and F. W. Cummings, “Comparison of quantum and semiclassical radiation theories with application to the beam maser,” IEEE 51, 89 (1963).
16. In Ref. [12] pp. 212, the diagonalization of Eq. (52) for j ( ) only was described in the same basis.
17. E. Abate and H. Haken, “Exakte Behandlung eines Laser-Modells,” Z. Naturforsh. 19a, 857 (1964)
M. Tavis and F. W. Cummings, “Exact solution for an N-molecule-radiation-field Hamiltonian,” Phys. Rev. 170, 379 (1968).
D. F. Walls and R. Barakat, “Quantum-mechanical amplification and frequency conversion with a trilinear Hamiltonian,” Phys. Rev. A 1, 446 (1970).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kim, I., Iafrate, G. Entanglement in the Interaction Between Two Quantum Oscillators Systems. Found Phys Lett 17, 507–534 (2004). https://doi.org/10.1007/s10702-004-0902-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10702-004-0902-9