1 Introduction

It is well known that the universe underwent a transition from an early homogeneous phase to a late inhomogeneous one. Observational evidence of the former is given by the high degree of isotropy of the cosmic microwave background radiation (CMBR) [1] while the latter is supported by the present-day large-scale distribution of luminous matter. The observed fluctuations in the temperature of the CMBR are a reflection of density perturbations at the time of recombination, thus providing an upper bound on the amplitude of the density fluctuations at that time [2]. However, in order to explain nonlinear structures today on the scale of galaxies and clusters, we require initial perturbations. It is rather natural to assume that the perturbations start out at a very early time with a small amplitude and gradually grow in time due to gravitational instability to form the structures we observe at the present time on the scales of galaxies and galaxy clusters. The gravitational instability scenario assumes the early universe to have been almost perfectly smooth, with the exception of small density deviations with respect to the global cosmic background density. Particularly, the issue of gravitational instability of a perfect fluid with respect to small perturbations was first studied by Sir Jeans in 1902 [3, 4]. A systematic investigation of gravitational instability in a homogeneous and isotropic universe on the basis of the general theory of relativity was presented in Lifshitz’s pioneering work [5]. After that, the subject was studied by many authors. The nature of the physical mode of density perturbations is discussed from a Newtonian point of view in the textbooks by Weinberg [6], Peebles [7] and Zel’dovich and Novikov [8]. In an article in 1965, Sakharov [9] investigated the creation of astronomical bodies as a result of gravitational instability of the expanding universe. It also assumed that the initial inhomogeneities arise due to the quantum fluctuations of cold baryon-lepton matter at densities of the order of \(10^{98}\) baryons/\(cm^3\) and this initial inhomogeneities in the distribution of matter can explain the origin of the clusters. The generally accepted picture, however, is that the universe started off in an extremely homogeneous and isotropic state, with initial conditions provided by an era of accelerated expansion called inflation [10]. The tiny primordial density fluctuations, generated during inflation from quantum fluctuations of the vacuum, would later grow under the influence of gravity and eventually collapse to form the structures that we observe today, like galaxies, clusters and super-clusters. The instability of primordial density fluctuations as observed in the CMB, to grow into the present day astronomical structures is well established under Newtonian and Einstein gravity. But such a scenario can be constrained most severely by observations of cosmic microwave background radiation (CMBR) at redshift \(z=1000\). Since the perturbations in CMBR are observed to be small (\(10^{-5} - 10^{-4}\) depending on angular scales), it follows that the energy density perturbations were small compared to unity at the redshift \(z=1000\). Also the actual amplitude of the density fluctuation is much larger than what the CMB observations imply for the baryons. Indeed in a pure baryonic universe evolving under Einstein gravity, the weak coupling of baryons and photons during the recombination era will lead to Silk damping, causing the collisional propagation of radiation from overdense to underdense regions [11]. In the standard adiabatic model with just baryons, the matter power spectrum is severely suppressed on galactic scales [12]. Thus we have to consider some additional effect of non-baryonic dark matter that can accelerate the formation of the structures in the present universe because the perturbations in the dark matter are undamped during recombination. In this context, non-baryonic cold dark matter (CDM), an essential component of the concordance model (\(\Lambda \)CDM), does not interact electromagnetically nor participate in Big Bang Nucleosynthesis (BBN), and is dynamically cold in order to seed the formation of large scale structure and provides a satisfactory description of the evolution of the universe and the growth of large scale structure [13]. But the drawback of the concordance model is that despite considerable effort, this model does not at present provide a satisfactory description of small scale structure and the dynamics of bound objects like individual galaxies. In the small scale scenario the Modified Newtonian Dynamics (MOND), proposed and introduced as an empirical law by Milgrom [14], provides reasonable descriptions of the dynamics in galaxies in the limit of low acceleration below an acceleration constant \(a_{c0}\), where dynamics become scale invariant. The MOND is used to describe the motion of bodies in a gravitational field (of a galaxy, say), the observational results are reproduced without invoking any hidden mass. However, MOND suffers a missing mass problem in groups and clusters of galaxies. The mass budget of rich clusters of galaxies works out better in \(\Lambda \)CDM than in MOND. On galaxy scales, the opposite is true. Neither theory is completely satisfactory at the group scale [13]. Thus as a mathematical description of the effective force law, MOND works remarkably well in individual galaxies. As a modified gravity theory (at the classical level), it makes some predictions that are both unique and challenging to reproduce in the context of the \(\Lambda \)CDM paradigm. However, although MOND faces sharp challenges, particularly with cosmology and in rich clusters of galaxies, the range of astrophysical problems treated under the MOND hypothesis [14] increased significantly [15, 16]. The velocity dispersion measurements for stars in the local dwarf spheroidal galaxies, the extended and flat rotation curves of spiral galaxies, the large dispersion velocities of galaxies in clusters, the gravitational lensing due to massive clusters of galaxies, and even the cosmologically inferred matter content for the universe, have been successfully modeled under MOND theory [17,18,19]. For the particular case of the structure formation the MOND and dark matter specially the \(\Lambda CDM\) can be treated as complementary to each other and when one makes a clear prediction the other tends to be mute [13]. But the dynamics of clusters and Bullet cluster tell us that MOND still requires a small fraction of massive neutrinos [17,18,19,20]. These important results are not only the indirect evidences for the existence of a dominant dark matter component, but also direct evidence for the failure of the Newtonian and general relativistic theories of gravity in the large scale or low acceleration regimes relevant for the above astrophysical problems [21]. As MOND requires some form of dark matter to explain the bullet cluster observations or the the CMB observation, there are no clear boundary between the MOND and the dark matter models. In the context of models of modified gravity, Calmet and Kuntz [22] have shown that any theory which depends on the curvature invariants is equivalent to general relativity in the presence of new fields that are gravitationally coupled to the energy momentum tensor and conclude that any attempt to modify the Einstein-Hilbert action, preserving the underlying symmetry, leads to new degrees of freedom, i.e., new particles. In that sense, this is not different from including new matter fields by hand in the matter sector that are coupled gravitationally to the standard model matter fields. An important fact to note is that all our observational input and constraints on MOND come from systems that are controlled by gravity. MOND might constitute a modification of gravity alone, and its effects on other (‘matter’) degrees of freedom might enter only through their interaction with gravity [23]. Thus modified gravity models always include some new fields, whether one considers this to be a dark matter model or a modification of gravity lies in the eye of the beholder [22].

It has been tried by many authors to modify the gravitational law to avoid the contribution of dark matter towards the structure formation. Different kind of modifications have been proposed but the most successful which survived through observational test is the MOND and succeeds in explaining the properties of an impressively large number of objects without invoking the presence of the dark matter [24]. Once a portion of universe enters into the low acceleration region i.e. MOND regime the formation of structure becomes fast and furious as shown in the work of McGaugh [13]. He has shown a comparison of structure formation at different redshift values viz (\(z=5,\,3,\,0\) for \(\Lambda CDM\) and \(z=10,\,5,\,3 \) for MOND) by simulation according to the MLAPM N-body code. From this comparison it is clear that the structure formation under MONDian scenario goes faster than \(\Lambda CDM\). In the cosmological density perturbation theory, Nusser [25] studied the implication of MOND on the large-scale structure in a Friedmann-Robertson-Walker universe and employed a ‘Jeans swindle’ to write a MOND-type relationship between the fluctuations in the density and the gravitational force, g. In an another article, Nusser and Pointecouteau [26] use a one-dimensional hydrodynamical code to study the evolution of spherically symmetric perturbations in the framework of MOND. The code evolves spherical gaseous shells in an expanding Universe by employing a MOND-type relationship between the fluctuations in the density field and the gravitational force, g. Thus the use of MONDian theory to study and analysis relating cosmological density perturbations is not completely new. But the application of symmetry-based approach is not common topic used in cosmological structure formation theory. We shall adopt here the Lie symmetry approach to find symmetries of a given differential equation in both standard Newtonian- and the MONDian Gravity scenario and use them systematically to obtain group invariant solutions from invariant curve condition in context of cosmological perturbation theory. The interpretation sought by us has its origin in the classic work of Sophus Lie, who pioneered the modern approach for studying and finding special solutions of systems of nonlinear partial differential equations (PDEs) [27]. The method introduced by Lie ( 1891) considers the invariance of the form of the differential equation itself under set of point transformations of the dependent and independent variables. Recently there has been increasing interest in studying the symmetries of differential equations modeling physical systems. It has been applied, in recent years, to several equations of motion for dynamical systems.

More specifically, in this article, we shall derive the differential equations for density contrast in both Newtonian- and MONDian gravity laws using the linear density perturbation theory and find the solutions with a view to comparative study and investigate the physical features of the evolution of the growing- and decaying modes of density perturbations with respect to homogeneous isotropic cosmological background for both the cases. Here, we shall employ aforesaid time-honored Lie group theoretical approach to generate solutions for the density contrast equations in both standard Newtonian- and the MONDian Gravity scenario. The paper is organized as follows: Sect. 2 presents the derivation of the equations for the cosmological density perturbation in Newtonian and MONDian force laws. In Sect. 3 we shall present a general scheme for Lie symmetry analysis for second-order differential equation in order to use the results for the Lie theory to study the cosmological perturbation. We present the Lie symmetries for the equations governing the density fluctuation due to the gravity of Newtonian and MONDian force laws and then use these symmetries to find the exact analytical group invariant solutions for both the equations governing density fluctuation in Newtonian- and MONDian force laws in Sect. 4. We also checked the numerical solutions for the both cases. Finally, in Sect. 5, we shall discuss our analytical results with some concluding remarks.

2 Cosmological Density Perturbation

As we know that the measurements of the cosmic microwave background tell us that the universe was very homogeneous and isotropic at the time of recombination. Today, however, the universe has a well developed nonlinear structure. This structure takes the form of galaxies, clusters and superclusters of galaxies, and, on larger scales, of voids, sheets and filaments of galaxies. The simple explanation as to how nonlinear structures could develop from small initial perturbations is based on the fact of gravitational instability. The very first theory of structure formation was proposed by Sir. Jeans [3, 4] in context of a spherical Nebula. He supposed the universe to be filled with a non-relativistic fluid with mass density \(\rho \), pressure P and gravitational field g, governed by the equation of continuity, the Euler equation and the gravitational field equation [28]. What Jeans demonstrated was that density inhomogeneities grow in time when the pressure support is weak compared to the gravitational pull in a non expanding background. Jeans’s formula gives the condition that a gravitating mass of gas will be stable to small fluctuation in the density. Unfortunately, Jeans theory is not applicable to the formation of galaxies in an expanding universe because it was originally obtained for static mass of uniform density. Small perturbations of the average density die out and as a consequence Jeans’ formula cannot be applied in steady state theory for the formation of the nebulae, requires further substantiation [29]. The first satisfactory theory of instabilities of an expanding universe was given in 1946 by Lifshitz [5]. In this context, Bonnor [29] employed an expanding Newtonian world-model to study perturbations in a dust dominated FRW cosmology.

The cosmological theory of the expanding universe is at present generally accepted. To a high degree of accuracy the large scale features of the universe can be described by a homogeneous and isotropic cosmology, a Friedman-Lemaître–Robertson–Walker (FLRW) space time [6]. It becomes clear that the Newtonian analysis applies only to late times in the lifetime of our present flat universe when the universe is dominated by non-relativistic pressureless matter, which is commonly referred to as dust. In this context, Newtonian perturbation theory can be applied even with the presence of relativistic energy components, like radiation and dark energy, as long as they can be considered as smooth components and their perturbations can be ignored. Then they contribute only to the background solution. In this case we have to consider a dust dominated FLRW cosmology with flat spatial sections. This model, also known as the Einstein-de Sitter universe, is though to provide a good description of the universe after recombination, but the perturbation equations are the Newtonian perturbation equations. Star clusters, galaxies, galaxy clusters, superclusters and voids are evidence that on small and moderate scales, that is up to 10Mpc, our universe is very lumpy. As we move to larger and larger scales, however, the universe seems to smooth out. The Newtonian theory, as a limiting approximation of general relativity, is only applicable to scales well within the Hubble radius where the effects of space time curvature are negligible. The density contrast equation can also be derived from the pure Newtonian point of view by taking recourse to the use of the Newtonian fluid dynamical equations including a self-gravity term. For this we have to proceed with the equation of conservation of mass, the Euler equation, and the standard Poisson equation for the self-gravitational Newtonian potential \(\phi (\rho ,\,\vec {r})\) generated by a density field, \(\rho (\vec {r})\) and considering a small perturbation with respect to a homogeneous expanding background. The detailed derivation of the theory of cosmological density contrast have been studied using Newtonian equations of fluid dynamics taking into account the expansion of the universe in [28]. The line element for the homogeneous expanding universe can be written in spherical polar coordinates as

$$\begin{aligned} ds^2=-dt^2+a(t)^2\left[ \frac{dr^2}{(1-\kappa r^2)}+r^2(d\theta ^2+sin^2\theta d\phi ^2)\right] \,\,, \end{aligned}$$
(1)

where \(\kappa \) is the curvature index can have values \(+1,\,0,\,-1\), give three kinds of universe with positively curved, zero (flat) and negatively curved space respectively. a(t) is the scale factor. If we choose the universe is filled with a perfect fluid of radiation and nonrelativistic matter, characterized by their pressures p and energy densities \(\rho \) respectively, then the energy-momentum tensor for that perfect fluid can be written as [6]

$$\begin{aligned} T_{ij}=(\rho +p)u_iu_j+p g_{ij}\,\,, \end{aligned}$$
(2)

where \(\rho \) and p are the energy density and pressure respectively as measured in the rest frame, \(u_i\) is the four-velocity of the fluid and \(g_{ij}\) is the metric tensor. If a fluid which is isotropic in some frame leads to a metric which is isotropic in some other frame, then the two frames will coincide; that is, the fluid will be at rest in comoving coordinates. The four-velocity is then \(u_i=(1,\,0,\,0,\,0)\) and the energy momentum tensor is \(T_{ij}=diag(-\rho ,\,p,\,p,\,p)\). The energy-momentum tensor encapsulates all about the energy and momentum. The covariant derivative of \(T_{ij}\) gives the local law for the conservation of energy and momentum. This results

$$\begin{aligned} \dot{\rho }+3\frac{\dot{a}}{a}(\rho +p)=0\,\,. \end{aligned}$$
(3)

Here dot representing the time derivative. As all the perfect fluids relevant to cosmology obey the equation of state \(p=w\rho \), where w is constant independent of time, the equation for the energy conservation becomes

$$\begin{aligned} \frac{\dot{\rho }}{\rho }=-3(1+w)\frac{\dot{a}}{a}\,\,. \end{aligned}$$
(4)

This can be integrated to obtain

$$\begin{aligned} \rho \propto a^{-3(1+w)}\,\,. \end{aligned}$$
(5)

The two most popular examples of cosmological fluids are known as dust and radiation. Dust is collisionless, nonrelativistic matter, which obeys \(w = 0\). Examples include ordinary stars and galaxies, for which the pressure is negligible in comparison with the energy density. The energy density in matter falls off as \(\rho =\rho _{mat}\propto a^{-3}\). Whereas, the energy density in radiation falls off as \(\rho =\rho _{rad}\propto a^{-4}\), where \(w ={1\over 3}\). In this context, the energy density of the universe is dominated by matter, with \(\frac{\rho _{mat}}{\rho _{rad}}\sim 10^6\). However, in the past the universe was much smaller, and the energy density in radiation would have dominated at very early times. For the expanding flat (\(\kappa =0\)) FRW universe, taking recourse to the use of the General Relativity we can find the Friedmann equations

$$\begin{aligned} \left( \frac{\dot{a}}{a}\right) ^2=\frac{8\pi G}{3}\rho \end{aligned}$$
(6a)

and

$$\begin{aligned} \frac{\ddot{a}}{a}=-\frac{4\pi G}{3}(\rho +3p)\,\,, \end{aligned}$$
(6b)

from the Einstein equation [6]

$$\begin{aligned} R_{ij}-{1\over 2}g_{ij}R=8\pi G \,T_{ij}\,\,, \end{aligned}$$
(7)

where \(R_{ij}\) is the Ricci tensor and R the scalar curvature that measures the curvature of the space-time. In the right side of Eq. (7), \(T_{ij}\), the two-index energy-momentum tensor encompasses the energy density and pressure of the matter fields, which act as the source for gravity. For the expanding matter-dominated universe the transformation rule for the energy density for the matter can be written as

$$\begin{aligned} \frac{\rho }{\rho _{0}}=\left( \frac{a}{a_0}\right) ^{-3}\,\,. \end{aligned}$$
(8)

Here \(\rho _{0}\) is the value of the density for the moment when \(a = a_0\), which can be chosen as the present epoch. In the following subsection, we derive cosmological density perturbation for Newtonian- and MONDian cases.

2.1 Density Contrast Equation in Newtonian Case

In order to find the equation for the density perturbation, the basic tool we are following is first-order perturbation theory (also called linear perturbation theory). This means that we write all our inhomogeneous quantities as a sum of the background value, corresponds to the homogeneous and isotropic model, and a perturbation, that defines the deviation from the background value. By virtue of the Cosmological Principle the background FLRW Universe has a global uniform density. In context of galaxy formation, consider the universe is filled with a perfect fluid of non-relativistic matter characterized by their pressure p, energy density \(\rho \), velocity \(\vec {v}\). We also consider that the gravitational force is the only predominant external force acting on the fluid with gravitational field \(\vec {g}\). As the fluid is non-relativistic, from the perfect fluid conditions we can write the equation of continuity

$$\begin{aligned} \frac{\partial \rho }{\partial t}+ \vec {\nabla }\cdot (\rho \vec {v})=0\,\,, \end{aligned}$$
(9)

the Euler equation

$$\begin{aligned} \frac{\partial \vec {v}}{\partial t}+(\vec {v}\cdot \vec {\nabla })\vec {v}=-\frac{1}{\rho }\vec {\nabla }p+\vec {g} \end{aligned}$$
(10)

and the gravitational field equations

$$\begin{aligned} \vec {\nabla }\times \vec {g}= & {} 0\,\,, \end{aligned}$$
(11a)
$$\begin{aligned} \vec {\nabla }\cdot \vec {g}= & {} -4\pi G\rho \,\,. \end{aligned}$$
(11b)

It is easy to find the simple spatially uniform solutions of the above three equations that are valid when the quantities are not perturbed and the solutions are [6]

$$\begin{aligned} \rho= & {} \rho _0\left[ \frac{a_0}{a(t)}\right] ^3\,\,, \end{aligned}$$
(12a)
$$\begin{aligned} \vec {v}= & {} \vec {r}\left[ \frac{\dot{a}(t)}{a(t)}\right] \,\, \end{aligned}$$
(12b)

and

$$\begin{aligned} \vec {g}=-\vec {r}\left[ \frac{4\pi G\rho }{3}\right] \,\, \end{aligned}$$
(12c)

respectively. For the expanding universe, to find the perturbed equations, we consider a small perturbation \(\rho _1\), \(\vec {v_1}\) and \(\vec {g_1}\) which are added with the unperturbed value given in Eqs. (12). Using these perturbations on density, velocity and gravitational acceleration respectively in (9), (10), (11a) and (11b), we find the following perturbed equations

$$\begin{aligned}&\dot{\rho _1}+3\frac{\dot{a}}{a}\rho _1 +\frac{\dot{a}}{a}(\vec {r}\cdot \vec {\nabla })\rho _1 +\rho \vec {\nabla }\cdot \vec {v_1}=0\,\,, \end{aligned}$$
(13)
$$\begin{aligned}&\dot{\vec {v}}_1+\frac{\dot{a}}{a}\vec {v}_1 +\frac{\dot{a}}{a}(\vec {r}\cdot \vec {\nabla })\vec {v}_1 =-\frac{1}{\rho }\vec {\nabla }p_1+\vec {g_1}\,\,, \end{aligned}$$
(14)
$$\begin{aligned}&\vec {\nabla }\times \vec {g_1}=0\,\,, \end{aligned}$$
(15)
$$\begin{aligned}&\vec {\nabla }\cdot \vec {g_1}=-4\pi G\rho _1\,\,. \end{aligned}$$
(16)

The equations in (13)–(16) are spatially homogeneous and it is convenient to consider a plane wave solutions of these equations as in the following

$$\begin{aligned} \rho _1(r,t)= & {} \rho _1(t)e^{\left( \frac{i\vec {r}\cdot \vec {q}}{a(t)}\right) }\,\,, \end{aligned}$$
(17)
$$\begin{aligned} \vec {v}_1(\vec {r},t)= & {} \vec {v}_1(t)e^{\left( \frac{i\vec {r} \cdot \vec {q}}{a(t)}\right) }\,\,, \end{aligned}$$
(18)
$$\begin{aligned} \vec {g}_1(\vec {r},t)= & {} \vec {g}_1(t)e^{\left( \frac{i\vec {r} \cdot \vec {q}}{a(t)}\right) }\,\,. \end{aligned}$$
(19)

For expanding universe, the wavelength of the modes must be stretched out and therefore we have to multiply the scale factor a(t) with the wavelength to incorporate the expansion of the universe and that is why the term \(\frac{1}{a(t)}\) appears in the exponential term of the plane wave solutions. Also as we are considering the adiabatic fluctuations, we use a linear relationship between the pressure- and the density perturbation

$$\begin{aligned} p_1=v^2_s\rho _1\,\,, \end{aligned}$$
(20)

where \(v_s\) is the adiabatic speed of sound. Now using the plane wave solutions in (17) and (18) into Eqs. (13) and (14) we have

$$\begin{aligned}&\dot{\rho }_1+3\frac{\dot{a}}{a}\rho _1+i a^{-1}\rho \vec {q} \cdot \vec {v}_1=0\,\,, \end{aligned}$$
(21)
$$\begin{aligned}&\dot{\vec {v}}_1+\frac{\dot{a}}{a}\vec {v}_1=-\frac{i v^2_s}{\rho a}\vec {q} \rho _1+ \vec {g}_1=0\,\,. \end{aligned}$$
(22)

In writing Eq. (22) we have made use of Eq. (20). Here we can see that the Eqs. (21) and (22) are coupled. To solve these coupled equations of motion it is convenient to decompose \(\vec {v}_1\) into parts perpendicular (rotational) and parallel (irrotational) to \(\vec {q}\),

$$\begin{aligned} \vec {v}_1(t)=\vec {v}_{1\perp }+i\vec {q}\varepsilon (t)\,\,, \end{aligned}$$
(23)

where \(\vec {v}_{1\perp }\) is perpendicular to \(\vec {q}\) and \(\varepsilon \equiv -\frac{i\vec {q}.\vec {v_1}}{q^2}\). As we know that the \(\rho _1(t)\) accounts the change of the density from the unperturbed solution \(\rho (t)\), it is convenient to express the \(\rho _1(t)\) in terms of fractional density perturbation as follows

$$\begin{aligned} \rho _1(t)=\rho (t)\delta (t)\,\,. \end{aligned}$$
(24)

The fractional density perturbation \(\delta (t)\) can also be termed as density contrast. Taking recourse to the use of Eqs. (16), (19) and (23) in Eq. (22), it is easy to find the following two decoupled equations

$$\begin{aligned} \dot{\vec {v}}_{1\perp }+\frac{\dot{a}}{a}\vec {v}_{1\perp }=0\,\, \end{aligned}$$
(25)

and

$$\begin{aligned} \dot{\varepsilon }+\frac{\dot{a}}{a}\varepsilon =\left( -\frac{v^2_s}{a}+\frac{4\pi G\rho a}{q^2}\right) \delta \,\,. \end{aligned}$$
(26)

From (25) we can find that the rotational modes decay as \(a^{-1}\) and responsible for conservation of angular momentum and also these modes are not coupled to density perturbation. We are interested only for the irrotational modes i.e. Eq. (26) which is responsible for density perturbation. Now from (8) and (24) we find

$$\begin{aligned} \dot{\rho }_1(t)=-3\frac{\dot{a}}{a}\rho _1(t)+\rho (t)\dot{\delta }\,\,. \end{aligned}$$
(27)

On substitution of Eq. (27) into Eq. (21), we find

$$\begin{aligned} \dot{\delta }=\frac{q^2}{a}\varepsilon \,\,. \end{aligned}$$
(28)

Using (28) in (26) finally we get

$$\begin{aligned} \ddot{\delta }+2\frac{\dot{a}}{a}\dot{\delta }+\left( \frac{v^2_sq^2}{a^2}-4\pi G\rho \right) \delta =0\,\,. \end{aligned}$$
(29)

We can find the equation for the density difference compared to unperturbed density for matter dominated universe, where the matter pressure is negligible and there is no drag force between matter and radiation, by neglecting the pressure term in (29). This pressure term \(\frac{v^2_sq^2}{a^2}\) will be negligible compared with the gravitational term \(4\pi G\rho \) if the wave number \(|\vec {k}|\equiv \frac{|\vec {q}|}{a}\) is much less than the Jeans wave number [6]. From the above view points, the equation for cosmological density contrast for pressureless matter dominated universe, reduces to

$$\begin{aligned} \ddot{\delta } +2\frac{\dot{a}}{a}\dot{\delta }-4\pi G\rho \delta =0\,\,. \end{aligned}$$
(30)

If the universe is composed primarily of matter, then the big bang theory makes a definite prediction about the product of the expansion rate H of the universe, and the age t of the universe for matter-dominated flat universe, such that

$$\begin{aligned} H t={2\over 3}\,\,. \end{aligned}$$
(31)

Here H is the Hubble parameter and defined as \(\frac{\dot{ a}}{ a}\). The important conclusion of Eq. (31) is that the size (here the scale factor a) of the matter-dominated flat universe increases with time as \(t^{2\over 3}\). This solution for the non-relativistic matter-dominated flat universe is often called the Einstein-de Sitter model. Now taking recourse to the use of Eq. (31) for \(\ a\), we can write the Eq. (30) as

$$\begin{aligned} \ddot{\delta } +\frac{4}{3t}\dot{\delta }-\frac{2}{3t^2}\delta =0\,\,. \end{aligned}$$
(32)

Equation (32) describe the evolution of the cosmological density contrast derived in the limit of Newtonian approximation. Keeping only terms to first order in the perturbation, the resulting equations, for large scale regime where the pressure term is neglected, can be recast in the form [6, 7, 28]

$$\begin{aligned} \ddot{\delta } +2\frac{\dot{a}}{a}\dot{\delta }=\nabla ^2\delta \phi \,\,. \end{aligned}$$
(33)

In the following subsection we shall find the form of \(\nabla ^2\delta \phi \) in the MONDian case. In Newtonian case, we have \(\nabla ^2\delta \phi =4\pi G\rho \delta \).

2.2 Density Contrast Equation in MONDian Case

Milgrom [14] presented a new theory that accounts for the mass discrepancies in galactic systems without non-baryonic dark matter. Particularly, he developed a non-relativistic theory of gravity in order to explain observed flat rotation curves of spiral galaxies. In this context, it is also very important to note that few authors [30, 31] studied the dynamics of clusters of galaxies in the realm of the Modified Newtonian Dynamics (MOND) using X-ray data. They have shown the MOND hypothesis, as a stand alone solution, has proven to be unable to solve the missing mass problem at the clusters scale and investigated the hypothesis of massive neutrinos distributed as a sphere of constant density up to half the virial radius of galaxy clusters. Although MOND has some discrepancy in explaining the dynamics of clusters of galaxies, this theory has proved useful in explaining a great variety of astronomical phenomena without requiring the presence of a dark matter component. In particular, Milgrom [32] proposed a novel paradigm which can be interpreted as reflecting non-Newtonian as well as nonlinear character of gravity already at the non-relativistic level. In MOND theory he introduced the relation between the acceleration \(\vec {a}_c\) of a particle and the ambient conventional Newtonian gravitational field \(-\vec {\nabla }\phi \) by assuming an interpolation function \(\mu (y)\), \(\mu (y)\vec {a}_c=-\vec {\nabla }\phi \), where \(y=\frac{|\vec {a}_c|}{a_{c0}}\). If the function \(\mu =1\), this would be usual Newtonian dynamics. Milgrom [32] assumes that the positive smooth monotonic function \(\mu \) approximately equals its argument y when this is small compared to unity (deep MOND limit), but tends to unity when y is large compared to unity. In other words, the new constant \(a_{c0}\), with the dimensions of acceleration, marks the borderline between the Newtonian/MONDian physics valid approximately for accelerations (\(a_c\)) much larger/smaller than \(a_{c0}\) respectively. The quantity \(\vec {\nabla }\delta \phi \) depends on the theory of gravity one assumes. In this context, for circular motion of a test particle at a distance R around a point mass M. On dimensional grounds alone, the expression for MOND acceleration of the particle must be of the form \(\frac{MG}{R^2}\mu \left( \frac{MG}{R^2a_{c0}}\right) \). The MOND basic tenets require that for \(\frac{MG}{R^2}>>a_{c0}\) we have \(\mu \rightarrow 1\), while for \(\frac{MG}{R^2}<<a_{c0}\) we have to have scale invariance, which dictates \(\mu (y)\approx y^{-{1\over 2}}\) and effectively \(\vec {\nabla }\phi \approx \frac{\sqrt{ {a_{c0}GM}}}{R}\), which are relevant to more general systems: for a given mass, M, the asymptotic acceleration at large radii goes as \(R^{-1}\) compared with the standard \(R^{-2}\) [32]. Following [32], for the system, we can write the MONDian potential \(\vec {\nabla }\delta \phi =\frac{\sqrt{ {a_c}_0G\delta m}}{r}\) and use safely the acceleration below \({a_{c0}}=1.2\times 10^{-8}\,cm/s^2\) limit of the extended gravity force law when working in the linear regime where the density contrast is small. Also this value is tantalizingly close to acceleration parameters that characterize cosmology [14, 32] and for another support, Nusser [25] use N-body simulations to solve the MOND equations of motion, starting from initial conditions with a cold dark matter (CDM) power spectrum and shown that MOND with the standard value \(a_{c0}=1.2\times 10^{-8} cm/s^2\) yields a high clustering amplitude that can match the observed galaxy distribution only with strong (anti-) biasing. For a top-hat density fluctuation, \(\delta m={4\over 3}\pi r^3\delta _{\rho _m}\), where \(\delta m\) represents the mass fluctuation, we can write

$$\begin{aligned} \vec {\nabla }\delta \phi =\left( \frac{4 \pi }{3}{a_c}_0Gr\delta _{\rho _m}\right) ^{1\over 2} \end{aligned}$$
(34)

and consequently we obtain the Laplacian of the MONDian potential (using radial component)

$$\begin{aligned} \nabla ^2\delta \phi =\left( \frac{25 \pi }{3r}{a_c}_0G\delta _{\rho _m}\right) ^{1\over 2}=\frac{5}{2}\left( \frac{4 \pi \rho _m}{3}\right) ^{2\over 3}\frac{(G{a_c}_0)^{1\over 2}}{(\delta m)^{1\over 6}}\delta ^{2\over 3}\,\,. \end{aligned}$$
(35)

To write Eq. (35) we have used \(\delta _{\rho _m}=\rho _m\delta \). Eq. (33), in an extended MONDian scenario, reduces to the following form

$$\begin{aligned} \ddot{\delta } +2\frac{\dot{a}}{a}\dot{\delta }=\frac{5}{2}\left( \frac{4 \pi {\rho }_m}{3}\right) ^{2\over 3}\frac{(G{a_c}_0)^{1\over 2}}{(\delta m)^{1\over 6}}\delta ^{2\over 3}\,\,. \end{aligned}$$
(36)

Using the value of \(a=a_0(3H_0t/2)^{2/3}\) for the matter-dominated expanding universe and considering only the baryonic matter density \(\rho _m=0.05\rho _{m0}\left( \frac{a_0}{a}\right) ^3=0.05\rho _{m0}(1+z)^3\), where z is redshifts and \(\rho _{m0}=\frac{3H_0^2}{8\pi G}\), we find (36) in the following form

$$\begin{aligned} \ddot{\delta } +\frac{4}{3t}\dot{\delta }-c\frac{\delta ^{2\over 3}}{t^{4\over 3}}=0\,\,, \end{aligned}$$
(37)

where \(c=0.124\frac{({a_c}_0)^{1\over 2}}{(G\delta m)^{1\over 6}}\). In the next section we shall present a general scheme for Lie symmetry analysis and group invariant solution for the second-order differential equation.

3 Lie Symmetry and Group Invariant Solution

A second-order ordinary differential equation of the form \(M(t,\,x,\,\dot{x},\,\ddot{x})=0\) possesses Lie point symmetries of the form

$$\begin{aligned} X=\xi (x,\,t)\frac{\partial }{\partial t}+\eta ( x,\,t)\frac{\partial }{\partial x}\,\, \end{aligned}$$
(38)

provided [27]

$$\begin{aligned} X^{(2)}M(t,\,x,\,\dot{x},\,\ddot{x})=0\,\,, \end{aligned}$$
(39)

where \(X^{(2)}\) is the second-order prolongation of the vector field X obtained by specializing (38) to \((1+1)\) degrees of freedom. The prolonged infinitesimal generator of order m corresponding to X in Eq. (38) is written as [27]

$$\begin{aligned} X^{(m)}=X+X_1+X_2+...+X_m\,\,, \end{aligned}$$
(40)

with

$$\begin{aligned} X^{(1)}=X+X_1=X+\left[ \dot{\eta }(x,t)- \dot{\xi }(x,t)\dot{x}\right] \frac{\partial }{\partial \dot{x}}\,\, \end{aligned}$$
(41a)

and

$$\begin{aligned} X^{(2)}=X+X_1+X_2=X^{(1)}+\eta ^{''}\frac{\partial }{\partial \ddot{x}}\,\, \end{aligned}$$
(41b)

and so on. In writing (41b) we used

$$\begin{aligned} \eta {''}=\left[ \ddot{\eta }(x,t)-2\dot{\xi }(x,t)\ddot{x}- \ddot{\xi }(x,t)\dot{x}\right] \,\,. \end{aligned}$$
(41c)

Here it is to be noted that the functions \(\xi (x,t)\) and \(\eta (x,t)\) are not infinitesimals. These are the coefficient functions of a finite differential operator which, when coupled with infinitesimal parameter, gives the generator of the infinitesimal transformation. Now we shall use Eq. (39) to find the Lie symmetries for the Eqs. (32) and (37).

Group invariant solution To find the group invariant solution generated by the particular generator X, let us consider any curve C. It is an invariant curve if and only if the tangent to C at each point (t, x) is parallel to the tangent vector \((\xi (t,\,x),\,\, \eta (t,\,x))\). This condition can be expressed mathematically by introducing the characteristic \(Q=\eta (t,\,x)-\dot{x}\xi (t,\,x)\). Every curve C on the (t, x) plane that is invariant under the group generated by X satisfies

$$\begin{aligned} Q\equiv \eta (t,x)-\dot{x}\xi (t,x)=0 \end{aligned}$$
(42)

on C. We can find the invariant solutions generated by the above symmetry generators using the invariant curve condition (42). In the following section, we shall study the Lie symmetries and the solutions of Eqs. (32) and (37).

4 Lie Symmetries and Group Invariant Solutions for Eqs. (32) and (37)

4.1 Lie Symmetries for Eq. (32)

From Eq. (32) we can write

$$\begin{aligned} M(t,\,x,\,\dot{x},\,\ddot{x})=\ddot{x} +\frac{4}{3t}\dot{x}-\frac{2}{3t^2}x\,\,. \end{aligned}$$
(43)

Now making use of Eqs. (39), (41), and applying the second extension on (43) we get

$$\begin{aligned}&\left( \xi _{tt}-2\eta _{xt}-\frac{4}{3t}\xi _t+\frac{2 x}{t^2}\xi _x+\frac{4}{3t^2}\xi \right) \nonumber \\&\quad +\left( -\eta _{tt}+\frac{4x}{3t^2}\xi _t-\frac{4}{3t}\eta _t-\frac{2 x}{3t^2}\eta _x-\frac{4 x}{3t^3}\xi +\frac{2}{3t^2}\eta \right) \dot{x}\nonumber \\&\quad +\left( 2\xi _{xt}-\eta _{xx}-\frac{8}{3t}\xi _x\right) {\dot{x}}^2-\xi _{xx}{\dot{x}}^3=0\,\,. \end{aligned}$$
(44)

Equation (44) can be globally satisfied for any particular choice of \(\dot{x}\) provided the sum of \(\dot{x}\) independent terms, the coefficients of linear, quadratic and cubic terms in \(\dot{x}\) vanish separately. This viewpoint leads to four determining equations for infinitesimal generators \(\xi \) and \(\eta \). In particular we have

$$\begin{aligned}&{\dot{x}}^3\,\,:\,\,\,\xi _{xx}=0\,\,, \end{aligned}$$
(45a)
$$\begin{aligned}&{\dot{x}}^2\,\,:\,\,\,2\xi _{xt}-\eta _{xx}-\frac{8}{3t}\xi _x=0\,\,, \end{aligned}$$
(45b)
$$\begin{aligned}&{\dot{x}}\,\,:\,\,\,-\eta _{tt}+\frac{4x}{3t^2}\xi _t -\frac{4}{3t}\eta _t-\frac{2 x}{3t^2}\eta _x-\frac{4 x}{3t^3}\xi +\frac{2}{3t^2}\eta =0 \end{aligned}$$
(45c)

and

$$\begin{aligned} {\dot{x}}^0\,\,:\,\,\,\xi _{tt}-2\eta _{xt}-\frac{4}{3t}\xi _t+\frac{2 x}{t^2}\xi _x+\frac{4}{3t^2}\xi =0\,\,. \end{aligned}$$
(45d)

Solving Eqs. (45a)–(45d) we find

$$\begin{aligned} \xi (t,x)=c_1t+c_4t+3 c_5t^2 x-\frac{c_6}{t^{2\over 3}}+3c_7t^{8\over 3}+c_8t^{1\over 3}x \end{aligned}$$
(46a)

and

$$\begin{aligned} \eta (t,x)=\frac{c_2}{t}+c_3t^{2\over 3}+4c_4 x+2c_5tx^2+\frac{c_6x}{t^{5\over 3}}+2c_7xt^{5\over 3}-\frac{c_8x^2}{t^{2\over 3}}\,\,. \end{aligned}$$
(46b)

Here \(c_i\), \(i=1,\,2,\,3,....\) are the arbitrary constants and consequently, we have the following eight Lie-point symmetries

$$\begin{aligned} X_1= & {} t\partial _t\,\,, \end{aligned}$$
(47a)
$$\begin{aligned} X_2= & {} t\partial _x\,\,, \end{aligned}$$
(47b)
$$\begin{aligned} X_3= & {} t^{2\over 3}\partial _x\,\,, \end{aligned}$$
(47c)
$$\begin{aligned} X_4= & {} t\partial _t+4x\partial _x\,\,, \end{aligned}$$
(47d)
$$\begin{aligned} X_5= & {} 3t^2 x\partial _t + 2tx^2\partial _x\,\,, \end{aligned}$$
(47e)
$$\begin{aligned} X_6= & {} -t^{-{2\over 3}}\partial _t+xt^{-{5\over 3}}\partial _x\,\,, \end{aligned}$$
(47f)
$$\begin{aligned} X_7= & {} 3t^{8\over 3}\partial _t+2xt^{5\over 3}\partial _x \end{aligned}$$
(47g)

and

$$\begin{aligned} X_8=t^{1\over 3}x\partial _t-x^2t^{-{2\over 3}}\partial _t\,\,. \end{aligned}$$
(47h)

Solution for Eq. (32) For the symmetry generator \(X_5\) and \(X_7\) using invariant curve condition given in Eq. (42), identifying \(\delta \) as x, we find the solution of Eq. (32) is \(\delta \sim t^{2\over 3}\) and for the symmetry generators \(X_6\) and \(X_8\) the solution is of the form \(\sim t^{-1}\). The general solution of the Eq. (32) for matter-dominated universe

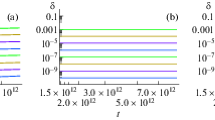
$$\begin{aligned} \delta =c_1 t^{2\over 3}+c_2 t^{-1} \end{aligned}$$
(48)

for the evolution of the density contrast. There are two solutions: one growing and one decaying. Any given perturbation is expressed as a linear combination of the two modes. At late times, however, only the growing mode is important. The first solution involves a growth of the densities in the universe. It is an important point to note that in the specific case of an Einstein-de Sitter universe, the growth is proportional to the scale factor of the universe. Hence we find that in this situation, perturbations grow due to the effect of gravity; the growing solution, is normally called the growing mode. The second solution, on the other hand, leads to a continuously declining density contrast: the primordial density contrast is diminishing in time, known as decaying mode solution. From Eqs. (8), (24) and (48) we find that the density perturbation \(\rho _1=\rho (t) \delta (t)\propto t^{-{4\over 3}}\) for the growing mode solution whereas for decaying mode solution \(\rho _1=\rho (t) \delta (t)\propto t^{-3}\). Thus perturbed density for decaying mode solution decays faster than that of the growing mode solution. In Fig. 1 we have shown the evolution of the density contrast solved numerically from Eq. (32) for the period from the recombination era to present age of the universe. Particularly, we have taken different values of the initial amplitudes of the density contrast \(\delta =10^{-9.5},10^{-9},10^{-8},10^{-7},10^{-6},10^{-5}\) and \(\frac{d\delta }{dt}=0\) as initial conditions at the initial time, here recombination era. From Fig. 1, it is clear that the evolutionary tracks of the density contrast \(\delta \) for different initial conditions remain parallel throughout for the Newtonian case. We can see small deeps in the density contrast in Fig. 1 near the recombination time because during this period the decaying mode solution is dominating over the growing mode and after that the growth solution sustains which is responsible for the structure formation.

Fig. 1
figure 1

(Color online) Figure shows the variation of density contrast using Eq. (32) solved numerically for the initial conditions \(\delta =10^{-9.5},10^{-9},10^{-8},10^{-7},10^{-6},10^{-5}\) and \(\frac{d\delta }{dt}=0\) at the time of recombination era (the initial time)

Full size image

4.2 Lie Symmetries for Eq. (37)

From Eq. (37) we can write

$$\begin{aligned} M(t,\,x,\,\dot{x},\,\ddot{x})=\ddot{x} +\frac{4}{3t}\dot{x}-c\frac{x^{2\over 3}}{t^{4\over 3}}\,\,. \end{aligned}$$
(49)

By performing the similar analysis for (49) as given in the previous Sect. 4.1 for finding the Lie symmetry, we find only one symmetry for Eq. (37) given by

$$\begin{aligned} X=t\partial _t+2x\partial _x\,\,. \end{aligned}$$
(50)

Now we shall make use of the symmetry in (50) to find the group invariant solution of Eq. (37) to realize the nature of the time evolution of the density contrast for the MONDian gravity.

Solution for Eq. (37) Similarly, making use of (42) and (50) we obtain the group invariant solution for Eq. (37) of the form

$$\begin{aligned} \delta =c_3 t^2. \end{aligned}$$
(51)

This represents the evolution of the density contrast for modified extended gravity scenario provided the constant \(c_3\) in (51) satisfies the relation \(c_3=({3c\over 14})^3\) with c given in (37). Now using \(t^2=\frac{4 a^3}{9H_0^2a_0^3}\) in (51) we find the expression for the density contrast as

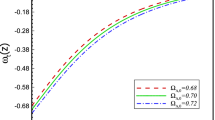
$$\begin{aligned} \delta= & {} 8.338\times 10^{-6}\left( \frac{a_{c0}^{3\over 2}}{G^{1\over 2}H_0^2\delta m^{1\over 2}}\right) (1+z)^{-3}\nonumber \\= & {} 2.604\times 10^{20}(1+z)^{-3}\delta m^{-{1\over 2}}\,\,. \end{aligned}$$
(52)

In writing Eq. (52) we have used the standard values for \(a_{c0}=1.2\times 10^{-10}\,ms^{-2}\), \(G=6.67\times 10^{-11}\,m^3kg^{-1}s^{-2}\) and \(H_0=70\, kms^{-1}Mpc^{-1}\). It is clear from (52) that \(\delta \sim \frac{1}{\delta m^{1\over 2}}\). From Eq. (52), we can estimate the mass fluctuation \(\delta m\) arises from the density fluctuation theory in MONDian gravity law for particular density contrast value and redshift. As we know the growth of density contrast is proportional to the scale factor of the universe for Newtonian case. Contrary to Newtonian case, Eq. (51) shows that the growth in density contrast is cubic order to the scale factor if we used the MONDian force law. This enhanced order of proportionality for the MONDian case results in a more rapid structure formation than for the Newtonian case. Results for the evolution of growth factor from Eq. (52) are shown in Fig. 2 from the time of recombination \((\frac{a}{a_0}=\frac{1}{1001})\) to the present age \((\frac{a}{a_0}=1)\), for different values of \(\delta m=2.158\times 10^{35},\,10^{36},\,10^{37},\,10^{38},\,10^{39},\,10^{40}Kg\) that appears in descending order. The lower limit for the value of initial fluctuation mass is chosen as the baryonic MONDian Jeans mass \(\delta m=\frac{\sigma ^4}{Ga_{c0}}=2.158\times 10^{35}Kg\) at time of recombination with \(\sigma \) the speed of sound at 3000 K hydrogen gas. It is clear from Eqs. (51) and (52) that the density contrast shows not only a definitive power law behavior but also furnishes a unique amplitude fully determined by the physical parameter \(H_0\), \(a_{c0}\) and G at all redshifts, once a mass fluctuation is chosen. The solution (51) or (52) of Eq. (37) is a strongly attractive solution. We can analyze this from Eq. (37). The source term \(\delta \) in the right hand side of Eq. (37) appears to a power smaller than 1. If we take an enhanced solution having a slightly larger amplitude at a given reference redshift than a given reference solution in (52), the source term will proportionally be smaller than the increase in \(\delta \) itself and the reference solution will catch up with enhanced variant. This is shown explicitly in Fig. 3, where the numerical solutions of Eq. (37) are shown for constant fluctuation mass of \(10^6\)\(M_\odot \), for a range of time from recombination \((\frac{a}{a_0}=\frac{1}{1001})\) to the present age \((\frac{a}{a_0}=1)\) all with \(\frac{d\delta }{dt}=0\) at initial time. Interestingly we also see all the numerical solutions converge to the symmetry-based solution (51) or (52) shown by arrow in Fig. 3 for the same fluctuation mass. This is a clear indication for a stable attractive solution. Thus resulting structure formation scenario is highly independent of the initial value of the density contrast and the evolution is purely determined by the fluctuation mass.

Fig. 2
figure 2

(Color online) Plot shows a set of growth of density contrasts using the symmetry-based solution (52) of Eq. (37) for different values of \(\delta m=2.158\times (10^{35},10^{36},10^{37},10^{38},10^{39},10^{40})Kg\) that appears in descending order

Full size image
Fig. 3
figure 3

(Color online) Plot shows the numerical solution of Eq. (37) for the constant fluctuation mass \(10^6\)\(M_\odot \). Notice the strong convergence to the symmetry based solution in (52) for the same fluctuation mass (shown by arrow)

Full size image

5 Conclusion

In conclusion, we derive the evolution equation for linear density perturbations governed by Newtonian and MONDian force laws, where the perturbation is taken with respect to a homogeneous Friedmann-Robertson-Walker (FRW) background in non-relativistic pressureless matter-dominated flat universe. This is applicable to scales well within the Hubble radius where the effect of space time curvature are negligible. The same second-order differential equation for the density contrast \(\delta \), can also be derived from the equation of conservation of mass, the Euler equation, and the standard Poisson equation for the self-gravitational Newtonian potential \(\phi (\rho ,\,\vec {r})\) generated by a density field, \(\rho (\vec {r})\) by considering a small perturbation with respect to a homogeneous expanding background from the Newtonian point of view [6, 28]. We use Lie symmetry approach to study the evolution of the density contrast in matter dominated universe. Particularly, we find eight-parameter Lie group symmetries for the linear order density perturbation equation and use Lie symmetries to find the group invariant solutions from invariant curve condition. The solution (Eq. (48)) found from Lie symmetry exactly matches with the growing as well as decaying mode solutions of density contrast in existing literature [6, 7]. The first term is the growing mode and the second term the decaying mode. After some time the decaying mode has died out, and the perturbation grows as \(\delta \propto t^{2\over 3}\propto a\), the scale factor. The exact nature of decaying and growing mode solutions are shown numerically in Fig. 1. The evolutionary tracks of the density contrast \(\delta \) for different initial conditions remain parallel throughout for the Newtonian case. We can also see small deeps in the density contrast in Fig. 1 near the recombination time because during this period the decaying mode solution is dominating over the growing mode and after that the growth solution sustains which is responsible for the structure formation. This growth of perturbations in an expanding universe is a consequence of gravitational instability and the perturbation grows at the same rate as the scale factor of the Einstein-de Sitter universe filled with non-relativistic pressureless matter. The instability of primordial density fluctuations as observed in the CMB, to grow into the present day astronomical structures is well established under Newtonian and Einstein gravity. But the actual amplitude of the density fluctuation is much larger than what the CMB observations imply for the baryons. Therefore, we have studied the equation for density fluctuation through MONDian force law and solved the system using Lie symmetric approach. From symmetric solution (Eqs. (51) and (52)), we can see that the perturbation grows as \(\delta \propto t^2\propto a^3\). It is an interesting conclusion that the growth factor for the case of MONDian force law is of 9 orders of magnitude, rather than the 3 orders of the Newtonian case. A small overdensity will exert an extra gravitational attractive force on the surrounding matter. Consequently, the perturbation will increase and will in turn produce a larger attractive force that we have shown for the case of MONDian force law through the numerical analysis of Eqs. (36) or (37) in Fig. 3. It is also interesting to note that all the numerical solutions converge to the symmetry-based attractive solution (51).

The primordial density fluctuations should have left their imprint on the cosmic microwave background radiation in the form of small variations in the temperature of this radiation in different directions on the sky. Both gravity waves as well as adiabatic density perturbations arise as natural consequences of the inflationary scenario, due to the superadiabatic amplification of zero-point quantum fluctuations occurring during inflation. The universe has expanded by a factor of \(10^3\) since decoupling, and so at that epoch, we require the initial size of the density perturbation should satisfy \(\delta >10^{-3}\). However, the temperature fluctuations in the microwave background that corresponds the density perturbations were only of the order of \(\frac{\Delta T}{T}\approx \delta \approx 10^{-5}\) at the time of decoupling and this is too small by some two orders of magnitude. In other words, in a universe containing just baryonic matter under Newtonian force law would not have been sufficient time from decoupling through to the present era for structures such as galaxies to form by gravitational attraction. In our study we have given an account for the density contrast, as well as mass fluctuation by solving both Newtonian and the MONDian density perturbation theory in context of cosmological structure formation through Lie symmetry approach. We have seen that the MONDian force law generates higher amplitudes in the density fluctuation that cannot be possible for the Newtonian force law. We also hope that the CMB and Large-scale structure experiments in coming years will bring definitive constraints on \(m_\nu \) in the astrophysical context, and should definitively settle the case of the MOND paradigm [17,18,19, 30, 31]. Finally, till there remains some questions. Is it possible to construct a MOND universe which can reproduce current observations of the CMB and galaxy surveys? As we also have discussed in introduction that the dynamics of clusters and Bullet cluster tell us that MOND still requires a small fraction of non-baryonic dark matter. Thus the answer may come out from further analysis of large scale structure fromation in the framework of Bekensteins Theory of Relativistic Modified Newtonian Dynamics in which the MOND is in the weak-field nonrelativistic limit [12] and/or we have to search for true connections between MOND and cosmology [23].