The Invisibility of Diffeomorphisms

Abstract

I examine the relationship between $(d+1)$-dimensional Poincaré metrics and d-dimensional conformal manifolds, from both mathematical and physical perspectives. The results have a bearing on several conceptual issues relating to asymptotic symmetries in general relativity and in gauge–gravity duality, as follows: (1: Ambient Construction)  I draw from the remarkable work by Fefferman and Graham (Elie Cartan et les Mathématiques d’aujourd’hui, Astérisque, 1985; The Ambient Metric. Annals of Mathematics Studies, Princeton University Press, Princeton, 2012) on conformal geometry, in order to prove two propositions and a theorem that characterise which classes of diffeomorphisms qualify as gravity-invisible. I define natural notions of gravity-invisibility (strong, weak, and simpliciter) that apply to the diffeomorphisms of Poincaré metrics in any dimension. (2: Dualities) I apply the notions of invisibility, developed in (1), to gauge–gravity dualities: which, roughly, relate Poincaré metrics in $d+1$ dimensions to QFTs in d dimensions. I contrast QFT-visible versus QFT-invisible diffeomorphisms: those gravity diffeomorphisms that can, respectively cannot, be seen from the QFT. The QFT-invisible diffeomorphisms are the ones which are relevant to the hole argument in Einstein spaces. The results on dualities are surprising, because the class of QFT-visible diffeomorphisms is larger than expected, and the class of QFT-invisible ones is smaller than expected, or usually believed, i.e. larger than the PBH diffeomorphisms in Imbimbo et al. (Class Quantum Gravity 17(5):1129, 2000, Eq. 2.6). I also give a general derivation of the asymptotic conformal Killing equation, which has not appeared in the literature before.

1 Introduction

The asymptotic symmetries of gravity have been a central foundational topic in general relativity since at least the work Arnowitt et al. [3, 4], Sachs [34, 35], Bondi et al. [7], Penrose [32, 33], Newman et al. [31], Geroch [20], Ashtekar et al. [5], and others. A central question is whether there are asymptotic diffeomorphisms that act on the physical degrees of freedom of the gravity theory, and how these diffeomorphisms are to be characterised. Only very recently has it for example been realized that, for Schwarzschild spacetimes, there are—in addition to the usual ADM mass, momentum, and angular momentum—an infinite number of conserved supertranslation and superrotation charges, which act non-trivially on the physical phase space [23].

In this paper, I analyse the case of a negative cosmological constant. (For a discussion of the other cases: see the physical motivation, below.) I will use gauge–gravity duality to argue that there is a significant, non-empty, class of diffeomorphisms—which I will, broadly speaking, call ‘visible’, in a sense that I will make precise—which act on the dual gauge theory, and which act on the physical degrees of freedom of the gravity theory. And there is a class of ‘invisible’ diffeomorphisms which do not act on the asymptotic quantities. The latter class invites a comparison with Einstein’s hole argument.

I will develop techniques to characterise these two classes, and I will prove a theorem and two propositions about them.

Diffeomorphisms and Gauge–Gravity Duality Gauge–gravity dualities are surprising relationships between gravity theories, typically defined in $d+1$ dimensions, and quantum field theories (QFTs) in d dimensions. The duality is usually construed as an ‘isomorphism’ between all the physical quantities on either side. One important question for dualities is what part of the content of the theory is ‘physical’, and thus mapped by the duality: and what part of content is ‘unphysical’, specific to one of the two sides, hence not mapped by the duality—it will be invisible to duality. Gauge symmetries in QFT are of this kind: if the QFT has a gauge symmetry, its physical quantities are gauge invariant and are treated as such by the duality—the gauge symmetry is not seen on the dual side.

One naturally expects that the diffeomorphism invariance of the gravity theory is also of this kind: what is physical in a gravity theory should be independent of the coordinates chosen, and so one would naively not expect the duality to ‘see’ the action of diffeomorphisms in the gravity theory. The QFT does not possess diffeomorphism invariance, and so the diffeomorphisms should be invisible to it. But there is one well-known class of diffeomorphisms that is visible through the duality map and which thereby can acquire a physical meaning [12, Sect. 1.3.2]. Namely, the QFT is invariant under the coordinate transformations that leave its background geometry fixed. In the cases where the QFT has an UV fixed point (at which it is a conformal field theory, or CFT), the conformal group is known to arise, through the duality map, from a restricted class of diffeomorphisms of the gravity theory, which go under the name of PBH transformations (Brown and Henneaux [8, Sects. III–IV]) [13, 26].

The difference between the two kinds of diffeomorphisms—those that are visible versus those that are invisible through the duality—is thus a crucial property of the duality map, and determines what is ‘physical’, on both sides of the duality. The diffeomorphisms differ both in their physical properties and in the ways in which they can be regarded to be novel properties of the gravity theory. While I will leave the question of emergence of diffeomorphisms for the future¹: in this paper I will focus on the mathematical and physical contrast between visible and invisible diffeomorphisms.

Physical Motivation and Generality of the Results Let me describe in more detail the two main physical motivations for this work: namely, from general relativity, and from quantum gravity.

As for classical general relativity: there is, of course, a large and venerable literature on boundary conditions, and diffeomorphisms which preserve them, in general relativity: especially in the asymptotically flat case. Arnowitt et al. [3, 4] developed the definition of energy using the ADM formalism, in which spacetime is foliated into a family of spacelike surfaces, and they parametrised the four-dimensional metric in terms of a three-dimensional metric on the surface and four functions, the lapse function and the shift vector. Sachs [34, 35] and Bondi et al. [7] studied in detail the question of asymptotic symmetries at null infinity in asymptotically flat spacetimes, a problem that is highly relevant to e.g. gravitational waves. The asymptotic symmetry group discovered now goes under the name of the BMS group. This led to other important results, such as Penrose’s [32, 33] treatment of conformal infinity, which also holds in the presence of a non-zero cosmological constant. The asymptotically flat case was further developed in works such as Newman et al. [31], Geroch [20], Ashtekar et al. [5], and others.

The case of a negative cosmological constant has been treated, with a variety of motivations, in the works cited in the preamble of this Introduction. Other important work is e.g. Ishibashi et al. [27], which focuses on AdS’s lack of global hyperbolicity.

The case of a positive cosmological constant is the poorest understood. Relevant works are e.g. Anninos et al. [2] and Ashtekar et al. [6], and references therein.

While the cosmological constant in our universe is of course not negative² (nor is it zero!), there are several motivations, from classical general relativity, for taking up the case of a negative cosmological constant once again: in addition to the ones already mentioned earlier.

First of all, as in Ishibashi et al. [27], the case of negative cosmological constant is non-globally hyperbolic (since pure AdS is “like a box”), and so understanding in detail how to define boundary conditions, and how boundary conditions and diffeomorphisms mesh, is quite relevat for the treatment of solutions more generally in open regions of the universe, where observers within any finite region have no access to infinity within a finite time. And so, it is of conceptual and practical importance to understand general relativity for open systems (the Schwarzschild black hole being a related example).

Second, the techniques which I develop in this paper can be generalised, by an analytic continuation $\ell _\mathrm{{AdS}}\mapsto i\,\ell _\mathrm{{dS}}$, to the cosmologically relevant case of a positive cosmological constant: as I discuss towards the end of Sect. 4 (for details on how this map acts, see De Haro et al. [15, Sect. 8]). The analytic continuation maps the timelike boundary to a spacelike boundary. In fact, one expects not only the mathematical techniques, but also some of the conceptual lessons, to carry over to that case: such as the bulk/hole argument of De Haro et al. [14, Sect. 6], and the notion of gravity-invisible diffeomorphisms.

But there is of course also, in addition to these classical considerations, a quantum gravity motivation: understanding the classical structure of gauge–gravity duality is an important step towards understanding the duality at the quantum level. For asymptotic symmetry structures are of course important for the quantisation of gravity. Since candidate quantum gravity theories do not abound, developing AdS/CFT is a worthwhile exercise. And as stressed in De Haro [12]: the content that is invariant across the duality (the ‘common core’) is what should be regarded as physically significant for this particular theory of quantum gravity. This gives us an additional argument to the effect that the diffeomorphisms which are visible to the QFT also act on general relativity’s asymptotic degrees of freedom.

The question, of which class of diffeomorphisms are physical and which are unphysical, is an important question for dualities in general—as it is for gauge theories. It also bears on the definition of observables, background-independence, and emergence. Thus AdS/CFT is a good case study which has already provided insights into possibilities for defining a gauge–gravity duality for spaces with a positive cosmological constant (see e.g. Maldacena [29], Strominger [38], De Haro et al. [15, Sect. 8]).

1.1 Conformal Geometry and Summary of the Results

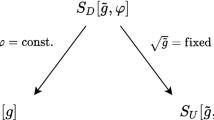
I will draw on the so-called ambient construction in conformal geometry—a remarkable piece of mathematics by Fefferman and Graham [18, 19]—in order to prove two propositions and a theorem which apply to general relativity and gauge–gravity dualities. The mathematical results concern the conditions under which a diffeomorphism, in a gravity theory with a gauge dual, is ‘invisible’ to the gauge theory.³ I will provide four notions of invisibility, three concerning the gravity theory and one concerning the gauge theory. The notions of gravity-invisibility amount to a diffeomorphism being invisible if it fixes certain mathematical structures in the gravity theory:

• (i) the form of the metric: i.e. a class of Poincaré metrics,

• (ii) the conformal manifold at the boundary: in terms of its points, or

• (iii) the representative of the conformal class of metrics with which the boundary manifold is equipped.

As we will see in Sect. 2, fixing (ii) does not imply fixing (iii): for the class of diffeomorphisms fixing (ii) include non-trivial conformal transformations at the boundary, which transform the representative of the conformal class non-trivially, hence do not fix (iii).

I will define notions of invisibility that apply to the two theories involved in a gauge–gravity duality in a moment.

Let a T-invisible diffeomorphism be a diffeomorphism that is invisible to theory T, in the sense of its preserving appropriate structures of theory T. Let us now proceed to specify these structures in more detail.

For the gravity theory, there are three related notions of gravity-invisibility, depending on which of the structures (i)–(iii) above are preserved, as follows:

• (a) strongly gravity-invisible diffeomorphisms: which fix all of (i)–(iii);

• (b) weakly gravity-invisible diffeomorphisms: which fix (i) & (ii) or (i) & (iii) but not necessarily all three;

• (c) (simpliciter) gravity-invisible diffeomorphisms: which fix (ii) & (iii) but not necessarily (i).

The notion of QFT-invisible diffeomorphisms, on the other hand, concerns the QFT: they are those gravity diffeomorphisms which cannot be seen (in a sense yet to be made precise) through the duality, hence are invisible to the QFT.

Thus, my definition of ‘invisibility of diffeomorphisms’ is relative to a theory (the gravity theory or the QFT): more precisely, relative to certain structures preserved within that theory. Thus the gravity-invisible diffeomorphisms are a priori independent of the duality, and express only a property of the gravity theory. The QFT-invisible diffeomorphisms will be the ones that should be seen as a property of the duality, viz. they are diffeomorphisms of the gravity theory which are invisible to the QFT (and they will be defined in terms of gravity-invisible diffeomorphisms).

The main mathematical results of this paper can then be summarised in the following three statements regarding infinitesimal diffeomorphisms (keeping the same numbering (a)–(c), since each result refers to its corresponding class above):

(a: Theorem 3, Sect. 2.2.1):

There exist no non-trivial strongly gravity-invisible diffeomorphisms, i.e. imposing that the diffeomorphism is strongly gravity-invisible also implies that it is equal to the identity.

(b: Propositions 1, 2, Sect. 2.2.1):

The weakly gravity-invisible diffeomorphisms reduce to conformal transformations at the boundary of the manifold.

(c: Sect. 2.4):

There exist non-trivial gravity-invisible diffeomorphisms.

These mathematical results have a number of surprising physical and philosophical consequences:

• (1) There is a version of Einstein’s hole argument for (generalised) anti-de Sitter (AdS) space: what we may call the ‘bulk argument’, introduced in De Haro et al. [14, Sect. 6]. The result (c) in the current paper implies that there is indeed a non-empty class of diffeomorphisms for which the bulk argument holds. And result (c) also characterises this class: as being smaller than one might expect.

• (2) The weakly gravity-invisible diffeomorphisms (b) give rise to the conformal symmetry of the gauge theory, with the implication that not all diffeomorphic structure in the gravity theory is invisible to the quantum field theory (QFT). This substantiates the claim in De Haro et al. [14, Sect. 5.1] that not all ‘gauge’ structure (in the philosopher’s sense) is invisible to the duality. Although the connection between the diffeomorphisms in the gravity theory and conformal invariance is familiar from the gauge–gravity literature, the class of diffeomorphisms which give rise to conformal transformations is in this paper found to be larger than the standard one in Imbimbo et al. [26] and Skenderis [36]: see the discussion following Eqs. (17) and (20).

• (3) The distinction between visible and invisible diffeomorphisms, worked out in mathematical detail here, underlies the discussion of background-independence in De Haro [11, Sects. 2.3.2–2.3.4]: and, in particular, it characterises two classes of diffeomorphisms to which a different analysis of background-independence applied, in De Haro [11, Sect. 2.3.3]. In that paper, these two cases were distinguished from each other and from yet another class, of ‘large’ diffeomorphisms: which do not preserve any of the pairwise structures defined here, and which I will not consider in this paper. The distinction of QFT-visibility versus QFT-invisibility also provides the basis of the discussion, in De Haro [11, Sect. 2.3.3], of the purported covariance of states and quantities. The violation of covariance for even boundary dimensions is given in Eq. (36).

• (4) Having a precise characterisation of the notions of visibility and invisibility of diffeomorphisms, it now becomes possible to meaningfully discuss whether, and how, diffeomorphisms emerge on the gravity side. One point that readily follows from (a)–(c) is that, despite the claims in the literature, there is no ‘emergence of diffeomorphisms’ tout court: for the visible and the invisible diffeomorphisms do not arise in anything like the same sense. I shall leave this question for the future.

My results provide a completely general derivation of the condition for a gravity diffeomorphism to give rise to a conformal transformation on the boundary, which, though perhaps known to the experts in the geometry of gauge–gravity dualities,⁴ has not appeared in print except in very special cases. So, the results here fill a gap in the literature: indeed, to my knowledge, the derivation of the condition for the diffeomorphisms to be conformal transformations, i.e. the gravity derivation of the QFT’s conformal Killing equation from the requirement of weak invisibility (Eq. (17) for the linear case, Eq. (23) for the non-linear case) has not appeared in the literature except for pure AdS [22, Eq. 18] and low-dimensional cases [8, Sects. III, IV].

1.2 Plan of the Paper

In Sect. 2, I introduce and develop the methods from conformal geometry that are needed to be able to define visibility and invisibility with the precision required for our purposes. I then prove the results (a)–(c), which provide the mathematical basis for: (1) and (2), which were discussed in De Haro et al. [14]; as well as (3), which was discussed in De Haro [11]. Three Appendices contain technical and illustrative examples of the relevant physics, and of how QFT-invisibility shows in these examples.

The notion of invisibility is motivated by a discussion by Horowitz and Polchinski [25, p. 12]: ‘the gauge theory variables... are trivially invariant under the bulk diffeomorphisms, which are entirely invisible in the gauge theory’ (my emphasis). It follows from the analysis in the current paper that not all gravity diffeomorphisms are in fact invisible to the gauge theory. As we saw in (c) above, there is a large class (larger than normally realised⁵) of diffeomorphisms of the gravity theory which are not invisible to the gauge theory: those that do not restrict to the identity map on the boundary, under which the gauge theory is not invariant but covariant at best (in the case of odd d), and non-invariant (because of an anomaly when d is even) at worst. Section 3 will specify the class of QFT-invisible diffeomorphisms: the specification of the class turns out to be subtle, and the class turns out to be smaller than often expected. In Sect. 4, I discuss and summarise the results.

Though I take the discussion by Horowitz and Polchinski as my motivation for considering invisibility, my definition of the notion differs from theirs, in that, as mentioned in the preamble of this section, it is relative to a specific theory: and so, I allow for diffeomorphisms that are invisible not only to the gauge theory, but also for diffeomorphisms that are invisible to the gravity theory (in the sense that they preserve the structures (i), (ii) or (iii)).

2 Visible Versus Invisible Diffeomorphisms

In this section, I prove the main mathematical results of the paper, (a)–(c) in Sect. 1, concerning three kinds of gravity-invisible diffeomorphisms. In Sect. 2.1, I will collect the definitions and theorem, from [18, 19], that will be used in the rest of the section. In Sect. 2.2, I will define the relevant notions of invisibility and derive two propositions and our main theorem about them: (a) that the class of non-trivial strongly-invisible diffeomorphisms is empty, as well as (b) weakly gravity-invisible diffeomorphisms reduce to boundary conformal transformations. In Sect. 2.4, I will prove that (c) the class of non-trivial gravity-invisible diffeomorphisms is non-empty and I will give bounds on the asymptotic behaviour that ensure that such diffeomorphisms in fact exist. I will use these results in Sect. 3 to define the notion of QFT-invisible diffeomorphisms, and I will explain how it relates to the gravity-invisible diffeomorphisms.

Throughout, we will be considering solutions of Einstein’s equation in $d+1$ dimensions in vacuum⁶ with a negative cosmological constant $\Lambda =-{d(d-1)\over 2\ell ^2}$, where $\ell$ is called the curvature radius:

$$\begin{aligned} {\text{ Ric }}[{\hat{g}}]+{d\over \ell ^2}\,{\hat{g}}=0, \end{aligned}$$

(1)

and ${\hat{g}}$ is the $(d+1)$-dimensional metric (as opposed to g, which will denote a d-dimensional metric: to be defined below) of any signature.

2.1 Poincaré Metrics and Normal Forms

Our aim in this subsection is to introduce the geometrical notions that will allow us to articulate, in Sect. 2.2, three related notions of invisibility of a diffeomorphism. To this end, I will first, in Sect. 2.1.1, introduce conformal manifolds. Then I will define the notion of conformal compactness: manifolds whose metric, roughly speaking, has a double pole at the boundary, but is otherwise smooth and nondegenerate at the boundary, which is itself a conformal manifold. Then I will require the metric on this conformally compact manifold to be of Poincaré type, and introduce some results about the normal form of this metric. In Sect. 2.1.2, I will discuss diffeomorphisms, both active and passive: which will allow us to discuss their invisibility in Sect. 2.2.

2.1.1 Conformal Manifolds and Poincaré Metrics

Definitions. ⁷ A conformal structure on a differentiable manifold M is an equivalence class of (pseudo)-Riemannian metrics, in which two metrics are equivalent if one is a positive smooth multiple of the other. We will denote a conformal class, i.e. such a conformal structure, by [g]. Thus, [g] consists of all metrics on M of the form $\Omega ^2\, g$, where $\Omega$ is any smooth, real-valued function on M. g is a smooth metric, called a representative of the conformal class [g].

Throughout this paper, M will be a smooth manifold of dimension $d\ge 2$, equipped with a conformal structure [g]. The representative g of the class will be a smooth pseudo-Riemannian metric of signature (p, q) on M, with $p+q=d$. A conformal manifold, then, is a pair (M, [g]) of a smooth manifold of dimension $d\ge 2$, equipped with a conformal structure, which is a choice of a conformal class of metrics of signature (p, q).

Let ${\hat{M}}$ be a manifold with boundary M, $\partial {\hat{M}}=M$. Pick a defining function for this boundary: a function $r\in C^\infty ({\hat{M}})$ which satisfies: (i) $r>0$ in the interior ${\hat{M}}_\mathrm{{int}}={\hat{M}}-M$, (ii) $r=0$ on M, and: (iii) $\text{ d }r\not =0$ on M.

We will be concerned with the behaviour near the boundary M of ${\hat{M}}$. Locally near $r=0$, ${\hat{M}}$ has the form of a product manifold. Thus we will consider an open neighbourhood of $M\times \{0\}\subset M\times \mathbb {R}_{\ge 0}$, where the defining function $r\in \mathbb {R}_{\ge 0}$ denotes the second factor.

Definition

A smooth metric ${\hat{g}}$ on the interior of ${\hat{M}}$, ${\hat{M}}_\mathrm{{int}}$, of signature $(p+1,q)$ is conformally compact, if: (i) $r^2{\hat{g}}$ extends smoothly to ${\hat{M}}$, and: (ii) $r^2{\hat{g}}|_M$ is nondegenerate (i.e. of signature $(p+1,q)$ also on M). A conformally compact metric ${\hat{g}}$ is said to have conformal infinity (M, [g]) if $r^2{\hat{g}}|_{TM}\in [g]$.

Definition

(Fefferman and Graham [19, Sect. 4.1]. A Poincaré metric for (M, [g]) is a conformally compact metric ${\hat{g}}$ of signature $(p+1,q)$ on ${\hat{M}}_\mathrm{{int}}$, where $M_\mathrm{{int}}$ is an open neighbourhood of $M\times \{0\}\subset M\times \mathbb {R}_{\ge 0}$, such that:

• (1) ${\hat{g}}$ has conformal infinity (M, [g]).

• (2) If d is odd or $d=2$, then ${\text{ Ric }}[{\hat{g}}]+{d\over \ell ^2}\,{\hat{g}}$ vanishes to infinite order along M.

If $d\ge 4$ is even, then ${\text{ Ric }}[{\hat{g}}]+{d\over \ell ^2}\,{\hat{g}}={{\mathcal {O}}}(r^{d-2})$, i.e. ${\text{ Ric }}[{\hat{g}}]+{d\over \ell }\,{\hat{g}}$ ‘vanishes up to terms of order’ $r^{d-2}$.

The same results apply if one considers metrics $\check{g}$ on ${\hat{M}}_\mathrm{{int}}$ of signature $(p,q+1)$ such that ${\text{ Ric }}[\check{g}]-{d\over \ell ^2}\,\check{g}$ vanishes to the stated order.

Definition

(based on Fefferman and Graham [19, Sect. 4.2]. A Poincaré metric ${\hat{g}}$ for (M, [g]) is said to be in normal form relative to g if:

$$\begin{aligned} {\hat{g}}={\ell ^2\over r^2}\left( \text{ d }r^2+g_r\right) , \end{aligned}$$

(2)

where $g_r$ is a 1-parameter family of metrics on M of signature (p, q), such that $g_0=g$.

There is an alternative form of a Poincaré metric in normal form, with formal asymptotics that is entirely equivalent. It is suggested by Fefferman and Graham’s [18] ambient space construction that originally motivated their work. There is a diffeomorphism $\chi _\ell :M\times \mathbb {R}_{\ge 0}\rightarrow M\times \mathbb {R}_{\ge 0}$, $\chi _\ell (x,r)=\left( x,\sqrt{\ell \rho }\right)$ bringing the above metric to the following form:

$$\begin{aligned} {\hat{g}}={\ell ^2\over 4\rho ^2}\,\text{ d }\rho ^2+{\ell \over \rho }\,g(x,\rho ), \end{aligned}$$

(3)

where $g(x,\rho )=g_{\sqrt{\ell \rho }}(x)$ is a 1-parameter family of metrics on M satisfying $g(x,0)=g(x)=g_{ij}(x)\,\text{ d }x^i\,\text{ d }x^j\in [g]$, for a coordinate system $(x^1,\ldots ,x^d)$ on M.

Theorem

[19, Sect. 4.5]. Let M and g be given as above. Then there exists an even (i.e. it is an even function of r) Poincaré metric ${\hat{g}}$ for (M, [g]) which is in normal form relative to g.

2.1.2 Diffeomorphisms

Let p be a point in a neighbourhood $\,{{\mathcal {U}}}_1$ of ${\hat{M}}$. Let $\varphi$ be a coordinate function on $\,{{\mathcal {U}}}_1$, i.e. there is a chart $(\,{{\mathcal {U}}}_1,\varphi )$, such that $\varphi :~\,{{\mathcal {U}}}_1\rightarrow \mathbb {R}^{d+1}$, viz. it assigns $p\mapsto \varphi (p)$. Call the point that $\varphi$ maps to, $X:=\varphi (p)\in \mathbb {R}^{d+1}$. Let $\,{{\mathcal {U}}}_2$ be another neighbourhood of ${\hat{M}}$ with coordinate chart $(\,{{\mathcal {U}}}_2,\psi )$, such that $\psi :~\,{{\mathcal {U}}}_2\rightarrow \mathbb {R}^{d+1}$, viz. an assignment $q\mapsto \psi (q)$. Call the point that $\psi$ maps to, $\tilde{X}:=\psi (q)\in \mathbb {R}^{d+1}$.

A diffeomorphism $\phi :~\,{{\mathcal {U}}}_1\rightarrow \,{{\mathcal {U}}}_2$ is a homeomorphism that assigns to p another point $q=\phi (p)$, $\phi :p\mapsto \phi (p)$, such that the map $\Phi :=\psi \circ \phi \circ \varphi ^{-1}:~\mathbb {R}^{d+1}\rightarrow \mathbb {R}^{d+1}$ between the respective coordinates, i.e. $(\Phi \circ \varphi )(p)=(\psi \circ \phi )(p)$, is invertible, and both $\Phi$ and $\Phi ^{-1}=\varphi \circ \phi ^{-1}\circ \psi ^{-1}$ are $C^\infty$. We can also write this condition in terms of invertibility and differentiability of the function $\tilde{X}=\Phi (X)$ on $\mathbb {R}^{d+1}$ and its inverse $X=\Phi ^{-1}(\tilde{X})$.

When $\,{{\mathcal {U}}}_1=\,{{\mathcal {U}}}_2$, so that $\phi :~\,{{\mathcal {U}}}\rightarrow \,{{\mathcal {U}}}$, we can take $\psi =\varphi$ and $\Phi =\psi \circ \phi \circ \psi ^{-1}$. Then X and $\tilde{X}$ correspond to different points in $\,{{\mathcal {U}}}$, in the same coordinate chart. Such a diffeomorphism is called active. In this paper we will construe all diffeomorphisms as active.

One can also consider passive diffeomorphisms, which are mere reparametrizations of the coordinates: one considers a single point p and two overlapping coordinate charts $\left( \,{{\mathcal {U}}}_1,\varphi \right)$, $\left( \,{{\mathcal {U}}}_2,\psi \right)$ such that $p\in \,{{\mathcal {U}}}_1\cap \,{{\mathcal {U}}}_2$. The map $\Phi :\mathbb {R}^{d+1}\rightarrow \mathbb {R}^{d+1}$, $\varphi (p)\mapsto \Phi (\varphi (p))=\psi (p)$, in other words $\Phi (X)=\tilde{X}$, is then taken to be differentiable. The formula is the same, but the meaning of the diffeomorphism is different: since X and $\tilde{X}$ now correspond to the same point $p\in \,{{\mathcal {U}}}_1\cap \,{{\mathcal {U}}}_2$, but expressed in different coordinate charts.

Proposition

(Diffeo) [19, Sect. 4.3] Let ${\hat{g}}$ be a Poincaré metric on ${\hat{M}}_\mathrm{{int}}$ for (M, [g]). Then there exists an open neighbourhood ${{\mathcal {U}}}$ of $M\times \{0\}\subset M\times \mathbb {R}_{\ge 0}$ on which there is a unique diffeomorphism $\phi :\,{{\mathcal {U}}}\rightarrow {\hat{M}}$ such that $\phi |_M$ is the identity map, and $\phi ^*{\hat{g}}$ is in normal form relative to g on $\,{{\mathcal {U}}}$.

So, when we work with Poincaré metrics, we only need to consider those that are in normal form.

2.2 Strongly Gravity-Invisible Diffeomorphisms are the Identity

In this subsection, I will introduce three related notions of gravity-invisibility, and prove my main results about them, viz. (a)–(c) in Sect. 1:

(a):

non-trivial strongly gravity-invisible diffeomorphisms do not exist;

(b):

weakly gravity-invisible diffeomorphisms reduce to boundary conformal transformations;

(c: in Sect. 2.4):

there exist non-trivial gravity-invisible diffeomorphisms.

Consider a Poincaré metric ${\hat{g}}$ for (M, [g]). By (Diffeo), we can, without loss of generality, take this metric to be in normal form relative to g in an open neighbourhood $\,{{\mathcal {U}}}$ of $M\times \{0\}\subset M\times \mathbb {R}_{\ge 0}$ ⁸.

Now consider a diffeomorphism $\phi$ of the manifold, and the pullback $\phi ^*{\hat{g}}$ of the metric that it gives rise to. Let $\phi :~\,{{\mathcal {U}}}\rightarrow \,{{\mathcal {U}}}$ be a diffeomorphism, defined as in Sect. 2.1.2. We will be interested in the class of diffeomorphisms that preserve the normal form of the metric. We will also impose various conditions on the asymptotic form of the diffeomorphism. This will be encapsulated in the idea of a diffeomorphism being invisible (in one or another of three related senses); and our first aim, roughly speaking, will be to prove that only the identity diffeomorphism is invisible. As mentioned, we will consider active diffeomorphisms, though similar considerations apply to the passive ones. Thus we set $\psi =\varphi$ in the definition of an active diffeomorphism, in Sect. 2.1.2. Let us start with some definitions.

Definition

Let ${\hat{g}}$ be a Poincaré metric for (M, [g]) in normal form. A diffeomorphism $\phi :\,{{\mathcal {U}}}\rightarrow \,{{\mathcal {U}}}$, where $\,{{\mathcal {U}}}$ is an open neighbourhood of $M\times \{0\}\subset M\times \mathbb {R}_{\ge 0}$, is said to be invisible relative to $({\hat{g}},M,g)$ (or strongly gravity-invisible) if it satisfies the following three conditions:

• (i)    (Invisible relative to ${\hat{g}}$)   :  $\phi ^*{\hat{g}}$ is in normal form relative to g.

• (ii)   (Invisible relative to M) :  $\phi |_{M\times \{0\}}=\text{ id }_{M\times \{0\}}$. This means that $\Phi (x,0)=(x,0)$.

• (iii) (Invisible relative to g)    :  $(\phi ^*g)(p)=g(p)$, i.e. $\phi$ is an isometry of M.

In (iii), $p\in M$ and $(\phi ^*g)(p)$ is induced from $(\phi ^*g_r)(p)=g_{\tilde{r}}(\phi (p))$ at $r=0$ ($g=g_0$ in (2)), where $\tilde{r}:=\Phi ^{d+1}(x,r)$, the last component of $\Phi (x,r)\in \mathbb {R}^{d+1}$, which in what follows we shall denote $\Phi ^r(x,r)$. Also, notice that (iii) is not trivially implied by (ii): for (ii) allows a non-trivial transformation of r, which we will parametrise as $\xi (x)$, and which is non-zero at the boundary and does transform g; whereas (iii) is the requirement that g does not transform.

If, under the above stated conditions, $\phi$ is invisible relative to (M, g), in the sense that (ii) and (iii) hold but not necessarily (i), then $\phi$ is said to be gravity-invisible.

We will also consider diffeomorphisms that are invisible relative to $({\hat{g}},g)$ (i.e. (i) and (iii) hold but not (ii) necessarily) or invisible relative to $({\hat{g}}, M)$ (i.e. (i) and (ii) hold but not (iii) necessarily): such $\phi$’s shall be collectively called weakly gravity-invisible (and it will not be important for us to distinguish between the latter two conditions).

Strongly gravity-invisible versus gravity-invisible will be the crucial contrast for our discussion in Sects. 3.1–3.2. Also, in this section we will prove that a strongly gravity-invisible diffeomorphism must be the identity. The proof does not use (Diffeo) but it will be based on two propositions that (a) are interesting for their own sake, and (b) will give us insight into the the notion of invisibility.

Definition

A diffeomorphism $\varphi _M$ on a manifold M is called a conformal transformation if its effect on the metric is to rescale it by some smooth, strictly positive function $\omega :M\rightarrow \mathbb {R}_{>0}$, such that $(\varphi _M^*\,g)(p)=\omega ^{-2}(p)\,g(p)$.

Definition

Let ${\hat{g}}$ be a Poincaré metric for (M, [g]) in normal form. A diffeomorphism $\phi :\,{{\mathcal {U}}}\rightarrow \,{{\mathcal {U}}}$, where $\,{{\mathcal {U}}}$ is an open neighbourhood of $M\times \{0\}$, is said to be a boundary-conformal diffeomorphism (or simply, to be boundary-conformal) if $\phi$ induces a conformal transformation on g, i.e. there is a smooth, strictly positive function $\Omega :{\hat{M}}\rightarrow \mathbb {R}_{>0}$ such that:

$$\begin{aligned} \phi ^*{\hat{g}}(p)|_{p\in M}=\Omega ^{-2}(p)\,{\hat{g}}(p)~. \end{aligned}$$

(4)

Definition

We will say that a diffeomorphism $\phi$ on ${\hat{M}}$ reduces to a boundary diffeomorphism $\varphi _M$ on M if $\phi |_{M\times \{0\}}=\varphi _M\times \text{ id }_{\{0\}}$.

Written in a coordinate patch, a diffeomorphism that reduces to a boundary diffeomorphism is one that satisfies: $\Phi (x,0)=(\tilde{x},0)$, where $\tilde{x}=\psi (\varphi _M(p))$ for $p\in M\subset M\times \{0\}$, and $x=\psi (p)$. This can be written as $\tilde{x}=\Psi (x)$ where $\Psi :=\psi _M\circ \varphi _M\circ \psi _M^{-1}:~\mathbb {R}^d\rightarrow \mathbb {R}^d$ and $\psi _M:=\psi |_M:~M\rightarrow \mathbb {R}^d\subset \mathbb {R}^d\times \{0\}$.

Notice that a diffeomorphism that reduces to the identity on M is invisible relative to M, i.e. it trivially satisfies condition (ii) above.

Let us also make a choice of coordinates on $\mathbb {R}^{d+1}$ in terms of which we will write the metric in the normal form (2). Define $(x,r):=X=\psi (p)$ and $(\tilde{x},\tilde{r}):=\tilde{X}=\psi (\phi (p))$. $\Phi$ is an invertible map. The diffeomorphism $X=\Phi ^{-1}(\tilde{X})$ is then written:

$$\begin{aligned} x^i= & {} \left( \Phi ^{-1}\right) ^i(\tilde{x},\tilde{r})\nonumber \\ r= & {} \left( \Phi ^{-1}\right) ^r(\tilde{x},\tilde{r}), \end{aligned}$$

(5)

where the superscript r denotes the $(d+1)$-th component.

In the rest of this section we will be considering diffeomorphisms that are either invisible relative to M, or reduce to a boundary diffeomorphism $\varphi _M$. In both cases, the diffeomorphism acts as the identity on the second factor of $M\times \{0\}$. This means that, in both cases, $r=0$ and $\tilde{r}=0$ each still parametrise the boundary. We will say that such a diffeomorphism fixes the location of the boundary.

Comment on the Identity Map Our condition (ii) of invisibility relative to M is $\phi _{M\times \{0\}}=\text{ id }_{M\times \{0\}}$, implying that $\tilde{x}=x$ and $\tilde{r}=0$. Thus these diffeomorphisms fix the points of M at $r=0$. This is a weaker condition than requiring that the diffeomorphism should go to the identity in a neighbourhood $U:=M\times [0,\epsilon )$, for $\epsilon >0$, of $M\times \{0\}$, i.e. $\phi |_{U}=\text{ id }_U$. The latter condition is stronger than (ii), and the former allows for diffeomorphisms which act nontrivially along the r-direction, $\tilde{r}=\lambda (x)\, r$, while fixing $r=0$. Such diffeomorphisms generate conformal transformations at the boundary, as we will see in Propositions 1 and 2, thus they do not fix g(p): and hence they do not imply (iii).

2.2.1 Infinitesimal Case

In this section we will consider infinitesimal diffeomorphisms, as follows:

(Infinitesimal) We only consider maps close to the identity map in $\,{{\mathcal {U}}}$: $\phi =\text{ id }_{\,{{\mathcal {U}}}}+\delta \phi +\cdots$ Written out for $\Phi$, this means that $\Phi ={\text{ id }}_{\mathbb {R}^{d+1}}+\psi \circ \delta \phi \circ \psi ^{-1}+\cdots =:\text{ id }_{\mathbb {R}^{d+1}}+\delta \Phi +\cdots$ in $\varphi (\,{{\mathcal {U}}})$. In the coordinates (5), we will write:

$$\begin{aligned} x^i=\left( \Phi ^{-1}\right) ^i(\tilde{x},\tilde{r})= & {} \tilde{x}^i+\xi ^i(\tilde{x},\tilde{r})\nonumber \\ r=\left( \Phi ^{-1}\right) ^r(\tilde{x},\tilde{r})= & {} \tilde{r}-\tilde{r}\,\xi (\tilde{x},\tilde{r}), \end{aligned}$$

(6)

where $\xi ^i$ and $\xi$ will be taken to be infinitesimal, and we will linearise all expressions in terms of them.

If an infinitesimal diffeomorphism is to fix the boundary, then we immediately find that $\xi (\tilde{x},0)$ must be regular near $\tilde{r}=0$ on $\psi (\,{{\mathcal {U}}})$, i.e. $\xi (\tilde{x},\tilde{r})=\tilde{r}^\alpha \,\xi (\tilde{x})+{{\mathcal {O}}}(\tilde{r}^{\alpha +1})$ for some $\alpha \ge 0$. The notation ${{\mathcal {O}}}(\tilde{r}^{\alpha +1})$ means ‘up to terms of order $\tilde{r}^{\alpha +1}$ and higher’. We will take the lowest value of $\alpha$ possible, viz. $\alpha =0$, so that to account for higher values of $\alpha$ one simply sets $\xi (\tilde{x})=0$. Thus r can be written as:

$$\begin{aligned} r= & {} \tilde{r}~\omega (\tilde{x})+{{\mathcal {O}}}(\tilde{r}^2)= \tilde{r}\left( 1-\xi (\tilde{x})\right) +{{\mathcal {O}}}(\tilde{r}^2), \end{aligned}$$

(7)

for $\omega (\tilde{x})$ and $\xi (\tilde{x})$ both smooth functions.

Let us now consider diffeomorphisms that are invisible relative to ${\hat{g}}$, i.e. $\phi ^*{\hat{g}}$ is in normal form relative to a metric g on the boundary manifold M. So, from (2), for a point $q=\phi (p)\in \,{{\mathcal {U}}}$, the following must hold:

$$\begin{aligned} \left( \phi ^*{\hat{g}}\right) _{ij}(p)= & {} {\ell ^2\over \tilde{r}^2}~{\tilde{g}}_{ij}(q) \end{aligned}$$

(8)

$$\begin{aligned} \left( \phi ^*{\hat{g}}\right) _{ir}(p)= & {} 0 \end{aligned}$$

(9)

$$\begin{aligned} \left( \phi ^*{\hat{g}}\right) _{rr}(p)= & {} {\ell ^2\over \tilde{r}^2}~. \end{aligned}$$

(10)

We will work out these three equations linearising in the diffeomorphisms $\delta \Phi$, as in (Infinitesimal).

Equation (10) reduces to: $\left( \partial r\over \partial \tilde{r}\right) ^2{1\over r^2}={1\over \tilde{r}^2}$. This can be integrated over the entire $\psi (\,{{\mathcal {U}}})$

$$\begin{aligned} r=\tilde{r}~\omega (\tilde{x})+{{\mathcal {O}}}(\xi _i^2)~. \end{aligned}$$

(11)

So the lowest-order expression that we obtained in (7) by assuming that $\xi (\tilde{x},\tilde{r})$ was regular at $r=0$, is actually valid on the entire domain $\varphi (\,{{\mathcal {U}}})$.

Next we write out (9). For this purpose, we use the just-obtained (11). We get the following result:

$$\begin{aligned} \partial _{\tilde{r}}\xi ^i(\tilde{x},\tilde{r})=\tilde{r}\,g^{ij}(\tilde{x},\tilde{r})\,\partial _j\xi (\tilde{x})+{{\mathcal {O}}}(\xi ^2,\xi _i^2)~. \end{aligned}$$

(12)

The reason for the dependence of $g^{ij}$ on $(\tilde{x},\tilde{r})$ rather than (x, r) is that the expression is already linear in $\xi , \xi ^i$, so (x, r) can be replaced with $(\tilde{x},\tilde{r})$ in the entire equation.

Finally we work out (8), again for infinitesimal diffeomorphisms:

$$\begin{aligned} \tilde{g}_{ij}(\tilde{x},\tilde{r})= & {} \left( 1+\xi (\tilde{x})\left( 2-\tilde{r}\,\partial _{\tilde{r}}\right) \right) g_{ij}(\tilde{x},\tilde{r})+\nabla _i(g)~\xi _j(\tilde{x},\tilde{r})\nonumber \\&+\nabla _j(g)~\xi _i(\tilde{x},\tilde{r})+{{\mathcal {O}}}(\xi ^2,\xi _i^2)~. \end{aligned}$$

(13)

It will be useful for later use to write this as:

$$\begin{aligned} \delta _{\phi ^{-1}} \,g_{ij}(x,r):= & {} (\phi ^*g)_{ij}(x,r)-g_{ij}(x,r) \nonumber \\= & {} \xi (x)\left( 2- r\,\partial _{r}\right) g_{ij}(x,r)+\nabla _i\,\xi _j(x,r)+\nabla _j\,\xi _i(x,r)+{{\mathcal {O}}}(\xi ^2,\xi _i^2),\nonumber \\ \end{aligned}$$

(14)

where the tildes were dropped from the point (x, r). The expression is the same to linear order in the diffeomorphism because the difference of metrics is already of linear order.

Proposition 1

(Infinitesimal version) Let ${\hat{g}}$ be a Poincaré metric for (M, [g]) in normal form. If $\phi :\,{{\mathcal {U}}}\rightarrow \,{{\mathcal {U}}}$ is invisible relative to $({\hat{g}},g)$ and reduces to $\varphi _M$, then $\varphi _M$ is a conformal transformation.

To prove this, we take the expression (14) which was obtained from requirement that $\phi$ be invisible relative to ${\hat{g}}$ in (8)–(10). Requiring that $\phi$ be invisible relative to g as well, instructs us to set $(\phi ^* g)(p)= g(p)$, which is setting $\delta _{\phi ^{-1}}\, g_{ij}(x,0)=0$. Thus, setting $r=0$ in (14), this reduces to:

$$\begin{aligned} \delta _{\phi ^{-1}}\, g_{ij}(x)= & {} 2\xi (x)\,g_{ij}(x)+\nabla _{i}\,\xi _{j}(x) +\nabla _{j}\,\xi _{i}(x)+{{\mathcal {O}}}\left( \xi ^2,\,\xi _i^2\right) \nonumber \\= & {} 2\xi (x)\,g_{ij}(x)+({{\mathcal {L}}}_\xi g)_{ij}(x) +{{\mathcal {O}}}\left( \xi ^2,\xi _i^2\right) =0, \end{aligned}$$

(15)

where $\xi _i(x):=\xi _i(x,0)$ and ${{\mathcal {L}}}_\xi g$ is the Lie derivative with respect to the vector field $\xi$ on M (not to be confused with the scalar function $\xi (x)$). Taking the trace of the above equation, and substituting the result back into the same equation, we get:

$$\begin{aligned} \xi (x)= & {} -{1\over d}\,\nabla ^i\,\xi _i(x)+{{\mathcal {O}}} \left( \xi ^2,\,\xi _i^2\right) \end{aligned}$$

(16)

$$\begin{aligned} \delta _{\phi ^{-1}} g_{ij}(x)= & {} {{\mathcal {L}}}_\xi \,g_{ij}(x)-{2\over d}\,g_{ij}(x)\,\nabla ^k\,\xi _k+{{\mathcal {O}}} \left( \xi ^2,\,\xi _i^2\right) =0~. \end{aligned}$$

(17)

This is precisely the conformal Killing equation, i.e. the infinitesimal version of the condition for $\varphi _M^{-1}$ (and hence $\varphi _M$) to be a conformal transformation. $\square$

As discussed in Sect. 1, the Killing equation (17) on M has, hitherto, been derived only in very special cases such as pure AdS space (cf. [22, Eq. (18)])). The reason is that the more general treatments, like Imbimbo et al. [26, Sect. Eq. (2.6)] and Skenderis [36, Sect. Eq. (8)], assume that $\xi _i(x)=0$, and hence they cannot get the Killing equation.

Equation (17) can be rearranged as follows:

$$\begin{aligned} \delta _{\varphi _M^{-1}}\,g(x)={{\mathcal {L}}}_\xi \,g(x)=-{2\over d}\,\nabla ^k\xi _k(x)~g(x), \end{aligned}$$

(18)

which is indeed the infinitesimal version of the following exponential form:

$$\begin{aligned} (\varphi ^{-1}_M)^*\,g(x)=e^{-2\xi (x)}\,g(x)~. \end{aligned}$$

(19)

We will give a proof of this formula for finite diffeomorphisms at the end of this subsection.

Proposition 2

(Infinitesimal version) Let ${\hat{g}}$ be a Poincaré metric for (M, [g]) in normal form. If $\phi :\,{{\mathcal {U}}}\rightarrow \,{{\mathcal {U}}}$ is invisible relative to $({\hat{g}},M)$, then $\phi$ reduces to a Weyl transformation.

To prove this, notice that the requirement of invisibility relative to M means that we have to set $\xi ^i(x,0)=0$. But then we automatically get, from the requirement (14) that $\phi$ be invisible relative to ${\hat{g}}$, that $\delta _{\phi ^{-1}}\,g_{ij}(x,r)|_{r=0}=2\xi (x)\,g_{ij}(x)=(\phi ^*g)_{ij}(x)-g_{ij}(x)$. This is indeed an infinitesimal Weyl transformation. $\square$

The finite version of the above is:

$$\begin{aligned} \phi ^*g=e^{-2\xi (x)}\,g~. \end{aligned}$$

(20)

This is the kind of Weyl transformation obtained in the standard accounts, see e.g. [36, Eq. 10]: it is generated by the scalar $\xi (x)$, assuming that $\xi ^i(x,0)=0$.

Theorem 3

Let ${\hat{g}}$ be a Poincaré metric for (M, [g]) in normal form. If $\phi :\,{{\mathcal {U}}}\rightarrow \,{{\mathcal {U}}}$ is invisible relative to $({\hat{g}},M,g)$, then $\phi$ is the identity.

If $\phi$ is invisible relative to M then $\xi _i(x)=0$, as we saw in Proposition 2. But since it is also invisible relative to g then also $\xi (x)=0$, from (16). Since (11) was valid over the entire $\psi (\,{{\mathcal {U}}})$, then $r=\tilde{r}$ over the entire $\psi (\,{{\mathcal {U}}})$.

In order to show that $\phi$ is the identity, since we already know that $\xi ^i(x,0)=0$, it is enough to show that the first derivative of $\xi ^i(x,r)$ vanishes everywhere on $\,{{\mathcal {U}}}$. This now readily follows from (12) because the right-hand side now identically vanishes. $\square$

2.2.2 Finite Diffeomorphisms

Let ${\hat{g}}$ be a Poincaré metric for (M, [g]) in normal form. Let $\phi :\,{{\mathcal {U}}}\rightarrow \,{{\mathcal {U}}}$ be a finite diffeomorphism, invisible relative to ${\hat{g}}$. We use the same notation as before:

$$\begin{aligned} r= & {} \tilde{r}~\omega (\tilde{x},\tilde{r})\nonumber \\ x^i= & {} \tilde{x}^i+\xi ^i(\tilde{x},\tilde{r})~. \end{aligned}$$

(21)

The generalisations of (8)–(10) in terms of these variables are as follows:

$$\begin{aligned} {\partial x^k\over \partial \tilde{x}^i}{\partial x^l\over \partial \tilde{x}^j}~g_{kl}\left( x(\tilde{x},\tilde{r}),r(\tilde{x},\tilde{r})\right) +\tilde{r}^2\,\partial _i\omega (\tilde{x},\tilde{r})\partial _j\omega (\tilde{x},\tilde{r})= & {} \omega ^2(\tilde{x},\tilde{r})~\tilde{g}_{ij}(\tilde{x}, \tilde{r})\nonumber \\ \partial _{\tilde{r}} \xi ^k~{\partial x^l\over \partial \tilde{x}^i}\,g_{kl}\left( x(\tilde{x},\tilde{r}),r(\tilde{x},\tilde{r})\right) +{1\over 2}\,\,\tilde{r}\,\tilde{\partial }_i\left( \omega ^2(\tilde{x},\tilde{r})\right)= & {} 0\nonumber \\ \partial _{\tilde{r}}\,\xi ^i\partial _{\tilde{r}}\xi ^j\,g_{ij}\left( x(\tilde{x},\tilde{r}),r(\tilde{x},\tilde{r})\right) +\tilde{r}^2\,(\partial _{\tilde{r}}\omega )^2+\tilde{r}\,\partial _{\tilde{r}}(\omega ^2(\tilde{x},\tilde{r}))= & {} 0, \end{aligned}$$

(22)

(Setting $\tilde{r}=0$, the last equation implies that, if the metric is Riemannian rather than pseudo-Riemannian, then $\partial _{\tilde{r}}\xi ^i|_{\tilde{r}}=0$. The same requirement is obtained for pseudo-Riemannian metrics from the requirement that the induced metric does not change: see Sect. 2.4. But we will not need this.)

Let us now assume that ${\hat{g}}$ is invisible relative to g as well. Invisibility relative to g gives:

$$\begin{aligned} {\partial x^k\over \partial \tilde{x}^i}{\partial x^l\over \partial \tilde{x}^j}~g_{kl}(x(\tilde{x}))=\omega ^2(\tilde{x})~g_{ij}(x(\tilde{x})), \end{aligned}$$

(23)

where $\omega (\tilde{x}):=\omega (\tilde{x},0)$. This is the analog of Proposition 2: the diffeomorphisms reduce to a boundary Weyl transformation.

Finally, if, in addition, ${\hat{g}}$ is invisible relative to M, so $x^i|_{\tilde{r}=0}=\tilde{x}^i$, then it follows that $\omega (x)=+1$ (the plus sign chosen so as to preserve the orientation). That is, if the diffeomorphism along M is the identity, then also the diffeomorphisms along the normal direction are the identity. This is the generalisation of Proposition 1.

2.3 Two Classes of Weakly-Gravity Invisible Diffeomorphisms

In this section, I will compare the weakly-gravity invisible diffeomorphisms, obtained in Sect. 2.2, to the physics literature.⁹

The weakly gravity-invisible diffeomorphisms comprised two distinct classes: on the one hand, the diffeomorphisms invisible relative to $({\hat{g}},g)$, i.e. satisfying (i) and (iii); on the other, the ones invisible relative to $({\hat{g}},M)$, i.e. satisfying (i) and (ii). The former class gave rise to conformal transformations of the boundary manifold, i.e. coordinate transformations at the boundary, satisfying the Killing equation (18). The latter class gave rise to Weyl transformations, i.e. local rescalings of the metric of the boundary manifold.

These two classes are of course different, as diffeomorphisms of the metric ${\hat{g}}$: even if their effects, on the metric g induced on the boundary, are similar—they both give rise to a local rescaling of the metric. The two classes are conceptually distinct: the former class is a coordinate transformation of the boundary manifold, whereas the latter class is a choice of a different representative of the conformal class of the metric. I now compare these two classes to the physics literature.

Diffeomorphisms of the former class, i.e. invisible relative to $({\hat{g}},g)$, are, to lowest order, of the type (cf. Proposition 1 in Sect. 2.2.1):

$$\begin{aligned} x^i= & {} \tilde{x}^i+\xi ^i(x)\nonumber \\ r= & {} \tilde{r}\left( 1-\xi (x)\right) , \end{aligned}$$

(24)

where $\xi (x)=-{1\over d}\,\nabla ^i\xi _i(x)$, and $\xi ^i(x)$ satisfies the Killing equation ${{\mathcal {L}}}_\xi \,g_{ij}(x)={2\over d}\,g_{ij}(x)\,\nabla ^i\xi _k$. Thus they correspond to conformal transformations at the boundary, i.e. coordinate transformations of the boundary manifold which give rise to Weyl transformations of the metric. The Killing equation is the necessary and sufficient condition that they be Weyl transformations.

When restricted to pure AdS, this class is identical with the diffeomorphisms investigated in Gubser et al. [22, Sect. 2.1]. These authors use the notation z for my r, $\zeta ^\mu$ for my $\xi ^i(\tilde{x},\tilde{r})$, and $\xi ^\mu$ for my $\xi ^i(\tilde{x})$. Their $\xi ^z$ corresponds to my $\xi (x)$. One easily verifies that their Eq. (16) corresponds to my Eqs. (12) and (16).

Diffeomorphisms of the latter class, i.e. invisible relative to $({\hat{g}},M)$, are, to lowest order, of the type (cf. Proposition 2 in Sect. 2.2.1):

$$\begin{aligned} x^i= & {} \tilde{x}^i\nonumber \\ r= & {} \tilde{r}\left( 1-\xi (x)\right) , \end{aligned}$$

(25)

where now $\xi (x)$ is an arbitrary smooth function, and there are no diffeomorphisms tangent to the boundary.¹⁰

This class of diffeomorphisms corresponds to the one in Imbimbo et al. (1999: Sect. 2). These authors use the coordinate $\rho$ in Eq. (3), rather than the coordinate r I have used in Eq. (2) and in Sect. 2.2.¹¹ The change of coordinates is given by $\rho =r^2/\ell$. One then easily checks that their Eq. (2.2), with their choice of boundary condition $a^i(x,\rho =0)=0$, is exactly Eq. (25). And it is in fact this choice of boundary condition that prevents them to finding the diffeomorphisms corresponding to Eq. (24) and the Killing equation.

The difference between the two cases is the structures they preserve. The first class preserves ${\hat{g}}$ and g, i.e. in particular, $\delta _{\phi ^{-1}}g_{ij}(x)=0$. For pure AdS, this amounts to considering bulk diffeomorphisms that leave the flat boundary metric (Euclidean or Minkowski) fixed. This means that the Weyl rescalings of the boundary metric and the coordinate transformations along the boundary directions must cancel each other out. This is the case for Eq. (25), under the conditions stated. The condition for the second class is that it preserves ${\hat{g}}$ and M, and the latter condition sets the components of the diffeomorphisms parallel to the boundary to zero, i.e. $\xi ^i(x,0)=0$. However, Weyl transformations are still allowed.

It is not surprising that the two classes of diffeomorphisms, Eqs. (24) and (25), are only connected at the identity: since they are defined by the different structures that they preserve. By ‘connected at the identity’, I here mean that one cannot simply set $\xi ^i(x)=0$ in Eq. (24) to get Eq. (25), because then also $\xi (x)=0$, and then the diffeomorphism is the identity. This is of course the content of Theorem 3.

2.4 Gravity-Invisible Diffeomorphisms Exist

In Theorem 3 of Sect. 2.2, we proved that there are no strongly gravity-invisible diffeomorphisms close to the identity (i.e. infinitesimal).¹² The strongly gravity-invisible diffeomorphisms form a natural class to consider because, though they preserve the normal form of the metric, they are not isometries of the $(d+1)$-dimensional metric: they are only isometries of the boundary conformal structure. Notice that the normal form of the metric corresponds to what physicists call a ‘radial gauge’, i.e. a choice of coordinates such that ${\hat{g}}_{ir}=0$. Thus, the strongly gravity-invisible diffeomorphisms preserve this gauge condition in addition to the two other invisibility conditions. We have shown that this class is trivial.

In this subsection we study the non-trivial class of gravity-invisible diffeomorphisms: those that are invisible relative to (M, g). In the next section I will comment on the holographic interpretation of these gravity-invisible diffeomorphisms, as giving rise to QFT-invisible diffeomorphisms.

Our starting point is to rewrite the diffeomorphism in a form similar to (6):

$$\begin{aligned} r= & {} \tilde{r}-\xi (\tilde{x},\tilde{r})\nonumber \\ x^i= & {} \tilde{x}^i+\xi ^i(\tilde{x},\tilde{r})~. \end{aligned}$$

(26)

In order for $\phi |_{M\times \{0\}}=1$, we must preserve the boundary $r=0$, i.e. we must take¹³ $\xi (\tilde{x},\tilde{r})=\tilde{r}^\alpha \,\xi (\tilde{x})+{{\mathcal {O}}}(\tilde{r}^{\alpha +1})$, $\xi ^i(\tilde{x},\tilde{r})=\tilde{r}^\beta \,\xi ^i(\tilde{x})+{{\mathcal {O}}}(\tilde{r}^{\beta +1})$, with $\alpha \ge 1$ and $\beta \ge 0$. I work to linear order in $\xi ,\xi ^i$ throughout. The metric ${\hat{g}}$ in (2) is modified as follows:

$$\begin{aligned} (\phi ^*{\hat{g}})_{ij}= & {} {\ell ^2\over \tilde{r}^2}\left( \left( 1+\xi (\tilde{x},\tilde{r})\,\left( {2\over \tilde{r}}-\partial _{\tilde{r}}\right) \right) \,g_{ij}(\tilde{x},\tilde{r})+\nabla _i\xi _j+\nabla _j\xi _i\right) \nonumber \\ (\phi ^*{\hat{g}})_{ir}= & {} {\ell ^2\over \tilde{r}^2}\left( -\partial _i\xi (\tilde{x}, \tilde{r})+g_{ik}(\tilde{x},\tilde{r})\,\partial _{\tilde{r}}\xi ^k(\tilde{x},\tilde{r})\right) \nonumber \\ (\phi ^*{\hat{g}})_{rr}= & {} {\ell ^2\over \tilde{r}^2}\left( 1-2\,\partial _{\tilde{r}}\xi (\tilde{x},\tilde{r})+{2\over \tilde{r}}\,\xi (\tilde{x},\tilde{r})\right) \end{aligned}$$

(27)

where $\xi _i:=g_{ij}(\tilde{x},\tilde{r})\,\xi ^j(\tilde{x}, \tilde{r})$, and the covariant derivatives are with respect to the metric $g(\tilde{x},\tilde{r})$. Of course, if $\alpha =1$ and $\beta =0$, the first formula agrees with the earlier result (8) and (13) when $\xi$, $\xi ^i$ are expanded in $\tilde{r}$.

The gravity-invisible diffeomorphisms are only invisible relative to (M, g) not the metric ${\hat{g}}$ on ${\hat{M}}$. So, we only need to demand that $\phi$ is an isometry of the induced metric, obtained from the first of (27) multiplying by a factor of $r^2/\ell ^2$. We obtain the condition, at $r=0$:

$$\begin{aligned} g_{ij}(x,r)|_{r=0}= \left( 1-\xi (\tilde{x},\tilde{r})\,\partial _{\tilde{r}}\right) g_{ij}(\tilde{x},\tilde{r})|_{r=0}+\nabla _i\,\xi _j(\tilde{x},\tilde{r})|_{r=0}+\nabla _j\,\xi _i(\tilde{x},\tilde{r})|_{r=0}~.\nonumber \\ \end{aligned}$$

(28)

Let us now set $\xi (\tilde{x},\tilde{r})=\tilde{r}^\alpha \,\xi (\tilde{x})$, $\xi ^i(\tilde{x},\tilde{r})=\tilde{r}^\beta \,\xi ^i(\tilde{x})$, set $r=0$, and use the fact that the first derivative of the metric is zero at lowest order in r.

Table 1 Table showing when an invisible diffeomorphism exists

For $\beta =0$, we find that the diffeomorphism is invisible unless

$$\begin{aligned} \nabla _i\,\xi _j(\tilde{x})+\nabla _j\,\xi _i(\tilde{x})=0, \end{aligned}$$

(29)

i.e. unless $\xi _i(\tilde{x})$ is an isometry of the representative of the boundary conformal structure g. For $\beta \ge 1$, we find that the diffeomorphism is always invisible.

Let us consider a slightly stronger invisibility condition, namely that $(\phi ^*{\hat{g}})_{ir}$, up to its conformal factor, should remain zero at $r=0$. This corresponds to the normal form of the metric (i) being preserved asymptotically. This requirement gives us the additional condition that $\xi _i(\tilde{x})=0$ when $\beta =1$ in order to have an invisible diffeomorphism. The results are summarised in the table in Table 1. However this will not encumber the exposition in what follows. Since the additional condition is minimal, for it does not affect the other values of $\beta$, when I discuss the physics of gauge–gravity dualities, I will still use g instead of $\gamma$ for the induced metric, and will refer to the gravity-invisible diffeomorphisms as those that are invisible relative to (M, g).

In the gravity literature, the induced metric on any d-dimensional timelike hypersurface inside a $(d+1)$-dimensional volume is defined as: $\gamma _{\mu \nu }:=g_{\mu \nu }-n_\mu n_\nu$, where $n_\mu$ is a normal covector to the hypersurface (see e.g. Wald [40], p. 255) for the spacelike case). Of course, this metric and ${\hat{g}}$ both give rise to the same induced metric $r=0$, and they give exactly the same invisibility conditions that we just obtained. This is shown in Appendix A.

In summary, there is an invisible diffeomorphism $\phi$ (relative to M and g) for $\beta =0,1$ if ${{\mathcal {L}}}_\xi \,g=0$, resp. $\xi _i=0$. This diffeomorphism is then generated by $\xi (\tilde{x})$. For $\beta \ge 2$, there is an invisible diffeomorphism (relative to M and g) for any smooth $\xi$, $\xi ^i$. See the table in Table 1.

3 Invisibility in Gauge–Gravity Dualities

In the previous section, I derived two propositions and a theorem amounting to points (a)–(c) in Sect. 1. These results led to the definition, in Sect. 2.4, of gravity-invisible diffeomorphisms as those diffeomorphisms which are invisible relative to (M, g). In this section, I turn to the physical relevance of gravity-visible and gravity-invisible diffeomorphisms for gauge–gravity dualities.¹⁴ For an introduction to gauge–gravity dualities, see Ammon and Erdmenger [1]. A conceptual introduction is in De Haro et al. [15].

The important question for gravity-visible and gravity-invisible diffeomorphisms, discussed in the previous section, in connection with dualities, is whether they are also visible or invisible to the QFTs which are dual to the relevant gravity theories. To answer this question, we first need to discuss what the relevant gravity theory is. The definitions of invisibility in Sect. 2.2, from which the propositions about gravity-invisibility and weak gravity-invisibility were derived, involve Poincaré metrics, which satisfy Einstein’s equations in vacuum with a negative cosmological constant, Eq. (1), up to a specified order of approximation. The 1-parameter family of metrics $g_r$ on M in (2) has an expansion of the form [19, Theorem 4.8]:

$$\begin{aligned} g_r=\sum _{N=0}^\infty g_{r}^{(N)}\left( r^d\log r\right) ^N, \end{aligned}$$

(30)

where each of the $g_{r}^{(N)}$ is a smooth family of metrics on M even in r. Of particular interest is the term $N=0$, with its even expansion in r:

$$\begin{aligned} g_r^{(0)}=g_{(0)}+r^2\,g_{(2)}+r^4\,g_{(4)}+\cdots , \end{aligned}$$

(31)

and it follows from (30) that $g_{(0)}=g_0=g$.

For odd d, all $g_{r}^{(N)}$ with $N\ge 1$ vanish, and only the $N=0$ term contributes: the above is then an even power series around $r=0$, and the solution is determined uniquely to infinite order given $g_{(0)}$ and $g_{(d)}$. Namely:

• All $g_{(n)}$ are determined algebraically from Einstein’s equations (except for $g_{(0)}$ and $g_{(d)}$): they are given by covariant expressions involving $g_{(0)}$ and $g_{(d)}$ and their derivatives.

• The coefficients $g_{(0)}$ and $g_{(d)}$ are not determined by Einstein’s equations (only the trace and divergence of $g_{(d)}$ are determined): they are initial data.

• One recovers pure AdS when $g_{(0)}$ is chosen to be flat (i.e. a flat Minkowski metric). In that case, all higher coefficients in the series (31) vanish.

For even d, the logarithmic terms are nonzero, but again the entire $g_r$ is determined to infinite order given the same two data. In this expansion, Einstein’s equations become algebraic equations relating the coefficients in the expansion (31) for $g_r^{(N)}$ to $g_{(0)}$, $g_{(d)}$ and their derivatives.

Thus, the discussion in Sect. 2 is relevant for the asymptotic solutions of Einstein’s equations near the boundary of an Einstein space,¹⁵ where the metric induced on the boundary is arbitrary. Furthermore, the formal series (30) converges if the boundary conditions $g_{(0)}$ and $g_{(d)}$ are real-analytic functions of the boundary coordinates x [19, pp. 4, 49].

As is well-known in the gauge–gravity literature (see e.g. [13, Sect. 1], general relativity is a good approximation to the full string- or M-theory near $r=0$. As r increases, new terms may be needed in the action (see the discussion in Sect. 3.1). In particular, all the asymptotic expansions used in the previous section (Eqs. (6), (7), as well as the formulas evaluated at $r=0$) are good approximations as long as the size of the neighbourhood $\,{{\mathcal {U}}}\!$ is much smaller than the scale set by the radius of curvature. This means that the techniques developed here indeed give good approximations to the quantities of interest in gauge–gravity dualities, such as the holographic stress-energy tensor.

In other words, the visible and invisible diffeomorphisms discussed in Sect. 2 are indeed relevant to the gravity side of gauge–gravity dualities. In Sect. 3.1, I will argue that gravity-invisible diffeomorphisms are invisible to the dual QFT, so they are also ‘QFT-invisible’, and ‘duality-invisible’. In two Appendices B and C, I give explicit physics examples of the kinds of QFT quantities which are invisible, and discuss generalisations of these concepts to the case including bulk matter. In Sect. 3.2, I discuss how the weakly gravity-invisible diffeomorphisms are seen by the QFT, hence are QFT-visible.

3.1 Gravity-Invisible Diffeomorphisms are QFT-Invisible

In this subsection, I will discuss the sense in which gravity-invisible diffeomorphisms leave the gauge theory invariant, hence are ‘QFT-invisible’. On the conception of duality expounded in De Haro et al. [14, Sect. 3.3], in order for invisible diffeomorphisms to be ‘gauge’ in the philosophers’ sense, they should leave all the quantities of the theory, evaluated on the states, invariant. As discussed, our theory is a theory of pure gravity: so our task now is to define the quantities that need to be evaluated.

The gauge–gravity duality isomorphism is often called a ‘dictionary’, because it ‘translates’ gravity to QFT quantities, and viceversa. This dictionary identifies the renormalized classical action with the generating functional of the QFT (in a suitably taken ’t Hooft limit, see [1, pp. 180–182]. For a theory of pure gravity without matter, the renormalized action is a functional (as usual, indicated by square brackets) of the representative g of the boundary conformal structure, and nothing else (for more details, see Sect. 3.2):

$$\begin{aligned} S_\mathrm{{ren}}[g]\equiv W_\mathrm{{QFT}}[g]~. \end{aligned}$$

(32)

In such a gravity theory with a boundary at spatial infinity, the basic classical physical quantity is the renormalised quasi-local stress-energy tensor $\Pi$ [9, 13], which is evaluated by taking the derivative of (32) with respect to the representative g of the boundary conformal structure. But by the dictionary, (the one-point function of) this stress-energy tensor is precisely the 1-point function of the renormalized stress-energy tensor of the dual QFT at the fixed point, evaluated from the generating functional $W_\mathrm{{QFT}}[g]$! (for more details, see Sect. 6.1.2 of De Haro et al. [15]). That is:

$$\begin{aligned} \langle \Pi _{ij}\rangle _g\equiv \langle T_{ij}[g](x)\rangle _\mathrm{{QFT}}={2\over \sqrt{g}}\,{\delta W_\mathrm{{QFT}}[g]\over \delta g^{ij}}={d\,\ell ^{d-1}\over 16\pi G_\mathrm{{N}}}\,g_{(d)ij}(x)+\text{(local } \text{ terms) },\quad \quad \end{aligned}$$

(33)

and the subscript g indicates the fact that we are evaluating this expression on a state determined by the conformal class [g] at the boundary. The first term on right-hand side of the above equation is the term appearing at order $r^d$ in the asymptotic expansion of the metric g(x, r) (31) in powers of r. The local terms are given in De Haro et al. ([13, Eq. (1.3)] and subsequent discussion).

A calculation like (33) can be done for CFTs whose only gauge invariant, local, renormalizable operators are built from their stress-energy tensor T[g] only, for various representatives g of conformal classes. By the state-operator correspondence which holds at the fixed point (cf. e.g. [15, Sect. 3]), further states are obtained by multiplying the reference state corresponding to [g] with further powers (even exponentials) of the stress-energy tensor.¹⁶

Will the gravity-invisible diffeomorphisms preserve the 1-point function (33)? Since $W_\mathrm{{QFT}}[g]$ is a functional of g, it must, in fact, be invariant under them. Of course, the stress-energy tensor is known to be anomalous, for even values of d, under conformal transformations of g, so that there is a dependence of the representative of the class chosen.¹⁷ This will be our concern in Sect. 3.2. But, for the gravity-invisible diffeomorphisms that we are considering here (cf. Sect. 1, “fix (ii)” and “fix (iii)”), g is simply invariant, and therefore so is the generating functional.

There is an important question here, which relates to the passage from Horowitz and Polchinski [25, Sect. 1.3.2] quoted at the end of the Introduction: ‘the gauge theory variables... are trivially invariant under the bulk diffeomorphisms, which are entirely invisible in the gauge theory.’ Does my argument amount to saying that the generating functional $W_\mathrm{{QFT}}[g]$ is trivially invariant under the gravity diffeomorphisms? I submit that it does not amount to that. One important aspect of the non-triviality will appear when we discuss the higher-point functions in the paragraphs below—the dependence on the gravity metric is highly non-trivial: for the invisibility argument requires ensuring that $g_{(d)}$ is a functional of [g] and [g] only, i.e. it requires having a global solution, of which not many are known (some examples will be given in Appendix B). But leaving this issue aside for the moment, and more importantly for the identification of the (simpliciter) gravity-invisible diffeomorphisms as QFT-invisible diffeomorphisms, we must ask: to what extent does the above ‘invisibility argument’ about $W_\mathrm{{QFT}}[g]$ require both conditions (ii) and (iii) in Sect. 2.2 to obtain? Could we enlarge the class of QFT-invisible diffeomorphisms to contain the whole of (ii) or the whole of (iii) (or even their union!), rather than their intersection? Naively, one might be inclined to think that this is possible because both conditions should leave g invariant: (ii) is the condition $\phi |_{M\times \{0\}}=0$, which in particular implies $\xi ^i(\tilde{x},0)=0$ (where $\xi ^i(\tilde{x},\tilde{r})$ is defined in Eq. (6)), and this means that there are no coordinate transformations on the boundary being induced. As for (iii), this is the condition $\phi ^*g=g$, which implies that $\delta _{\phi ^{-1}}g_{ij}=2\xi \,g_{ij}+\nabla _i\,\xi _j+\nabla _j\,\xi _i=0$, and so the total effect on g cancels out.

But notice that the correct condition of QFT-invisibility is not that g should not transform but rather that the diffeomorphism itself should be invisible to the QFT: it should not act on the QFT variables at all. In the case of (ii), setting $\xi ^i(\tilde{x},0)=0$ still allows for $\phi$ inducing a Weyl transformation on g, so that a diffeomorphism satisfying just (ii) is certainly QFT-visible. As for (iii), we still have non-trivial transformations $\xi ,\xi _i$ which now jointly act on the boundary QFT variables. $\xi _i$ acts as a boundary coordinate transformation and $\xi$ acts as a Weyl transformation (rather than a conformal transformation) but just so that their combined effects cancel each other out. So, these diffeomorphisms are visible to the QFT, since they act on it as different transformations, even if, as a result of their combined effects, g is left invariant under them. An additional reason not to classify diffeomorphisms fixing (iii) but not (ii) as QFT-invisible is that, if the generating functional $W_\mathrm{{QFT}}[g]$ depends on other (matter) couplings, the combined transformation of the matter couplings will not cancel out like they do for the metric, unless further transformations for the couplings are assumed—thus rendering the transformation, again, visible. In other words, (ii) and (iii) are both jointly needed if the diffeomorphisms are truly to qualify as QFT-invisible, rather than g being ‘trivially invariant’ under them. Thus, the (simpliciter) gravity-invisible diffeomorphisms are—in so far as the 1-point function is concerned—the correct candidates for QFT-invisible diffeomorphisms.

The argument extends to higher-point correlation functions of the stress-energy tensor:

$$\begin{aligned} \langle T_{ij}(x_1)\cdots T_{kl}(x_n)\rangle ={2^n\over \sqrt{g(x_1)\cdots g(x_n)}}~{\delta ^{(n)}W[g]\over \delta g^{ij}(x_1)\cdots \delta g^{kl}(x_n)}~. \end{aligned}$$

(34)

Now, when considering higher-point functions, the leading classical gravity approximation is valid when the underlying theory is string- or M-theory. Higher-order terms in the action will contribute corrections to the action, in the form of higher powers of the Riemann tensor and its derivatives, generically called ‘higher derivative terms’: see e.g. [14, Sect. 4.1.2] for a discussion. Nevertheless, though the techniques of Sect. 2 which rely on the definition of a Poincaré metric do not apply to the general case including the higher derivative terms, the concepts of visibility and invisibility do apply, for the higher-derivative terms in the action are covariant: and, in so far as $W_\mathrm{{QFT}}[g]$ is a functional of g only, the invisible diffeomorphisms will preserve the entire set of correlation functions (34).

The functional $W_\mathrm{{QFT}}[g]$ is of course only known for very specific QFTs, typically defined on a space which is close to flat or under specific assumptions about the topology of the conformal structure.¹⁸ In Appendix B, I calculate this functional exactly, in the important case of four-dimensional self-dual gravity metrics. From the bulk point of view, the renormalized stress-energy tensor has to be calculated solution by solution, through the near-boundary expansion, as mentioned.

The higher-point functions are harder to calculate: for we would need to know the variation of $g_{(d)}$ (in (33)) with respect to an arbitrary metric g, and, in the general case, this is beyond the reach of current techniques. However, we can compute it in specific cases, as I will illustrate in two examples, in Appendix B: of fluctuations around pure AdS, and of self-dual and massive gravity solutions.

In other words, checking that the correlation functions of the stress-energy tensor are indeed invisible to gravity-invisible diffeomorphisms requires the existence of a global solution: so that $g_{(d)}$ is indeed a functional of g. And, after all is said and done, the gravity-invisible diffeomorphisms defined in Sect. 2.2 do indeed come out as the correct QFT-invisible diffeomorphisms.

In the presence of matter in the bulk, the QFT at the fixed point has further operators, for instance $\langle T_{ij}(x_1)\,O(x_2)\rangle$, where $O(x_2)$ is a local operator which can be constructed out of new fields, and accordingly we get more states. I will comment on this case in Appendix C. For a review of dualities for gravity coupled to matter, see Skenderis [37].

3.2 Weakly Gravity-Visible Diffeomorphisms are QFT-Visible

In the previous subsection, and in Appendix B, we studied simply invisible diffeomorphisms in some detail, and concluded that they indeed preserve the physical quantities of the QFT. Now I will discuss how the weakly gravity-invisible diffeomorphisms found in Sect. 2 are seen by the QFT, hence are ‘QFT-visible’. By Propositions 1 and 2, weakly gravity-invisible diffeomorphisms give rise to a conformal, respectively Weyl, transformation of the representative of the boundary conformal structure g, as in (20). There are two ways in which these diffeomorphisms are indeed visible to the QFT.

The first way in which weakly-gravity invisible diffeomorphisms are visible to the QFT is their giving rise to conformal or Weyl transformations of the boundary QFT. More precisely, the boundary theory is a QFT at a conformally invariant fixed point, or a CFT. If the representative of the boundary conformal metric transforms under a weakly gravity-invisible diffeomorphism as $\varphi ^{-1}_M: g(x)\mapsto e^{-2\xi (x)}\,g(x)$ (see (19)), then transforming the other fields $\Phi _i(x)$ in the CFT (where i runs over the different species of fields) with specific weights $w_i\in \mathbb {R}$, $\Phi _i(x)\mapsto e^{w_i\,\xi (x)}\,\Phi _i(x)$, renders the theory (classically) invariant. But clearly, such a diffeomorphism is visible to the QFT: it is a conformal transformation of the fields.

There is a second way in which weakly-gravity invisible diffeomorphisms are visible to the QFT. Conformal transformations constitute a classical symmetry of the QFT at the fixed point but they are not always a symmetry of the quantum theory. There is a conformal anomaly for even values of the boundary dimension d Henningson and Skenderis [24].¹⁹ The gravity action is IR divergent due to the infinite volume of ${\hat{M}}$, as can be seen from the divergence of the Poincaré metric (2) at $r=0$, and so is renormalized in Eq. (32). Thus the action needs to be regularised, introducing a cutoff $r=\epsilon$, and renormalized [13, Sect. 3]. For even d, the renormalization procedure breaks the covariance of the action: one of the counterterms that are needed introduces a dependence of the classical action on the chosen representative of the boundary conformal structure. So, the classical action is anomalous under such transformations:

$$\begin{aligned} S_\mathrm{{ren}}[e^{-2\xi (x)}\,g]=S_\mathrm{{ren}}[g]+{{\mathcal {A}}}\,[g,\xi ], \end{aligned}$$

(35)

where ${{\mathcal {A}}}$ is the anomaly, which, for infinitesimal $\xi$, was computed in Henningson and Skenderis [24, Sect. 3]). Applying (33) and using the identification (32), it now follows that the stress-energy tensor transforms, under such diffeomorphisms, as:

$$\begin{aligned} \langle T_{ij}[e^{-2\xi (x)}\,g](x)\rangle =e^{(d-2)\,\xi (x)}\left( \langle T_{ij}[g](x)\rangle +{1\over \sqrt{g}}\,{\delta {{\mathcal {A}}}[g]\over \delta g^{ij}(x)}\right) . \end{aligned}$$

(36)

This transformation law can be found in De Haro et al. [13, Appendix C], for infinitesimal $\xi$. Of course, if we take the trace of (36), we reproduce the conformal anomaly, which was well-known in the conformal field theories in $d=2$, $d=4$, but had never been computed before in the $d=6$ theory that is dual to 7-dimensional Einstein gravity (see Deser and Schwimmer [16], Henningson and Skenderis [24, Sect. 3]: also De Haro et al. [14, Sect. 4.2.1]).

This shows that already the 1-point function of the stress-energy tensor exhibits anomalous behaviour under these diffeomorphisms, for even d: and, in this sense, the diffeomorphisms are visible and the theory is not conformally invariant. Notice that, in the QFT at the fixed point, this anomaly is a quantum effect, which is mirrored by the divergence of the classical gravity action.

4 Discussion and Conclusions

In this paper I have presented a number of results which: (i) make rigorous a number of physical intuitions about asymptotic symmetries in general relativity with a negative cosmological constant, and in gauge–gravity dualities; (ii) provide the mathematical and physical basis for the philosophical comparison of duality and gauge symmetry presented in De Haro et al. [14, Sects. 5, 6]); (iii) underpin the discussion of background-independence for gauge–gravity dualities in De Haro [11, Sects. 2.3.2–2.3.4].

These results are of physical interest in their own right. While the general gist of some of them may be known to experts in the conformal geometry of gauge–gravity duality, the mathematical and conceptual details are novel: and they bear on physical and philosophical discussions of general relativity and of duality.

As I have argued, the notion of weakly gravity-invisibility naturally makes precise the idea of asymptotic symmetries studied in the literature on general relativity and on gauge–gravity duality. These asymptotic symmetries are expected to induce the conformal transformations of the CFT. In this paper, weakly gravity-invisibility is defined as the preservation of appropriate structure, viz. the normal form of the metric and in addition either the boundary manifold M, in terms of its points (i.e. the diffeomorphism goes to the identity at infinity), or the representative of the conformal class g.

The first result was that weakly gravity-invisible diffeomorphisms give QFT-visible diffeomorphisms, namely, they indeed induce the conformal transformations of the CFT. Furthermore, the class of weakly gravity-invisible diffeomorphisms was shown to be larger than normally expected.

Secondly, the class of non-trivial strongly gravity-invisible diffeomorphisms was found to be empty: the only strongly gravity-invisible diffeomorphism is the identity. This is a surprising new result, because these diffeomorphisms were defined as preserving a very general, normal, form of the metric (a class of Poincaré metrics), while in addition preserving the conformal manifold M and the representative of the conformal class g.

Finally, the class of gravity-invisible diffeomorphisms turns out, as a consequence of the second point, smaller than expected. Nevertheless, non-trivial gravity-invisible diffeomorphisms do exist and are given by the diffeomorphisms satisfying both (ii) and (iii) in Sect. 2.2. There is of course no claim here that gravity-invisible diffeomorphisms exhaust the QFT-invisible diffeomorphisms: for there could be other diffeomorphisms that fit the bill.²⁰ The argument, in Sect. 3.1, that the gravity-invisible diffeomorphisms provide genuine QFT-invisible diffeomorphisms, in the sense that they do not act on the QFT, leaving all of its physical quantities unchanged, is rather non-trivial.

In the literature, the characterisation of the asymptotic symmetries is not always very precise. For instance, the class of non-trivial asymptotic symmetries—corresponding to my QFT-visible diffeomorphisms—is sometimes limited to only those diffeomorphisms which fix the radial direction r [28, Sect. 1.2]. But this is too restrictive: for, as we saw in Propositions 1 and 2 (see also the comment at the end of Sect. 2.2), the two classes of QFT-visible diffeomorphisms (those fixing (i) and (ii), and those fixing (i) and (iii)) have non-zero $\xi (x)$ (non-zero $\lambda (x)$, in the notation of the comment in Sect. 2.2), which parametrises the change of the radial coordinate: they act nontrivially along the r-direction while fixing $r=0$.

Also, it is sometimes claimed that the QFT-invisible diffeomorphisms are those that ‘go to unity at the boundary’ (this being the class by which the allowed diffeomorphisms have to be quotented in order to obtain the asymptotic symmetry group). But also this is imprecise: for a diffeomorphism can go to unity at the boundary (i.e. fixing (ii)) while still modifying the representative of the boundary conformal class through its r-dependence resulting in a rescaling of the metric $\xi (x)$, as shown in the proof of Proposition 2.

The correct QFT-invisibility condition to require is that the diffeomorphisms must fix both (ii) and (iii). Also, Theorem 3 ensures that the QFT-invisible diffeomorphisms form a class that is disjoint from the class of QFT-visible diffeomorphisms, i.e. the triviality of the class of diffeomorphisms fixing all of (i), (ii), (iii) means that the intersection between the QFT-visible and the QFT-invisible is empty. Thus in my construction there is no need to quotient the QFT-visible diffeomorphisms, as defined in Sect. 3.2, by that putative intersection.

The construction of a clear notion of QFT-invisible diffeomorphisms for general relativity and for gauge–gravity dualities carried out here, underlies the philosophical comparison in De Haro et al. [14, Sects. 2, 5, 6] between duality and gauge symmetry. More precisely, in that paper (Sect. 2) a distinction was made between: (i) gauge symmetries which are (Redundant), i.e. roughly: the formulation of the theory uses more variables than the number of degrees of freedom of the system being described; and (ii) gauge symmetries which are (Local), i.e. spacetime-dependent transformations. While the diffeomorphisms considered in this paper are all (Local) in this sense, not all of them are (Redundant).²¹

Let us now discuss which diffeomorphisms are (Redundant). The QFT-invisible diffeomorphisms are (Redundant): because the physical quantities do not depend on them.

On the other hand, the QFT-visible diffeomorphisms are potentially physical, in which case they cannot be (Redundant). In De Haro et al. [14, Sect. 6], the analogous case of Galileo’s ship thought experiment was used to illustrate how these diffeomorphisms, which are non-trivial at the boundary, can generate a relational physical difference between a proper subsystem and its environment when the action of the symmetry is restricted to the subsystem. Because of this characterization as a ‘subsystem’, these diffeomorphisms can indeed become physical. The condition for them to be physical can be cashed out in terms of what in De Haro [12, Sect. 1]²² is called an ‘external interpretation’. Such an external interpretation indeed treats the world described by the theory as a subsystem. On an external interpretation, then, QFT-visible diffeomorphisms are (Local) but not (Redundant).

But if an ‘internal interpretation’ is available: then, at least in the case of odd d—in which the conformal anomaly vanishes—the conformal symmetry might well be taken to be a redundancy of the theory’s formulation. Thus in this case the QFT-visible diffeomorphisms would become (Redundant). The conditions for an internal interpretation to obtain are spelled out in De Haro [12, Sect. 1].

Having specified the class of QFT-invisible diffeomorphisms, this can now be used to formulate a hole argument, labelled a ‘bulk’ argument, for Einstein spaces with a negative cosmological constant.

Most of the technical results presented in this paper rely only on the properties of the asymptotic behaviour of the Poincaré metric. Verifying that a diffeomorphism, for a given metric, is gravity-invisible involves just its asymptotic expansion. However, showing that the gravity-invisible diffeomorphisms are also QFT-invisible does involve assumptions about the global behaviour of the solutions, as we saw in Sect. 3.1 and, especially, in Appendix B: where QFT correlation functions were computed using global solutions.

Because the Fefferman–Graham expansion (30) turns the problem of solving a differential equation asymptotically into that of solving a set of coupled algebraic relations, the results that only depend on the asymptotic solutions can be analytically continued: from the case of a negative cosmological constant or AdS, to the case of a positive cosmological constant, or de Sitter space, $\ell _\mathrm{{AdS}}\mapsto i\ell _\mathrm{{dS}}$.²³ Indeed, the bulk hole argument of De Haro et al. [14, Sect. 6] only strictly requires an infinitesimal neighbourhood of the boundary. Hence the gravity-invisible diffeomorphisms defined here can be used to make a bulk/hole argument for (generalised) de Sitter space, where the anti-de Sitter boundary is mapped to timelike future infinity in de Sitter space.

But the methods developed here, of constructing diffeomorphisms that preserve the relevant asymptotic structures, should readily generalize to cases in which there is no Fefferman–Graham structure like Eqs. (2) and (30) but instead some other kind of asymptotic expansion. For one such class of examples, in which the QFT is a non-relativistic quantum field theory, i.e. the spacetime has a globally defined time coordinate and a preferred foliation, see Janiszewski and Karch [28, Sect. 1.2]. In such a case, the QFT-visible diffeomorphisms should be the ones that preserve the corresponding structure, and which at the boundary induce the symmetries of the non-relativistic QFT.

The distinction between QFT-visible versus invisible diffeomorphisms establishes the two relevant kinds of diffeomorphisms which were discussed in detail in De Haro [11, Sect. 2.3.3], and to which two kinds of analyses of background-independence applied. These two kinds of diffeomorphisms taken together formed what in that paper were called diffeomorphisms that ‘preserve the asymptotic form of the metric’ (labelled (a1)). In this paper I have thus specified that the metric structure preserved can be either: (b: QFT-visible) the normal form of the metric and in addition M or g; (c: QFT-invisible) M and g. The mathematical details of the discussion [11, Sect. 2.3.3] of the (lack of) covariance of the physical quantities for the QFT-visible diffeomorphisms, for even values of d, have now been fleshed out in Sect. 3.2, and in particular the anomalous transformation is in Eq. (36). In De Haro [11, Sect. 2.3.3], the two kinds of diffeomorphisms (a1) discussed here were distinguished from yet another class, labelled (a2), of ‘large’ diffeomorphisms: which do not preserve any of the pairwise structures (a)–(c) considered in the Introduction. These diffeomorphisms are expected to map solutions to inequivalent solutions. It would be interesting to investigate this class of diffeomorphisms.

These results also make it possible to now discuss the important philosophical question of the possible emergence of diffeomorphism invariance.

Appendices

Appendix A: A Condition for Gravity-Invisibility

At the end of Sect. 2.4, I discussed an alternative definition the induced metric $\gamma _{\mu \nu }$, which is common in general relativity. In this appendix I compute the induced metric and show that it gives the same conditions for invisibility.

The normal covector to the boundary $r=0$, $n={\ell \over r}\,\text{ d }r$, transforms as:

$$\begin{aligned} \phi ^*n= & {} {\ell \over \tilde{r}}\left( \left( 1-\partial _{\tilde{r}}\xi (\tilde{x},\tilde{r})+{1\over \tilde{r}}\,\xi (\tilde{x},\tilde{r})\right) \text{ d }r-\partial _i\xi (\tilde{x}, \tilde{r})\,\text{ d }x^i\right) ~. \end{aligned}$$

(37)

The induced metric on the boundary is: $\gamma _{\mu \nu }:=g_{\mu \nu }-n_\mu n_\nu$, so that it transforms as:

$$\begin{aligned} (\phi ^*\gamma )_{ij}= & {} {\ell ^2\over \tilde{r}^2}\left( \left( 1+\xi (\tilde{x},\tilde{r})\left( {2\over \tilde{r}}-\,\partial _{\tilde{r}}\right) \right) g_{ij}(\tilde{x},\tilde{r})+\nabla _i\xi _j+\nabla _j\xi _i\right) \nonumber \\ (\phi ^*\gamma )_{ir}= & {} {\ell ^2\over \tilde{r}^2}~g_{ij}(\tilde{x},\tilde{r})~\partial _{\tilde{r}}\xi ^j(\tilde{x},\tilde{r})\nonumber \\ (\phi ^*\gamma )_{rr}= & {} 0 \end{aligned}$$

(38)

Let us define the transformed metric ${\hat{h}}:=\phi ^*\gamma =:{\ell ^2\over r^2}\,h$, then the conformal metric is $h={r^2\over \ell ^2}\,\phi ^*\gamma$. Its components are:

$$\begin{aligned} h_{ij}= & {} \left( 1-\xi (\tilde{x},\tilde{r})\,\partial _{\tilde{r}}\right) g_{ij}(\tilde{x},\tilde{r})+\nabla _i\,\xi _j(\tilde{x},\tilde{r})+\nabla _j\,\xi _i(\tilde{x},\tilde{r})\nonumber \\ h_{ir}= & {} g_{ij}(\tilde{x},\tilde{r})~\partial _{\tilde{r}}\xi ^j(\tilde{x},\tilde{r})~. \end{aligned}$$

(39)

Since $\gamma$ is the metric normal to the vector $n^\mu$, whose components are tangential to the boundary, the criterion for QFT-invisibility is that $\phi$ leaves this metric unmodified. We will now calculate whether, for specific values of $\alpha$ and $\beta$ above, there are any obstructions for the existence of invisible diffeomorphisms. As before, we set $\xi (\tilde{x},\tilde{r})=\tilde{r}^\alpha \,\xi (\tilde{x})$, $\xi ^i(\tilde{x},\tilde{r})=\tilde{r}^\beta \,\xi ^i(\tilde{x})$.

For $\beta \ge 2$, we get $h_{ij}|_{\tilde{r}=0}=g_{ij}$ and $h_{ir}|_{\tilde{r}=0}=0$ and such a diffeomorphism is invisible.

For $\beta =1$, the components along the boundary are still unaffected, but $h_{ir}|_{\tilde{r}=0}=\xi _i$ and the diffeomorphism is visible, like before.

For $\beta =0$, we get $h_{ir}|_{\tilde{r}=0}=0$ identically. But the diffeomorphism has a visible effect: it generates non-zero $h_{ij}|_{\tilde{r}=0}=\nabla _i\xi _j+\nabla _j\xi _i$, as before.

Appendix B: QFT Correlation Functions: Three Examples

In this Appendix, I will calculate the correlation functions (34) in three examples of bulk solutions, which will exhibit explicitly the dependence between $g_{(d)}$ and g, discussed in §3.1. The aim is to show the independence of the QFT quantities (34) from the gravity-invisible diffeomorphisms, thus illustrating the general point made in §3.1. These examples thus show that the mathematical theory developed in Sect. 2 is relevant in the important physical sense of being instantiated in non-trivial examples of gauge–gravity dualities.

I will consider solutions with Euclidean signature and $d=3$, i.e. solutions of a four-dimensional, Euclidean theory in the bulk.

1.1 Appendix B.1: Perturbations of a Flat Boundary

Consider a representative of the boundary conformal structure that is almost flat,

$$\begin{aligned} g_{ij}(x,r)=\delta _{ij}+h_{ij}(r,x), \end{aligned}$$

(40)

where $h_{ij}$ is the linealised fluctuation around the Euclidean solution. It is not hard to show that Einstein’s equations have a unique regular, linearized solution, which can be written entirely in terms of the transverse, traceless part of $h_{ij}(r,x)$. (The solution is in Sect. 2 of De Haro [10]). This solution then has itself an expansion in r, the coefficients of which satisfy:

$$\begin{aligned} \bar{h}_{(3)}={1\over 3}\,|\Box |^{3/2}\,\bar{h}_{(0)}, \end{aligned}$$

(41)

where $\bar{h}$ denotes the transverse, traceless part of h, obtained by projecting: $\bar{h}_{ij}=\Pi _{ijkl}\, h_{kl}$. Substituting this into (33) thus gives the 1-point function of the stress-energy tensor, and the two-point function is obtained by a further variation (in momentum space):

$$\begin{aligned} \langle T_{ij}T_{kl}\rangle ={\ell ^2\over 8\pi G_\mathrm{{N}}}\,|p|^3\,\Pi _{ijkl}~. \end{aligned}$$

(42)

This two-point function is indeed invariant under gravity-invisible transformations. In this particular case, all the higher-point functions vanish.

1.2 Appendix B.2: Self-dual Solutions

Another case of interest is that of bulk solutions for which the Weyl tensor is self-dual:

$$\begin{aligned} C_{\mu \nu \alpha \beta }={1\over 2}\,\,\epsilon _{\mu \nu \lambda \sigma }\,C_{\alpha \beta }{}^{\lambda \sigma }, \end{aligned}$$

(43)

and in the anti-self-dual case there is a relative minus sign. These solutions have a $g_{(3)}$, i.e. a boundary condition which equals the Cotton tensor $C_{ij}$ (De Haro [10]), and so the stress-energy tensor is:

$$\begin{aligned} \langle T_{ij}\rangle ={\ell ^2\over 8\pi G_\mathrm{{N}}}\,C_{ij}[g], \end{aligned}$$

(44)

where the two-index Cotton tensor is a traceless and conserved 2-tensor,²⁴ given by:

$$\begin{aligned} C_{ij}:={1\over 2}\,\,\epsilon _i{}^{kl}\,\nabla _k\left( R_{jl}-{1\over 4}\,g_{jl}\,R\right) ~. \end{aligned}$$

(45)

I emphasize that the stress-energy tensor (44) is exact: there is no linearization involved. The bulk solutions satisfying (43) are usually called gravitational instantons. Because the result (44) is exact, we can (very exceptionally!) calculate the exact generating functional, up to a constant. It is given by the gravitational Chern-Simons action:

$$\begin{aligned} W_\mathrm{{QFT}}=-{\ell ^2\over 32\pi G_\mathrm{{N}}}\,\int \mathrm{Tr}\left( \Gamma \wedge \text{ d }\Gamma +{2\over 3}\,\Gamma \wedge \Gamma \wedge \Gamma \right) , \end{aligned}$$

(46)

and an anti-self-dual solution has a plus sign. Furthermore, we can calculate from (44) all the higher-point functions (34) in the QFT, which correspond to self-dual solutions (43).

For instance, take a squashed 3-sphere, with metric:

$$\begin{aligned} g= & {} {\ell ^2\over 4}\left( \sigma _1^2+\sigma _2^2+\alpha \,\sigma _3^2\right) \nonumber \\ \sigma _1+i\sigma _2= & {} e^{-i\psi }\left( \text{ d }\theta +i\,\sin \theta \,\text{ d }\varphi \right) \nonumber \\ \sigma _3= & {} \text{ d }\psi +\cos \theta \,\text{ d }\varphi , \end{aligned}$$

(47)

where $\alpha$ is the squashing parameter. The round three-sphere is obtained when $\alpha =1$, and the scalar curvature is $R={8\over \ell ^2}\left( 1-{\alpha \over 4}\right)$. As a function of the metric, the Cotton tensor is then given by the following identity: ${\text{ Ric }}-{1\over 3}\,R\,g+{\ell \over 3\sqrt{\alpha }}\,C=0$. Explicitly, it takes the following form:

$$\begin{aligned} C={1\over \ell }\left( \alpha -1\right) \sqrt{\alpha }\left( \sigma _1^2+\sigma _2^2-2\alpha \,\sigma _3^2\right) . \end{aligned}$$

(48)

Of course, for a round three-sphere, i.e. $\alpha =1$, the Cotton tensor vanishes.

The mathematical interest in these solutions goes back to Pedersen and LeBrun..., but was revived by the Fefferman–Graham results in Anderson... For some examples of gravitational instantons, see e.g. Martelli et al. [30].

1.3 Appendix B.3: Topologically Massive Gravity

The previous kind of solution can be generalised to so-called topologically massive gravity theories in three dimensions. The starting point of the generalization is to include, in the boundary condition, in addition to the Cotton tensor, a Ricci term:

$$\begin{aligned} {3\ell ^2\over \,32\pi G_\mathrm{{N}}}~g_{(3)}=\mu \,{\text{ Ric }}[g]-C[g], \end{aligned}$$

(49)

where $\mu$ is the mass introduced, on dimensional grounds, by the boundary condition. Again, for such solutions the all-order (34) can be computed. At the linearized level, the 2-point function is:

$$\begin{aligned} \langle T_{ij}T_{kl}\rangle ={\ell ^2\over 8\pi G_\mathrm{{N}}}\,|p|^3\,\Pi _{ijkl}+{ip^2\over \mu }\,\epsilon _{imp}\,p_n\,\Pi _{jmkl}~. \end{aligned}$$

(50)

To conclude this Appendix: As claimed, these examples illustrate how: (i) the higher-point functions, which are the quantities of interest in the theory, can be calculated, and (ii) that they are invariant under invisible diffeomorphisms as defined in §2.4. Thus, the mathematical theory here developed is physically, as well as mathematically, non-empty.

Appendix C: Coupling Gravity to Matter

Showing that the methods of Fefferman and Graham generalise to theories with matter was the topic of Sect. 5 in De Haro et al. [13]. In the same way that Poincaré metrics can be constructed with given boundary conformal data, matter fields (such as scalar fields satisfying the Klein-Gordon equation, or gauge fields satisfying their equation of motion) can be solved for by using similar methods, i.e. solving an asymptotic series given boundary conditions on M. A similar structure arises, with the expectation values of an operator $\langle O_\Delta (x)\rangle$ of scaling dimension $\Delta$ being given by the 1-point functions of the canonical momenta associated to bulk matter. Of course, now one has to solve the coupled gravity-matter equations: but this can be done asymptotically: and for fields within the unitarity bounds of the dual QFTs, the Fefferman–Graham expansion works. For illustration, the one-point function dual to a scalar field of mass m is given by:

$$\begin{aligned} \langle O_{\Delta _+}(x)\rangle =\left( 2\Delta _+-d\right) \phi _{(2\Delta _+-d)}+(\text{ local } \text{ terms }), \end{aligned}$$

(51)

where $\Delta _+$ the dimension of the operator and $\phi _{2(\Delta _+-d)}$ is the coefficient in the Fefferman–Graham expansion at order $\Delta _+$:

$$\begin{aligned} \phi (x,r)=r^{\Delta _-}\left( \phi _{(0)}(x)+r\,\phi _{(1)}(x) +\cdots +r^{\Delta _+-\Delta _-}\,\phi _{(2\Delta _+-d)}\right) , \end{aligned}$$

(52)

where $\Delta _\pm :={d\over 2}\pm \sqrt{{d^2\over 4}+m^2\ell ^2}$. $\Delta _+$ is the scaling dimension of the operator O(x) in the QFT.

Now if the dimensions of operators that we add to the QFT are within the unitarity bounds, the back-reaction of the fields on the metric does not affect its leading behaviour [13, Sect. 5.2]. So, although the technical details in the derivation of the invisible diffeomorphisms in Sect. 2 will differ, the conclusion (c), in Sect. 1, that there is a non-empty class of such diffeomorphisms will be unaffected, and therefore the invisibility analysis in Sect. 3 is not affected by the addition of matter.