Abstract
In an accompanying paper Gomes (arXiv:1504.02818, 2015), we have put forward an interpretation of quantum mechanics based on a non-relativistic, Lagrangian 3+1 formalism of a closed Universe M, existing on timeless configuration space \(\mathcal {Q}\) of some field over M. However, not much was said there about the role of locality, which was not assumed. This paper is an attempt to fill that gap. Locality in full can only emerge dynamically, and is not postulated. This new understanding of locality is based solely on the properties of extremal paths in configuration space. I do not demand locality from the start, as it is usually done, but showed conditions under which certain systems exhibit it spontaneously. In this way we recover semi-classical local behavior when regions dynamically decouple from each other, a notion more appropriate for extension into quantum mechanics. The dynamics of a sub-region O within the closed manifold M is independent of its complement, \(M-O\), if the projection of extremal curves on \(\mathcal {Q}\) onto the space of extremal curves intrinsic to O is a surjective map. This roughly corresponds to \(e^{i\hat{H}t}\circ \mathsf {pr}_{\mathrm{O}}= \mathsf {pr}_{\mathrm{O}}\circ e^{i\hat{H}t}\), where \(\mathsf {pr}_{\mathrm{O}}:\mathcal {Q}\rightarrow \mathcal {Q}_O^{\partial O}\) is a linear projection. This criterion for locality can be made approximate—an impossible feat had it been already postulated—and it can be applied for theories which do not have hyperbolic equations of motion, and/or no fixed causal structure. When two regions are mutually independent according to the criterion proposed here, the semi-classical path integral kernel factorizes, showing cluster decomposition which is the ultimate aim of a definition of locality.


Similar content being viewed by others
Notes
While it is true that one can extend phase space to include so-called “embedding variables”, for which one can better represent the spacetime diffeomorphisms canonically [5], but these require further gauge-fixing and the complication of more fields, and it is not clear to me that they fully alleviate the problem.
See[6] for conditions under which we can extend these usual theorems to the infinite dimensional Banach context.
I will not discuss much how this surface would be determined under practical circumstances. One could say it is defined locally in \(\mathcal {Q}\) by a radius of length \(r_o\) (according to some local scale) from a given preferred point \(x_o\), but then one would have to determine how this point is defined and so on. Suffice it to say here that an observer (whatever that means) can ascertain that there is a region (diffeomorphic) to \(S^2\) where the fields stay approximately constant so far as the observer can tell.
We should have written \(\partial \overline{O}\), where the over bar is the closure, but we avoid it in order to not clutter notation and not to confuse it with \(\bar{g}_{ab}\), where the bar has nothing to do with closure of course. Moreover, note that we are abusing the restriction notation \(A_{|O}\), in identifying it with the intrinsic induced metric (not merely the full metric restricted to those base points).
Given the characteristic function \(\chi _A\) valued in \(\{0,1\}\), whose value is: \( \Theta _A(x)= \left\{ \begin{array}{rl} 1 &{}\, ~\text{ if }\, ~x\in A\\ 0 &{}\, ~\text{ if }\, ~x\notin A \end{array}\right. \), we have that the metric is given by \( g_{ab}(x):=g_{ab}(x)\Theta _O(x)+g_{ab}(x)\Theta _{O^C}(x)\). To actually have the embedding explicitly, one could use the regular value theorem with projection from \(\mathcal {Q}\) to \(\mathcal {Q}_O\), with such characteristic functions.
The same would occur if we were to consider Weyl transformations of the metric, since they also act locally and intrinsically on the metric, forming an equivalence relation.
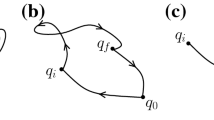
Note however, that since in the present ‘‘many-worlds’’ type of view, there isn’t a single history of the Universe, and there can be interference among distinct paths in configuration space. Thus this notion that EPR pairs are correlated in each path in configuration space does not contradict Bell’s theorem.
In this case, upon an infinite expansion of the inverse Laplacian operator, we would have to add an infinite expansion of derivatives of \(\phi \) on the boundary, which is in accord with the theory being non-local.
But are not necessarily in \(\mathcal {Q}^{\partial O}_M\), i.e. not necessarily maintaining the boundary conditions throughout.
Although there are arguments for the existence and uniqueness of solutions of the gravitational dynamics for GR (see [17, ch 7]), they are predicated on minimum levels of differentiability of sources and fields (as extensions of the analytic case). However, this excludes the use of Dirac-deltas and Heaviside functions, used in potential walls and double-slits for example. As Marsden has shown [18], using such sources can elicit mulitplicity of solutions.
This is a more space-time-framed version of the dynamical point of view, in which the overall extremal curve doesn’t reduce to the local (intrinsic) extremal curve.
This is known as the ‘near-zone’ fields. In the case of electromagnetism, one can look at the propagation of effects of perturbations caused by charge acceleration in the Lienard-Wiechart potential (by discarding the advanced solutions), and indeed, these propagate at the speed of light. But there is some difficulty in distinguishing the near-zone effects from the wave-zone effects, especially once one takes into account quantum mechanics (see [24, Chapter 7], and references therein). But even this point is not as trivial in the gravitational case, as the wave equation is already for a perturbation in the field.
It could still be true however that these constants don’t match for different regions \(\mathcal {U}\) where semi-classical decoupling is valid. This is not a big problem however, because the product formula is in any case only shown to hold separately for each of these particular regions.
It is also important to note that Definition 1 goes beyond the demand, in Hamiltonian mechanics, that the dynamics preserve the submanifolds defined by the region. That is because we want to say that the region has an intrinsically defined dynamics, which must match, and be given by, the projection of the Hamiltonian flow. More effort needs to be put into the translation of these concepts to the Hamiltonian (symplectic geometry) setting.
If no factorization is exact, i.e. if the higher momentum modes couple in a non-trivial way to the lower momentum ones, one could perhaps detect the presence of a fundamental high momentum cuttoff from interference effects of the lower momentum ones.
Note that it is difficult to tell whether an action is local or not by just looking at its Lagrangian. That is, it might be local in some gauge, while not in others. And looking at observables doesn’t really help, as in gravitational theories they are almost certainly non-local.
Where entanglement entropy usually can diverge, for example.
For classical non-relativistic particle mechanics, one could have that \(V>E\), in which case one would obtain a purely imaginary action from the Jacobi procedure. This is related to the phenomenon of tunneling, which can be represented either as solutions of the Euclidean action (instantons) or from imaginary valued solutions of the equations of motion [35] in real time. See also [36] for a way to obtain tunneling phenomena from the real-time path integral.
In a finite-dimensional dynamical system of dimension d, this takes the form of the phase space volume occupied by a quantum state: \(A=(2\pi \hbar )^{-d}\).
References
Gomes, H.: Back to parmenides. In: Winner of the “Space-Time After Quantum Gravity” Essay Contest (2016)
Koslowski, T.A.: Shape dynamics and effective field theory. Int. J. Mod. Phys. A28, 1330017 (2013)
Gomes, H.: Path integrals in configuration space and the emergence of classical behavior for closed systems. arXiv:1504.02818 (2015)
Gomes, H.A.: A geodesic model in conformal superspace. arXiv:1603.01569 (2016)
Isham, C., Kuchar, K.: Representations of spacetime diffeomorphisms. II. Canonical geometrodynamics. Ann. Phys. 164(2), 316–333 (1985)
Kriegl, A., Michor, P.W.: The Convenient Setting of Global Analysis. American Mathematical Society, Providence, RI (1997)
Freed, D.S., Groisser, D.: The basic geometry of the manifold of Riemannian metrics and of its quotient by the diffeomorphism group. Mich. Math. J. 36(3), 323–344 (1989)
Fischer, A.R.: The theory of superspace. In: M. Carmeli, S.I. Fickler, L. Witten (eds.) Proceedings of the Relativity Conference held 2-6 June, 1969 in Cincinnati, OH, p. 303. Plenum Press, New York (1970)
Giulini, D.: What is the geometry of superspace? Phys. Rev. D 51, 5630–5635 (1995)
Gilbarg, D., Trudinger, N.: Elliptic partial differential equations of second order. Springer, New York (2001)
Gil-Medrano, O., Michor, P.W.: The riemannian manifold of all riemannian metrics. Q. J. Math. 42, 183–202 (1991)
Lee, J., Wald, R.M.: Local symmetries and constraints. J. Math. Phys. 31(3), 725–743 (1990)
Arnowitt, R., Deser, S., Misner, C.: The dynamics of general relativity. In: Witten, L. (ed.) Gravitation: an introduction to current research, pp. 227–264. Wiley, New York (1962)
Gomes, H., Gryb, S., Koslowski, T.: Einstein gravity as a 3D conformally invariant theory. Class. Quant. Grav. 28, 045005 (2011)
Schroedinger, E.: Die gegenwartige situation in der quantenmechanik. Naturwissenschaften 23(48), 807–812 (1935)
Regge, T., Teitelboim, C.: Role of surface integrals in the hamiltonian formulation of general relativity. Ann. Phys. 88, 286–318 (1974)
GFRHS, Ellis: The Large Scale Structure of Space-Time. Cambridge University Press, New York (1973)
Marsden, J.: Generalized hamiltonian mechanics a mathematical exposition of non-smooth dynamical systems and classical hamiltonian mechanics. Archive for rational mechanics and analysis 28(5), 323–361 (1968)
Gomes, H. Riello, A.: The observer’s ghost: a field-space connection-form and its application to gauge theories and general relativity. arXiv:1608.08226 (2016)
Gomes, H.: Gauge theory in riem: classical. J. Math. Phys. 52, 082501 (2011)
Gourgoulhon, E.: 3+1 formalism and bases of numerical relativity. In: Lecture notes in Physics 846. Springer, New York (2007)
Maxwell, D.: The conformal method and the conformal thin-sandwich method are the same. Class. Quant. Grav. 31, 145006 (2014)
Mercati, F.: A shape dynamics tutorial. arXiv:1409.0105 (2014)
Strocchi, F.: An Introduction to Non-perturbative Foundations of Quantum Field Theory. Oxford University Press, Oxford (2013)
Johnson, D., Whitt, L.: Tottaly geodesic foliations. J. Differ. Geom. 15, 225–235 (1980)
Reuter, M.: Nonperturbative evolution equation for quantum gravity. Phys. Rev. D 57, 971–985 (1998)
Horava, P.: Quantum gravity at a Lifshitz point. Phys. Rev. D 79, 084008 (2009)
Eling, C., Jacobson, T., Mattingly, D.: Einstein-aether theory. pp. 163–179. arXiv:gr-qc/0410001 (2004)
Page, D.N.: Clock time and entropy. In: NATO Workshop on the Physical Origin of Time Asymmetry Mazagon, Spain, September 30-October 4, 1991, pp. 0287–298 (1993)
Barbour, J.: The End of Time: The Next Revolution in Physics. Oxford University Press, Oxford (1999)
Gomes, H.: Quantum gravity and the timeless path integral. To appear
Bianchi, E., Hackl, L., Yokomizo, N.: Entanglement time in the primordial universe. Int. J. Mod. Phys. D 24(12), 1544006 (2015)
Ebin, D.: The manifold of riemmanian metrics. In: Proceedings of Symposia in Pure Mathematics, AMS, vol. 11, 15 (1970)
Palais, R.: On the existence of slices for the actions of non-compact groups. Ann. Math. 73, 295–322 (1961)
Turok, N.: On quantum tunneling in real time. N. J. Phys. 16, 063006 (2014)
Tanizaki, Y., Koike, T.: Real-time feynman path integral with picard lefschetz theory and its applications to quantum tunneling. Ann. Phys. 351, 250–274 (2014)
Acknowledgements
I would like to thank Clement Delcamp for drawing the figures. This research was supported by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 A.1 Principal Fiber Bundles
Principal fiber bundles are useful in the discussion of symmetry groups.
A principal fiber bundle is a manifold P, on which a Lie group G acts freely: \(P\times G\rightarrow P\), here we will assume it acts on the left, \((p, g)\rightarrow g\cdot p=L_g(p)\). The space \(\{g\cdot p\,~|~g\in G\}\) is called the the fiber (through p). Identifying \(p\sim g\cdot p\), we have a projection operator onto the quotient space \(\pi : P\rightarrow P/G\). We will use the square bracket notation to denote the orbit of p, i.e. \([p]=\pi ^{-1}(\pi (p))\subset P\), but since there is a one to one correspondence between orbits and points in P / G, we sometimes abuse notation and write \([p]=\pi (p)\in P/G\).
For some open region \(U\in P/G\), with the use of a section \(\chi :U\rightarrow P\), we can trivialize the bundle: \(\pi ^{-1}(U)\simeq \chi (U)\times G\), which allows us to write \(P\ni p= (x\,,\, g)\) for \(x\in U\). Sections intersect each orbit of the gauge group only once. Given two sections, they are always uniquely related by a function \(\lambda :U\rightarrow G\), as in \(\chi _1(x)= \lambda (x)\cdot \chi _2(x)\).
Given \(\mathfrak {v}\in \mathfrak {g}\), where \(\mathfrak {g}:=T_{ \text{ Id }}G\), we define the fundamental vector field associated to it as \(T_pP\ni \mathfrak {v}_p^\#:=\frac{d}{dt}_{|t=0}\exp {(t\mathfrak {v})}\cdot p\). The vertical subspace \(V_p\subset T_pP\) is the tangent space to the fiber at p, i.e. \(V_p=\text{ span }\{\mathfrak {v}_p^\#\,~|~\mathfrak {v}\in \mathfrak {g}\}\).
In standard gauge field theory, the space of physically equivalent field configurations requires that one quotient the total space of field configurations by the total group of gauge transformations, \(\mathcal {A}/\)Gau(G), where \(\mathcal {A}\) is the field space of connections on space-time, G is the internal symmetry group and Gau(G) is the group of space-time dependent gauge-transformations. A choice of gauge is a smooth embedding
such that each orbit only intersects the image of \(\chi \) once, and it does so transversally, i.e. \(\text{ Im }(T_A\chi )\oplus V_A=T_A\mathcal {A}\).
Usually, due for instance to Gribov ambiguities, there is no global section \(\chi \), and we need to restrict the section to an open set,
where \(\pi :\mathcal {A}\rightarrow \mathcal {A}/\text{ Gau }(G)\) is the projection operator onto the quotient space and \(\mathcal {U}\) is some open region in \(\mathcal {A}\).
1.2 A.2 Slice Theorem for Riem
Ebin and Palais have shown that \(\mathcal {Q}\) has a local slice [33, 34]. They did this through the use of the normal exponential map to the orbit along a given point. That is, for an arbitrary given metric \(\bar{g}_{ab}\), the orbits were shown to be embedded manifolds, and the normal exponential (according to the supermetric (3) with \(\lambda =0\)): \(\text{ Exp }_{\bar{g}}:W\subset V_{\bar{g}}^\perp \rightarrow \mathcal {Q}\) was shown to be a local diffeomorphism onto its image for a given open set W, where, as can easily be seen from the form of \(V_g\) and (3),
By then showing that the tubular bundle around this orbit was locally diffeomorphic to \(\mathcal {Q}\), one has, for \(g_{ab}\in \pi ^{-1}(\pi (\text{ Im }(\text{ Exp }_{\bar{g}}(W)))\), a unique \(f_g\in \text{ Diff }(M)\) such that
for a unique \(w_g\in W\),
Thus
Furthermore, for \(g^2_{ab}=h^*g^1_{ab}\), we then have \(f_{g^2}=h^{-1}\circ f_{g^1}\). Thus \(w_g=w_{[g]}\) and for any \(\tilde{g}_{ab}\in [g_{ab}]\subset \pi ^{-1}\pi (\mathcal {U})\), the section is given by
In more heuristic terms, \(\chi \) takes any metric along the orbits and translates it along the orbit until it hits the orthogonal exponential section at the height of \(\bar{g}_{ab}\). This intersection gives us the value of \(\chi \) for the given equivalence class.
Another way of saying it would be to use the ‘best-matching’ ideas (see e.g. [23]). In this context, the choice of representative of a metric would be the one that requires the ‘least’ deformation to get to your metric (where ‘least’ is wrt some supermetric in Riem).
1.3 A.3 The Jacobi Metric
The Jacobi version of the Maupertuis principle establishes some instances when dynamics can be viewed as geodesic motion in an associated Riemannian manifold. That is, if the action can be written as
for a system defined in a Riemannian manifold, (M, g), with smooth potential U, the extremal trajectories of S with energy \(E = T + U\) coincide with the extremals (geodesics) of the length functional
defined in (M, h), where h is the Jacobi metric, conformally related to g by \(h = 2(E - V)g\). This I will call the Jacobi procedure, whereby one builds a metric in configuration space whose geodesics are extremal paths of the action.Footnote 18
1.4 A.4 The Semi-classical Approximation
Given an action S in the configuration space of some field \(\phi \) over a spatial manifold M, one can build the path integral propagator between an initial and final configuration, \(\phi _1\) and \(\phi _2\) as:
where \(\Gamma (\phi _1,\phi _2)\) is taken to be the space of paths (in some differentiability class) between \(\phi _1\) and \(\phi _2\), and I used square brackets to denote functional dependence.
The following semi-classical, or saddle point, approximation for the path integral in configuration space was the fundamental object used in [3]. For (locally) extremal paths \(\gamma _{\text{ cl }}\) between an initial and a final field configuration, denoting the on-shell action for these paths as \(S_{\gamma _{\text{ cl }}}\), accurate for \(1<< S_{\gamma _{\text{ cl }}}/\hbar \), it can be written as:
where A is a normalization factor (independent of the initial and final configurations),Footnote 19 I used square brackets to denote functional dependence of the on-shell action, and the Van Vleck determinant is now defined as
where we used DeWitt’s mixed functional/local dependence notation \([{\phi ^*}; x)\), and the on-shell momenta is defined as
The Van-Vleck matrix is degenerate when gauge-symmetries exist, in which case one must provide a suitable gauge-fixing. If it is not degenerate, it embodies the spread of classical trajectories.
Rights and permissions
About this article
Cite this article
Gomes, H. Semi-classical Locality for the Non-relativistic Path Integral in Configuration Space. Found Phys 47, 1155–1184 (2017). https://doi.org/10.1007/s10701-017-0105-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-017-0105-4