Abstract
The simple concept of a SIC poses a very deep problem in algebraic number theory, as soon as the dimension of Hilbert space exceeds three. A detailed description of the simplest possible example is given.
Similar content being viewed by others
1 Introduction to the SIC Existence Problem
Physicists rarely care about numbers; that is to say, they rarely care about the nature of numbers. Indeed, they routinely and unquestioningly rely on the real number system. Still, doubts are sometimes expressed. Thus, Schrödinger referred to quantum mechanics as a “makeshift”, because it seemingly does not at all challenge the notion of the continuum [1]. Be that as it may, there is an easily formulated quantum mechanical question forcing us to come directly to grips with a major unsolved problem concerning numbers.
The question arose very naturally in the context of quantum state tomography, where an informationally complete and symmetric POVM would be a desirable thing to have [2], and even earlier from a highly original mathematical perspective on quantum theory [3]. It also appears in classical signal processing; in fact there is an engineering side of the question, although why this is so will not be made evident here. The question is: in a complex Hilbert space of d dimensions, can one find \(d^2\) vectors \(|\psi _I\rangle \) such that
Such a collection of vectors, if it exists, is known as a SIC [4]. SICs are also known as maximal equiangular tight frames, as minimal complex projective 2-designs, and—no doubt—under many other names.
Numbers can be added and multiplied to form new numbers. Indeed they form sets, known as fields, that are closed under addition, subtraction, multiplication, and division. A standard example is the field of rational numbers \(\mathbf{Q}\), which is generated from the integers by applying the field operations. Every field having an infinite number of elements contains \(\mathbf{Q}\) as a subfield. Examples include the real number field \(\mathbf{R}\) (against which Schrödinger expressed his reservations) and the complex number field \(\mathbf{C}\). The ancient Greeks (in particular, Eudoxos) gave a definition of the real numbers, but they also payed particular attention to a smaller extension of \(\mathbf{Q}\), consisting of numbers that can be geometrically constructed using ruler and compass. Algebraically this corresponds to the requirement that all the numbers that occur are given in terms of nested square roots of rational numbers. This number field turned out to be too small for some purposes, for instance one needs the cube root \(\root 3 \of {2}\) in order to duplicate the cube. More generally we can consider fields built using nested radicals, including cube roots, quartic roots, and so on. During the Italian Renaissance there was a race to express the solutions of polynomial equations in terms of radicals, but it was eventually shown by Abel and Galois that this is not possible in general. The lesson learned from this brief excursion into history is that the choice of the number field depends on the particular task one is facing.
The question is: what number field is needed to construct SICs? A conjectural, but precise and highly remarkable, answer is now available [5]. Our purpose here is to describe this answer using the simplest non-trivial example, where almost all the calculations can be done with pencil and paper.
2 Introducing the Weyl–Heisenberg Group
If \(d = 2\) the SIC existence question is trivial. Moreover, the vectors being sought are then always fully determined by a complete set of mutually unbiased bases, in a geometrically natural way. Although it is considerably harder to see (one will have to read several papers in order to patch a proof together [6,7,8,9]), this statement holds also when \(d = 3\). Numerically, SICs have been found in every dimension where they have been looked for (this includes all dimensions \(d \le 121\), and a few more [10, 11]), but no existence proof has been found, and beyond three dimensions it is very hard to see an underlying pattern in the solutions. Yet closer inspection reveals that there is a pattern also when \(d \ge 4\). This pattern, so far as it is understood, resides in number theoretical properties of exact solutions for SICs [5, 12], and the simplest non–trivial example occurs when \(d = 4\).
To see how exact solutions can be obtained, we first take note of the fact that all known SICs (with one exception) form orbits under the Weyl–Heisenberg group, a discrete group first brought into quantum mechanics by Weyl [13]. For \(d \le 3\) it has been proved that every SIC arises in this way [7, 8], and for all prime d that the Weyl–Heisenberg group is the only possible group [14]. (The exception is generated, when \(d = 8\), by another group. Like so many exceptional structures it is related to octonions [15], and here we will assume that it can be left aside as a curiousity.)
The Weyl–Heisenberg group, and the notation we use for it, need a few words of introduction. It is generated by two unitary operators that can be represented as
The basis vectors are labelled by integers modulo d, and the phase factor \(\omega \) is a primitive dth root of unity. It is convenient to introduce yet another phase factor \(\tau = - e^{i\pi /d}\) [16], and to define the displacement operators
An orbit under the Weyl–Heisenberg group is obtained by specifying a fiducial vector \(|\psi _0\rangle \), and by forming the \(d^2\) vectors
If we require that this orbit forms a SIC, Eq. (1) turn into a set of multivariate polynomial equations for the components of the fiducial vector and their complex conjugates. With high probability, every solution is known numerically for \(d \le 50\) [10], and every numerical solution is known exactly for \(d \le 21\) [10, 17]. In addition, some exact solutions are known in higher dimensions. Beyond three dimensions the solutions are isolated, which means that the components are given by algebraic numbers, that is by roots of polynomials with integer coefficients. It is the precise nature of these numbers that is so surprising.
To get these numbers out into the open, in a representation independent way, we proceed a little differently. A key property of the Weyl–Heisenberg group is that it forms a unitary operator basis, which means that any operator on \(\mathbf{C}^d\) can be expanded in terms of the displacement operators [18]. In particular, so can the projector \(|\psi _0\rangle \langle \psi _0|\). Thus
It follows that the SIC fiducial can be reconstructed, uniquely up to an irrelevant phase, from the \(d^2-1\) phase factors
The number of independent phase factors is diminished by the symmetries possessed by the SIC, and these can be gleaned from the numerical solutions.
In the simplest non–trivial example, \(d = 4\), the symmetries of the SIC restrict the overlap phases to be
Thus there is only one independent number u. Once this number is known, the entire SIC can be reconstructed from Eq. (5). For all \(d > 4\) there are several independent numbers.
When \(d = 4\) the calculations needed to compute the phase factors \(e^{i\theta _{i,j}}\), starting from scratch by solving Eq. (1) for a fiducial vector \(|\psi _0\rangle \), can be done by hand. Quite easily in fact; this was described in a previous Växjö talk [19]. Here we simply quote the result, which is that one verifies the claims made so far, and moreover one finds that
Now the claim is that there is the beginning of a pattern here, and a connection to a major unsolved problem in mathematics, that of finding numbers generating certain interesting number fields. This beginning, and this connection, are revealed once we understand the nature of the number u.
3 The Number Field of the Example
Our first concern is to determine the smallest number field to which the number u belongs. Call it \(\mathbf{Q}(u)\), since it is an extension of the rational numbers. We will freely use the fact that the number field we are looking for is a subfield of the complex numbers. This gives the enterprise a concrete flavour, and simplifies some statements compared to those found in textbooks.
Starting from u, we immediately conclude that \(-u\), 1 / u, and \(-1/u\) also belong to the field. So does the number
In some ways x is more manageable than u itself, which is related to the fact that it is symmetric under exchanges \(u \leftrightarrow 1/u\). Going on in this way, we notice that
So these three numbers are in the field \(\mathbf{Q}(u)\). Clearly u can be obtained from them, which means that the field can be equivalently written as \(\mathbf{Q}(u) = \mathbf{Q}(\sqrt{5}, \sqrt{2}, i\sqrt{\sqrt{5}+1})\). Indeed the latter three generators of the field were used in the early references [10, 12]. However, the field is not yet large enough to contain the number i, or the number \(\tau = - (1+i)/\sqrt{2}\) that appears in the reconstruction formula (5). We definitely want to extend our number field so that the number \(\tau \) is included. And we want to do so in a principled way. This means that Galois theory must come into play.
Introductions to Galois theory, of book length [20] or less than that [21], are readily available, but to really appreciate them one should look at a non-trivial example first—such as the one we are concerned with here. First we ask Mathematica for the minimal polynomial, with coefficients among the integers, of the algebraic number u. Minimal polynomials of degree n always have n distinct roots, otherwise they would not be minimal (that is, have the lowest possible degree). Mathematica gives the minimal polynomial for u after only a moment’s hesitation. It is of degree 8:
This means that our field \(\mathbf{Q}(u)\) can be regarded as a vector space over the rationals, of dimension 8, since we will perform our calculations modulo the equation \(p_1(u) = 0\). For instance
Every element in the field can be expressed as a polynomial in u of a degree not exceeding seven. In general the dimension of a field, such as \(\mathbf{Q}(u)\), considered as a vector space over its ground field, in this case \(\mathbf{Q}\), is called its degree. So the conclusion so far is that
where we used standard notation for the degree of an extension field relative to its ground field. More information about the field can be obtained by studying its automorphisms, that is to say mappings of the field onto itself which respect the field operations, and which leave the ground field (in this case the rationals) invariant. This group is known as the Galois group of the field; when Galois first studied it he regarded it as the group that permutes the roots of the minimal polynomial. The order of the Galois group equals the degree of the extension.
The leading coefficient of our minimal polynomial equals 1, and it is a palindromic polynomial, in an obvious sense. The first property implies that u is an algebraic integer (by definition), and the second property implies that 1 / u is another root of same polynomial. It follows that both u and 1 / u are algebraic integers. Therefore (again by definition) u is an algebraic unit. Another peculiarity of our polynomial is that only even powers appear in it, meaning that the phase factors \(-u\) and \(-1/u\) are roots of the polynomial too.
To complete the list of phase factors appearing in Eq. (7) we also need the number \(-1\). It is a root of the polynomial \(p_0(t) = t+1\), whose leading coefficient is again 1. Therefore \(-1\) is an algebraic integer too, and because \(p_0(t)\) is palindromic it is an algebraic unit as well. In this context we call it a ‘baby unit’. Every phase factor in Eq. (7) is an algebraic unit.
Actually, the observational evidence is that the minimal polynomials of the SIC phases are always palindromic, for all d [5]. This granted, it is easy to work out the minimal polynomial \(p_1(t)\) by hand. First we find the minimal polynomial for the number \(x = u + 1/u\), namely
Thus x is an algebraic integer, but it is not a unit. Now we use the fact that whenever the minimal polynomial \(p_{2n}\) of an algebraic number z is a palindromic polynomial of degree 2n, it can be obtained as
where \(p_n(t)\) is the minimal polynomial of the number \(z + 1/z\).
But in defining the field \(\mathbf{Q}(u)\) we seem to have stopped half-way: we are not able to express all the roots of the minimal polynomial. We have to resolve this in order to bring the full power of Galois theory into the play. Thus we are looking for a normal extension of \(\mathbf{Q}\) allowing us to split the polynomial, that is to say we need to include all its roots in a field which will be larger than just \(\mathbf{Q}(u)\). Because the polynomial is palindromic and depends only on even powers we know that a full factorization must take the form
for some algebraic unit r. (It is a unit by construction.) Writing this out leads to a second degree polynomial equation for \(r^2\) with coefficients in the field \(\mathbf{Q}(u)\), which we can solve. But we can also simply guess the solution. From Eq. (10) it is evident that \(\sqrt{5}\) will be left invariant when we permute the roots that we have so far. This suggests that it should go to \(-\sqrt{5}\) under the exchange \(u \leftrightarrow r\). If so, r can be obtained by changing the sign in front of \(\sqrt{5}\) in the expression for u. If we perform the replacements
we find that
We obtain 1 / r by changing the sign in front of the second term. A direct calculation confirms that r is a root of \(p_1\).
It is even easier to show that
In particular this gives the desired expression for \(i = i(u,r)\).
Now r is obviously a root of
Hence the minimal polynomial for r, with coefficients in \(\mathbf{Q}(u)\), is
This is a second order polynomial, which means that the degree of the extension from \(\mathbf{Q}(u)\) to \(\mathbf{Q}(u,r)\) is 2.
The situation so far is that we have the number fields \(\mathbf{F}_1 = \mathbf{Q}(u)\) and \(\mathbf{F}_2 = \mathbf{F}_1(r) = \mathbf{Q}(u,r)\). The latter field is a splitting field of the minimal polynomial of u, since the polynomial admits eight roots over \(\mathbf{F}_2\). The degrees of these extensions are
The degree is always multiplicative. As a vector space over \(\mathbf{Q}\) the field \(\mathbf{F}_2\) appears as a tensor product, with a basis consisting of the sixteen monomials \(1, u, \dots , u^7, r, ru, \dots , ru^7\).
The order of the Galois group equals the degree of the extension, and this group permutes the roots of the polynomials that were used to define the field. The story becomes particularly simple when the extension is normal. If all the roots of the degree 8 polynomial had been in the field obtained by adjoining one of its roots, the extension would have been already normal, and the Galois group would have had order 8. On the other hand we might have found only one root in the first step, and would then have been left with an irreducible polynomial of order 7. The second extension would then have had degree \(8\cdot 7\) over the field of rationals. In the worst case scenario an extension of degree 8! would be needed to split the polynomial, and the Galois group would then be the symmetric group \(S_8\). Our Galois group must have the comparatively modest order 16.
Three generators of our Galois group G can be written down immediately. With an eye on the polynomial \(p_2(t)\), we find them to be
All three generators have order 2, and together they form an abelian group of order 8. Let us call it H. We need an additional element with the property that \(g_4(u) = r\). To see what it does to r we note that
where Eq. (21) was used. One solution is \(g_4(r) = u\), so we choose the fourth generator as
It is easily seen that \(g_2g_4 = g_4g_2\), which means that \(g_2\) belongs to the centre of the group. In fact \(G = Z_2\times D_8\), where \(D_8\) is a non-abelian group of order 8, easily identified with the dihedral group if we observe that \(g_1g_4\) and \(g_3g_4\) are of order 4.
Recall that \(D_8\) is the symmetry group of the square. However, we do not need to know this. The useful way to look at the structure of the group G is to observe that the abelian group H is a normal subgroup since
Hence \(G/H = Z_2\), which is abelian. Thus the Galois group is soluble. A group G is called soluble if it admits a sequence of normal subgroups \(H_k\) so that
where the notation is meant to imply that all the quotient groups \(H_k/H_{k-1}\) are abelian. The name “soluble” is chosen because Galois realized that a polynomial equation can be solved in terms of radicals if and only if its Galois group is soluble. And indeed all the known SIC fiducials, although they have a complicated appearance, do share this remarkable feature [10].
The Galois group we have arrived at admits the very short sequence
A soluble group cannot have a shorter sequence of normal subgroups without actually being abelian. Similarly short sequences appear also for SICs beyond \(d = 4\) [10, 12].
But we return to our example. The action of the generators of the group, on the numbers we have discussed, is worked out using Eqs. (10), (11), and (22). A modest amount of extra work is needed for the action of \(g_4\). The result is given in Table 1. It is interesting to observe that the generator \(g_1\) effects complex conjugation.
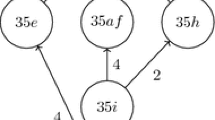
It is very interesting to observe that the subfield \(\mathbf{Q}(\sqrt{5})\) is left invariant by all transformations belonging to the subgroup H. Hence the abelian group H is the Galois group of the field considered as an extension of \(\mathbf{Q}(\sqrt{5})\). This makes the field an abelian extension of the real quadratic field \(\mathbf{Q}(\sqrt{5})\). The field \(\mathbf{E}_\mathbf{R} = \mathbf{Q}(\sqrt{5}, \sqrt{2})\) is totally real, in the sense that every embedding of this field into \(\mathbf{C}\) is real. This field can be extended to either \(\mathbf{Q}(u)\), which contains the overlap phases, or to \(\mathbf{Q}(r)\), and the two of them are related by the automorphism \(g_4\) when regarded as subfields of \(\mathbf{Q}( u,r)\), which is the field needed to construct the SIC projectors. Judging from the way the various patterns recur in higher dimensions [5, 12], the correct way of looking at the fields we have encountered is as given in Fig. 1.
4 Some Further Results I was Told About
We have reached the conclusion that the SIC phases are units in an interesting field. Now the set of units in a given field form a multiplicative unit group, and it is natural to ask how the SIC phases are positioned within that group.
There are algorithms for computing generators of unit groups, but we have to take leave of pencil and paper methods at this point. A computer algebra package such as Magma or Sage is needed for the calculation. For the field \(\mathbf{F}_1 = \mathbf{Q}(u)\) the unit group is \(Z_2\times Z\times Z \times Z \times Z \times Z\). The finite subgroup \(Z_2\) is known as the torsion subgroup, and evidently consists of the units \(\pm 1\). A possible set of generators of the infinite factors is [22]
Their minimal polynomials are of degree 2, 4, 8, 8, and 8. The generator \(u_{(1)}\) is the fundamental unit in the quadratic field \(\mathbf{Q}(\sqrt{2})\), while \(-u_{(2)}^2\) is the fundamental unit in \(\mathbf{Q}(\sqrt{5})\). The generators \(u_{(3)}\) and \(u_{(4)}\) are complex phase factors.
Remarkably, \(u_{(3)}\) is equal to the SIC phase u. Hence the SIC phase has a very special position inside the unit group. Unfortunately, for the fields arising from SICs, the unit group is known only in a handful of cases [5]. The size of the calculation grows quickly with the field—in fact calculating unit groups is one of those problems for which the best known algorithm demands a quantum computer [23].
5 How the Example Generalizes
In one sense, our example does not generalize at all: in no other case, except possibly for one of the two SIC fiducials in dimension 8, can the analogous calculations be done by hand. However, this is a practical difficulty, not a conceptual one, and, using computer algebra packages, quite a bit of progress has been made. It is found [12], quite generally, that SICs give rise to fields that are abelian extensions of the real quadratic fields \(\mathbf{Q}(\sqrt{D})\), where
(Any square factor is irrelevant, and can be divided out). Choosing \(d > 3\) appropriately, abelian extensions of every real quadratic field occur in the SIC problem, and the SIC phases provide generators for their unit groups. A main point, emerging from recent work [5], is that we now have a precise description of the relevant extensions. In all known examples they are ray class fields with conductor d (or 2d if d is even), or extensions thereof. These words carry deep meaning for algebraic number theorists. The most familiar example of a conductor is the integer n in the phase factor \(e^{2\pi i/n}\), when the rational field is extended to the cyclotomic field \(\mathbf{Q}(e^{2\pi i/n})\). Cyclotomic fields house the most general abelian extensions of \(\mathbf{Q}\), and their conductors tell us how they fit together. Considering abelian extensions of the imaginary quadratic fields \(\mathbf{Q}(\sqrt{-D})\) one is led to replace the exponential function with special functions defined on suitable elliptic curves. It seems that, if we want to deal with abelian extensions of the real quadratic field \(\mathbf{Q}(\sqrt{D})\), SICs provide very valuable insights. Some of the details, and how they relate to Kronecker’s Jugendtraum and to Hilbert’s unsolved 12th problem [24], are described in a contribution to this issue by Appleby et al. [25].
Coming back to the question whether SICs exist in all dimensions, if we knew the field and its unit group, and if we had enough information about the position of the SIC phases within the unit group, the question might not look so formidable anymore.
Finally, the reader may well ask for the physical significance of all this. The answer is not known. But the idea that quantum theory unquestioningly accepts the continuum has been effectively contradicted: on the contrary, elementary quantum theory seems to know about some of the deepest discrete structures hidden inside the continuum. This suggests that any challenge to the continuum has to go through quantum mechanics, not around it.
References
Schrödinger, E.: Science and Humanism. Cambridge University Press, Cambridge (1951)
Renes, J.M., Blume-Kohout, R., Scott, A.J., Caves, C.M.: Symmetric informationally complete quantum measurements. J. Math. Phys. 45, 2171 (2004)
Zauner, G.: Quantendesigns. Grundzüge einer nichtkommutativen Designtheorie. Ph.D. thesis, Univ. Wien (1999). Available in English translation in Int. J. Quantum Inf. 9, 445 (2011)
Fuchs, C.A., Schack, R.: Quantum-Bayesian coherence: the no-nonsense version. Rev. Mod. Phys. 85, 1693 (2013)
Appleby, M., Flammia, S., McConnell, G., Yard, J.: Generating ray class fields of real quadratic fields via complex equiangular lines. arXiv:1604.06098
Appleby, D.M.: SIC-POVMs and MUBs: Geometrical relationships in prime dimensions. In: Accardi, L. et al. (eds.) Proceedings of the Växjö Conference on Foundations of Probability and Physics - 5, AIP Conf. Proc. 1101, New York (2009)
Szöllősi, F.: All complex equiangular tight frames in dimension 3. arXiv:1402.6429
Hughston, L.P., Salamon, S.M.: Surveying points in the complex projective plane. Adv. Math. 286, 1017 (2016)
Andersson, D., Bengtsson, I., Blanchfield, K., Dang, H.B.: States that are far from being stabilizer states. J. Phys. A 48, 345301 (2015)
Scott, A.J., Grassl, M.: SIC-POVMs: A new computer study. J. Math. Phys. 51, 042203 (2010)
Private communication from Andrew Scott
Appleby, D.M., Yadsan-Appleby, H., Zauner, G.: Galois automorphisms of symmetric measurements. Quant. Inf. Comp. 13, 672 (2013)
Weyl, H.: Theory of Groups and Quantum Mechanics. Dutton, New York (1932)
Zhu, H.: SIC-POVMs and Clifford groups in prime dimensions. J. Phys. A 43, 305305 (2010)
Stacey, B.C.: Sporadic SICs and the normed division algebras. arXiv:1605.01426
Appleby, D.M.: SIC-POVMs and the extended Clifford group. J. Math. Phys. 46, 052107 (2005)
Appleby, M., Chien, T.-Y., Flammia, S., Waldron, S. to appear. See also T.-Y. Chien: Equiangular lines, projective symmetries and nice error frames, PhD thesis, Univ. of Auckland (2015)
Schwinger, J.: Unitary operator bases. Proc. Natl. Acad. Sci. 46, 570 (1960)
Bengtsson, I.: A remarkable representation of the Clifford group. In: Jaeger, G. et al. (eds.), Proceedings of the Växjö Conference on Advances in Quantum Theory. AIP Conf. Proc. 1327, New York (2011)
Stewart, I.: Galois Theory. Chapman and Hall, London (1973)
Yadsan-Appleby, H.: Gaussian and covariant processes in discrete and continuous variable quantum information. Ph.D. Thesis, Univ. College London (2012)
Private communication from Marcus Appleby and Gary McConnell
Schmidt, A., Vollmer, U.: Polynomial time quantum algorithm for the computation of the unit group of a number field. In: Proceedings of the 37th Annual ACM Symposium on Theory of Computing, ACM (2005)
Manin, Y.I.: Real multiplication and noncommutative geometry (ein Alters- traum). In: Laudal, O.A., Piene, R. (eds.) The Legacy of Niels Henrik Abel. Springer, Berlin (2004)
Appleby, M., Flammia, S., McConnell, G., Yard, J.: SICs and algebraic number theory (in this issue)
Author information
Authors and Affiliations
Corresponding author
Additional information
Talk at the Växjö conference ‘Quantum and Beyond’, June 2016.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bengtsson, I. The Number Behind the Simplest SIC–POVM. Found Phys 47, 1031–1041 (2017). https://doi.org/10.1007/s10701-017-0078-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-017-0078-3