About Possible Extensions of Quantum Theory

Abstract

Recently it has been claimed that no extension of quantum theory can have improved predictive power, the statement following, according to the authors, from the assumptions of free will and of the correctness of quantum predictions concerning the correlations of measurement outcomes. Here we prove that the argument is basically flawed by an inappropriate use of the assumption of free will. In particular, among other implications, the claim, if correct, would imply that Bohmian Mechanics is incompatible with free will. This statement, appearing in the paper, derives from the unjustified identification of free will with the no-signaling constraint and of a purely formal and not physical use of such a constraint.

Appendix: An Oversimplified Completion of Quantum Mechanics

We present here an extremely simplified model of a deterministic hidden variable theory, which is a more elegant and symmetric (from the point of view of its nonlocal features) reformulation of Bell’s famous example [4] of a nonlocal deterministic hidden variable theory for the correlations of the singlet state. Such a model has been recently discussed [2] by the two of us, with reference to a proposal put forward by Leggett [3]. Exactly as Bohmian mechanics, this model satisfies the aforementioned assumption QM, but it fails to fulfill FR, as we shortly prove.

The model goes as follows. One considers the system of two identical spin 1/2 particles in the singlet state, which at a given time t (in a given reference frame) are confined to two far away space regions and can be subjected to experiments aimed to ascertain the value of their spin components along two freely chosen space directions a and b. The system is characterized by the assignement of the state vector ψ (which in our case is the singlet) and by a hidden variable λ, which is a unit vector in the three dimensional real space and is assumed to be uniformly distributed on the surface of the unit sphere. One then assumes:

• In the case in which only one of the subsystems is subjected to a measurement the value taken by σ ⁽¹⁾⋅a is given by $A_{\psi}(\mathbf{a},\mathbf{b},\lambda) = {\rm sgn}(\mathbf{a}\cdot\lambda)$, and similarly for σ ⁽²⁾⋅b, with outcome $B_{\psi }(\mathbf{a},\mathbf{b},\lambda) = - {\rm sgn}(\mathbf{b}\cdot\lambda)$.

• On the contrary, if two measurements are performed, the assignment of λ uniquely and nonlocally determines the outcomes as follows: $A_{\psi}(\mathbf{a},\mathbf{b},\lambda) = {\rm sgn}({\hat{\mathbf{a}}}\cdot\lambda)$ and $B_{\psi}(\mathbf{a},\mathbf{b},\lambda) = - {\rm sgn}({\hat{\mathbf{b}}}\cdot\lambda)$, where the vectors $\hat{\mathbf{a}}$ and $\hat{\mathbf{b}}$ lie in the plane identified by a and b, and are obtained by these vectors by rotating them in such a way that they are still symmetrically disposed with respect to the bisector of the angle ω (with 0≤ω≤π) between a and b, and form an angle $\hat{\omega}$ satisfying, as in the case of Bell’s model, $\hat{\omega} = \pi\sin^{2}\frac{\omega}{2}$. Notice that $\hat{\omega}\leq\omega$ when ω≤π/2, and $\hat{\omega } \geq\omega$ when ω>π/2.

By using the above relations one can easily prove that the model, when the appropriate average over λ is performed, is predictively equivalent to quantum mechanics. Stated differently, it represents, just as Bohmian mechanics, a precise extension (even though limited to the singlet state) of quantum mechanics.

In what follows, we will consider the case in which X is the value of the observable σ ⁽¹⁾⋅a, A is the space of the settings a, B is the space of the settings b for the observable σ ⁽²⁾⋅b, C stays for the space of the hidden variable and Z=λ for a precise value of the hidden variable itself. However, the reader will not encounter any difficulty in understanding the argument keeping in mind these specifications, even though, for simplicity, we will continue to use the generic expressions for the conditional probabilities.

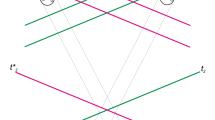
We consider P _XZ|AC , and we take into account that this probability is different from zero only for X=±1 and takes the value +1 when X=+1 and a⋅λ>0 and the value 0 when X=+1 and a⋅λ<0 (the two values must be exchanged when the probabilities refer to the outcome −1). We can now evaluate P _XZ|ABC . From the prescriptions given above, for some values of a and λ, it is possible to choose the setting b in such a way to make P _XZ|ABC =0 when, for the considered λ, P _XZ|AC =1. Actually, for simplicity let us align λ with the z-direction and suppose that the angle between a and λ is θ≤π/2, as shown in Fig. 1. Let us now consider the direction $\mathbf{a_{\perp}}$ and let us choose b lying between $\mathbf{a_{\perp}}$ and ${\bf-a}$. Since the angle ω between a and b is greater than π/2, according to the rules governing our model, ${\hat{\mathbf{a}}}$ is rotated, in the clockwise direction, of an amount

$$ \frac{\hat{\omega} - \omega}{2} = \frac{\pi}{2} \sin^{2}\frac{\omega }{2} - \frac{\omega}{2} $$

(10)

with respect to a. If this amount is greater than $\frac{\pi }{2} - \theta$, i.e., if θ satisfies the relation

$$ \theta> \frac{\pi}{2}\cos^{2}\frac{\omega}{2} + \frac{\omega}{2}, $$

(11)

the quantity $\hat{\mathbf{a}} \cdot\lambda$ has opposite sign with respect to a⋅λ and, correspondingly, P _XZ|ABC =0. It turns out that, when π/2<ω<π, condition (11) is always compatible with θ≤π/2, and then the model does not respect the non-signaling constraint imposed to any extension of quantum mechanics in Ref. [1]. Therefore, it does not satisfy Eqs. (1).

Fig. 1

Values of a,b and λ for which the non-signaling constraints are violated

One might object that our example (which holds only for a specific state ψ) is too simplified to allow general conclusions of the sort we have drawn. However, such an objection would be totally out of the target. In fact, anybody familiar with Bohmian mechanics (the paradigmatic example of a hidden variable extension of quantum mechanics) knows very well that, in the case of two far away spin 1/2 particles in an entangled state, a situation which mirrors perfectly the one we have presented, occurs quite naturally. Typically, for a given state vector ψ, for given values of the positions of the particles (the hidden variables) and for some fixed choice of the setting of the apparatus in A, an observer in B can perform an appropriate choice for the setting of his apparatus in such a way that P _XZ|ABC differs from P _XZ|AC (obviously here C stays for the positions of the particles and Z for their precise values). So, also in this case, Eqs. (1) are violated.