Abstract
Some problems in finding a complete quantum theory incorporating gravity are discussed. One is that of giving a consistent unitary description of high-energy scattering. Another is that of giving a consistent quantum description of cosmology, with appropriate observables. While string theory addresses some problems of quantum gravity, its ability to resolve these remains unclear. Answers may require new mechanisms and constructs, whether within string theory, or in another framework.





Similar content being viewed by others
Notes
For further discussion, see [5].
We adopt the convention \(M_{D}^{D-2} = (2\pi)^{D-4}/(8\pi G_{D})\).
Even theories without Lorentz invariance, e.g. with modified dispersion relations, appear to need to address such a regime, or confront even greater complications. One example would be in black hole formation from non-relativistic particles.
More precisely, we might think about the perturbative expansion around the classical geometry corresponding to the saddlepoint in the eikonal amplitude. This will be described below.
Note that one can consider either tree diagrams with all but one free “field-point” leg connected to the high-energy sources, which gives an analog to the calculation of the classical metric of [24, 25], or with all legs connected to the external sources, corresponding to contributions to the two-two amplitude like in Fig. 2. These are clearly related, and argued to have corresponding divergences at (2.11).
One also might try semicompact sources like those described in [54]. The expression (3.11) would not give compact F, but needs to be modified to take into account the extent of the source. This remains an open question, though one also expects to encounter difficulties either like those outlined in the previous or next subsections.
I thank T. Okuda and J. Polchinski for discussions on this point.
For a gaussian wavepacket, the longitudinal width of the packet must satisfy
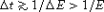 , which places a bound on the amplitude for tails of wavepackets colliding at zero impact parameter to be “outside” the horizon:
, which places a bound on the amplitude for tails of wavepackets colliding at zero impact parameter to be “outside” the horizon:  . Similar arguments can be given for transverse widths.
. Similar arguments can be given for transverse widths.I thank J. Polchinski and M. Gary for discussions on this point.
References
Hawking, S.W.: Particle creation by black holes. Commun. Math. Phys. 43, 199 (1975) [Erratum-ibid. 46, 206 (1976)]
Hawking, S.W.: Breakdown of predictability in gravitational collapse. Phys. Rev. D 14, 2460 (1976)
Bousso, R., Freivogel, B., Leichenauer, S., Rosenhaus, V.: Eternal inflation predicts that time will end. arXiv:1009.4698 [hep-th]
Horowitz, G.T.: Surprising connections between general relativity and condensed matter. arXiv:1010.2784 [gr-qc]
Giddings, S.B.: The gravitational S-matrix: Erice lectures. arXiv:1105.2036 [hep-th]
Weinberg, S.: Infrared photons and gravitons. Phys. Rev. B 140, 516 (1965)
Donoghue, J.F., Torma, T.: Infrared behavior of graviton-graviton scattering. Phys. Rev. D 60, 024003 (1999). hep-th/9901156
’t Hooft, G.: Graviton Dominance in Ultrahigh-Energy Scattering. Phys. Lett. B 198, 61–63 (1987)
Amati, D., Ciafaloni, M., Veneziano, G.: Classical and quantum gravity effects from Planckian energy superstring collisions. Int. J. Mod. Phys. A 3, 1615–1661 (1988)
Amati, D., Ciafaloni, M., Veneziano, G.: Can space-time be probed below the string size? Phys. Lett. B 216, 41 (1989)
Amati, D., Ciafaloni, M., Veneziano, G.: Higher order gravitational deflection and soft Bremsstrahlung in planckian energy superstring collisions. Nucl. Phys. B 347, 550 (1990)
Amati, D., Ciafaloni, M., Veneziano, G.: Effective action and all order gravitational eikonal at Planckian energies. Nucl. Phys. B 403, 707 (1993)
Banks, T., Fischler, W.: A Model for high-energy scattering in quantum gravity. hep-th/9906038
Muzinich, I.J., Soldate, M.: High-energy unitarity of gravitation and strings. Phys. Rev. D 37, 359 (1988)
Verlinde, H.L., Verlinde, E.P.: Scattering at Planckian energies. Nucl. Phys. B 371, 246 (1992). arXiv:hep-th/9110017
Kabat, D., Ortiz, M.: Eikonal quantum gravity and Planckian scattering. Nucl. Phys. B 388, 570 (1992). arXiv:hep-th/9203082
Giddings, S.B.: Locality in quantum gravity and string theory. Phys. Rev. D 74, 106006 (2006). arXiv:hep-th/0604072
Giddings, S.B., Gross, D.J., Maharana, A.: Gravitational effects in ultrahigh-energy string scattering. Phys. Rev. D 77, 046001 (2008). arXiv:0705.1816 [hep-th]
Giddings, S.B., Srednicki, M.: High-energy gravitational scattering and black hole resonances. Phys. Rev. D 77, 085025 (2008). arXiv:0711.5012 [hep-th]
Giddings, S.B., Schmidt-Sommerfeld, M., Andersen, J.R.: High energy scattering in gravity and supergravity. Phys. Rev. D 82, 104022 (2010). arXiv:1005.5408 [hep-th]
Bern, Z., Dixon, L.J., Roiban, R.: Is N = 8 supergravity ultraviolet finite? Phys. Lett. B 644, 265 (2007). arXiv:hep-th/0611086
Eardley, D.M., Giddings, S.B.: Classical black hole production in high-energy collisions. Phys. Rev. D 66, 044011 (2002). arXiv:gr-qc/0201034
Giddings, S.B., Porto, R.A.: The gravitational S-matrix. Phys. Rev. D 81, 025002 (2010). arXiv:0908.0004 [hep-th]
Duff, M.J.: Covariant gauges and point sources in general relativity. Ann. Phys. 79, 261 (1973)
Duff, M.J.: Quantum tree graphs and the Schwarzschild solution. Phys. Rev. D 7, 2317 (1973)
Aichelburg, P.C., Sexl, R.U.: On the Gravitational field of a massless particle. Gen. Relativ. Gravit. 2, 303 (1971)
Choptuik, M.W., Pretorius, F.: Ultra relativistic particle collisions. Phys. Rev. Lett. 104, 111101 (2010). arXiv:0908.1780 [gr-qc]
Amati, D., Ciafaloni, M., Veneziano, G.: Towards an S-matrix description of gravitational collapse. J. High Energy Phys. 0802, 049 (2008). arXiv:0712.1209 [hep-th]
Callan, C.G. Jr., Giddings, S.B., Harvey, J.A., et al.: Evanescent black holes. Phys. Rev. D 45, 1005–1009 (1992) hep-th/9111056
Giddings, S.B., Nelson, W.M.: Quantum emission from two-dimensional black holes. Phys. Rev. D 46, 2486 (1992). arXiv:hep-th/9204072
Strominger, A.: Les Houches lectures on black holes. arXiv:hep-th/9501071
Giddings, S.B.: Quantum mechanics of black holes. arXiv:hep-th/9412138
Giddings, S.B.: The black hole information paradox. arXiv:hep-th/9508151
Lowe, D.A., Polchinski, J., Susskind, L., Thorlacius, L., Uglum, J.: Black hole complementarity versus locality. Phys. Rev. D 52, 6997 (1995). arXiv:hep-th/9506138
Giddings, S.B.: Nonlocality versus complementarity: A Conservative approach to the information problem. Class. Quantum Gravity 28, 025002 (2011). arXiv:0911.3395 [hep-th]
Banks, T., Susskind, L., Peskin, M.E.: Difficulties for the evolution of pure states into mixed states. Nucl. Phys. B 244, 125 (1984)
Susskind, L.: Trouble for remnants. arXiv:hep-th/9501106
Giddings, S.B.: Why aren’t black holes infinitely produced? Phys. Rev. D 51, 6860 (1995). arXiv:hep-th/9412159
Page, D.N.: Information in black hole radiation. Phys. Rev. Lett. 71, 3743 (1993). arXiv:hep-th/9306083
Veneziano, G.: String-theoretic unitary S-matrix at the threshold of black-hole production. J. High Energy Phys. 0411, 001 (2004). hep-th/0410166
’t Hooft, G.: Dimensional reduction in quantum gravity. arXiv:gr-qc/9310026
Susskind, L.: The world as a hologram. J. Math. Phys. 36, 6377 (1995). arXiv:hep-th/9409089
Giddings, S.B.: Flat-space scattering and bulk locality in the AdS/CFT correspondence. Phys. Rev. D 61, 106008 (2000). arXiv:hep-th/9907129
Giddings, S.B.: The boundary S-matrix and the AdS to CFT dictionary. Phys. Rev. Lett. 83, 2707 (1999). arXiv:hep-th/9903048
Aharony, O., Gubser, S.S., Maldacena, J.M., Ooguri, H., Oz, Y.: Large N field theories, string theory and gravity. Phys. Rep. 323, 183 (2000). arXiv:hep-th/9905111
Fitzpatrick, A.L., Katz, E., Poland, D., Simmons-Duffin, D.: Effective conformal theory and the flat-space limit of AdS. arXiv:1007.2412 [hep-th]
Polchinski, J.: S-matrices from AdS spacetime. arXiv:hep-th/9901076
Susskind, L.: Holography in the flat space limit. arXiv:hep-th/9901079
Gubser, S.S., Klebanov, I.R., Polyakov, A.M.: Gauge theory correlators from non-critical string theory. Phys. Lett. B 428, 105 (1998). arXiv:hep-th/9802109
Witten, E.: Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 2, 253 (1998). arXiv:hep-th/9802150
Gary, M., Giddings, S.B., Penedones, J.: Local bulk S-matrix elements and CFT singularities. Phys. Rev. D 80, 085005 (2009). arXiv:0903.4437 [hep-th]
Gary, M., Giddings, S.B.: The flat space S-matrix from the AdS/CFT correspondence? Phys. Rev. D 80, 046008 (2009). arXiv:0904.3544 [hep-th]
Reed, M., Simon, B.: Methods of Mathematical Physics. Scattering Theory, Vol. 3. Academic Press, New York (1979). 463p.
Marolf, D.: Unitarity and Holography in Gravitational Physics. Phys. Rev. D 79, 044010 (2009). arXiv:0808.2842 [gr-qc]
Heemskerk, I., Penedones, J., Polchinski, J., Sully, J.: Holography from conformal field theory. J. High Energy Phys. 0910, 079 (2009). arXiv:0907.0151 [hep-th]
Gary, M., Giddings, S.B.: to appear
Giddings, S.B., Marolf, D., Hartle, J.B.: Observables in effective gravity. Phys. Rev. D 74, 064018 (2006). arXiv:hep-th/0512200
Gary, M., Giddings, S.B.: Relational observables in 2d quantum gravity. Phys. Rev. D 75, 104007 (2007). arXiv:hep-th/0612191
Veneziano, G.: A stringy nature needs just two constants. Europhys. Lett. 2, 199 (1986)
Gross, D.J.: Superstrings and unification. PUPT-1108 Plenary Session talk given at 24th Int. Conf. on High Energy Physics, Munich, West Germany, Aug 4–10, 1988
Giddings, S.B., Lippert, M.: Precursors, black holes, and a locality bound. Phys. Rev. D 65, 024006 (2002). arXiv:hep-th/0103231
Giddings, S.B., Lippert, M.: The information paradox and the locality bound. Phys. Rev. D 69, 124019 (2004). arXiv:hep-th/0402073
Giddings, S.B.: Black hole information, unitarity, and nonlocality. Phys. Rev. D 74, 106005 (2006). arXiv:hep-th/0605196
Giddings, S.B.: (Non)perturbative gravity, nonlocality, and nice slices. Phys. Rev. D 74, 106009 (2006). arXiv:hep-th/0606146
Giddings, S.B., Marolf, D.: A Global picture of quantum de Sitter space. Phys. Rev. D 76, 064023 (2007). arXiv:0705.1178 [hep-th]
Giddings, S.B.: Quantization in black hole backgrounds. Phys. Rev. D 76, 064027 (2007). arXiv:hep-th/0703116
Giddings, S.B., Sloth, M.S.: Semiclassical relations and IR effects in de Sitter and slow-roll space-times. J. Cosmol. Astropart. Phys. 1101, 023 (2011). arXiv:1005.1056 [hep-th]
Susskind, L., Thorlacius, L., Uglum, J.: The stretched horizon and black hole complementarity. Phys. Rev. D 48, 3743 (1993). arXiv:hep-th/9306069
Sekino, Y., Susskind, L.: Fast scramblers. J. High Energy Phys. 0810, 065 (2008). arXiv:0808.2096 [hep-th]
Acknowledgements
This work was supported in part by the Department of Energy under Contract DE-FG02-91ER40618. I thank G. Horowitz and D. Marolf for comments on a draft of part of this paper, and M. Gary and J. Polchinski for useful discussions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Giddings, S.B. Is String Theory a Theory of Quantum Gravity?. Found Phys 43, 115–139 (2013). https://doi.org/10.1007/s10701-011-9612-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-011-9612-x




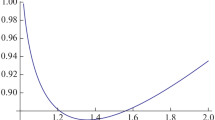
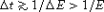 , which places a bound on the amplitude for tails of wavepackets colliding at zero impact parameter to be “outside” the horizon:
, which places a bound on the amplitude for tails of wavepackets colliding at zero impact parameter to be “outside” the horizon:  . Similar arguments can be given for transverse widths.
. Similar arguments can be given for transverse widths.