Abstract
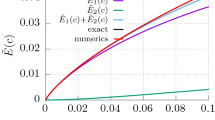
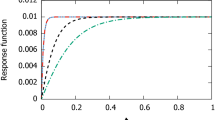
The fluctuation-dissipation theorem is a central theorem in nonequilibrium statistical mechanics by which the evolution of velocity fluctuations of the Brownian particle under a fluctuating environment is intimately related to its dissipative behavior. This can be illuminated in particular by an example of Brownian motion in an ohmic environment where the dissipative effect can be accounted for by the first-order time derivative of the position. Here we explore the dynamics of the Brownian particle coupled to a supraohmic environment by considering the motion of a charged particle interacting with the electromagnetic fluctuations at finite temperature. We also derive particle’s equation of motion, the Langevin equation, by minimizing the corresponding stochastic effective action, which is obtained with the method of Feynman-Vernon influence functional. The fluctuation-dissipation theorem is established from first principles. The backreaction on the charge is known in terms of electromagnetic self-force given by a third-order time derivative of the position, leading to the supraohmic dynamics. This self-force can be argued to be insignificant throughout the evolution when the charge barely moves. The stochastic force arising from the supraohmic environment is found to have both positive and negative correlations, and it drives the charge into a fluctuating motion. Although positive force correlations give rise to the growth of the velocity dispersion initially, its growth slows down when correlation turns negative, and finally halts, thus leading to the saturation of the velocity dispersion. The saturation mechanism in a supraohmic environment is found to be distinctly different from that in an ohmic environment. The comparison is discussed.
Similar content being viewed by others
References
Pathria, P.K.: Statistical Mechanics, 2nd edn. Butterworth-Heinemann, Oxford (1996)
Bhattacharjee, J.K.: Statistical Physics: Equilibrium and Non Equilibrium Aspects. Allied Pub., Indianapolis (2001)
Caldeira, A.O., Leggett, A.J.: Physica A 121, 587 (1983)
Caldeira, A.O., Leggett, A.J.: Ann. Phys. 149, 374 (1983)
Leggett, A.J., et al.: Rev. Mod. Phys. 59, 1 (1987)
Schwinger, J.: J. Math. Phys. 2, 407 (1961)
Keldysh, L.V.: Sov. Phys. JETP 20, 1018 (1965)
Feynman, R., Vernon, F.: Ann. Phys. 24, 118 (1963)
Grabert, H., Schramm, P., Ingold, G.L.: Phys. Rep. 168, 115 (1988)
Hu, B.L., Paz, J.P., Zhang, Y.: Phys. Rev. D 45, 2843 (1992)
Hu, B.L., Paz, J.P., Zhang, Y.: Phys. Rev. D 47, 1576 (1993)
Johnson, P.R., Hu, B.L.: Found. Phys. 35, 1117 (2005)
Oron, O., Horwitz, L.P.: Relativistic Brownian motion in 3+1 dimensions. e-Print: math-ph/0312003
Unruh, W.G., Zurek, W.H.: Phys. Rev. D 40, 1071 (1989)
Hsiang, J.-T., Lee, D.-S.: Phys. Rev. D 73, 065022 (2006)
Hsiang, J.-T., Lee, D.-S., Wu, C.-H.: J. Korean Phys. Soc. 49, 742 (2006)
Rohrlich, F.: Phys. Rev. E 77, 046609 (2008)
Rohrlich, F.: Classical Charged Particles, 3rd edn. World Scientific, Singapore (2007)
Hsiang, J.-T., Wu, T.-H., Lee, D.-S.: Phys. Rev. D 77, 105021 (2008)
Hsiang, J.-T., Wu, T.-H., Lee, D.-S.: Stochastic dynamics of a point charge under electromagnetic squeezed vacuum fluctuations. arXiv:0809.4100 [quant-ph]
Yu, H.-W., Ford, L.H.: Phys. Rev. D 70, 065009 (2004)
Ford, L.H., Roman, T.A.: Phys. Rev. D 72, 105010 (2005)
Jackson, J.D.: Classical Electrodynamics, 3rd edn. Wiley, New York (1998)
Gardiner, C.W., Zoller, P.: Quantum Noise, 2nd edn. Springer, Berlin (2000)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hsiang, JT., Wu, TH. & Lee, DS. Brownian Motion of a Charged Particle in Electromagnetic Fluctuations at Finite Temperature. Found Phys 41, 77–87 (2011). https://doi.org/10.1007/s10701-009-9333-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-009-9333-6