Abstract
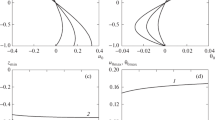
The stability of advective flow in a rotating infinite horizontal fluid layer with rigid bound-aries is investigated for a small Prandtl number Pr = 0.1 and various Taylor numbers for perturbations of the hydrodynamic type. Within the framework of the linear theory of stability, neutral curves describing the dependence of the critical Grashof number on the wave number are obtained. The behavior of finite-amplitude perturbations beyond the stability threshold is studied numerically.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
S. N. Aristov and P. G. Frik, Dynamics of large-scale flows in thin fluid layers [preprint, in Russian], Institute of Continuum Mechanics, Ural Branch of the Academy of Sciences of the USSR, Sverdlovsk (1987).
J. Pedloski, Geophysical Fluid Dynamics, Springer Verlag, Berlin, etc. (1982).
S. N. Aristov and K. G. Shvartz, “Stability of advective flow in a rotating horizontal fluid layer, ” Fluid Dynamics, 34, No.4, 457–464 (1999).
K. G. Schwarz, “Finite-amplitude spatial perturbations of advective flow in a rotating horizontal fluid layer,” Vychisl. Tekhnologii, 6, Special Issue, Pt 2 (Transactions of the International Conference RDAMM-2001, 702–707 (2001).
E. L. Tarunin and K. G. Schwarz, “Investigation of the linear stability of advective flow by the grid method,” Vychisl. Tekhnologii, 6, No.6, 108–117 (2001).
K. G. Schwarz, “Instability of advective flow in rotating horizontal layer of liquid,” Selected Papers of the International Conference ‘Fluxes and Structures in Fluids’, St. Petersburg, Russia, June 23–26, 2003, IPM RAS, Moscow, 164–171 (2004).
G. Z. Gershuni, E. M. Zhukhovitsky, and V. M. Myznikov, “Stability of plane-parallel convective flow in a horizontal layer,” Prikl. Mat. Tekhn. Fiz., No. 1, 95–100 (1974).
G. Z. Gershuni, E. M. Zhukhovitsky, and V. M. Myznikov, “Stability of plane-parallel convective fluid flow in a horizontal layer with respect to spatial perturbations,” Prikl. Mat. Tekhn. Fiz., No. 5, 145–147 (1974).
G. Z. Gershuni, P. Laure, V. M. Myznikov, B. Roux, and E. M. Zhukhovitsky, “On the stability of plane-parallel advective flows in long horizontal layers,” Microgravity Q., 2, No. 3, 141–151 (1992).
V. M. Myznikov, “Finite-amplitude convective fluid flows in a horizontal layer with a longitudinal temperature gradient,” Mathematical Models of Fluid Flows: Transactions of VI Soviet-Union Seminar on Numerical Methods in Viscous Fluid Mechanics [in Russian], Institute of Theoretical and Applied Mechanics, Siberian Branch of the Academy of Sciences of the USSR, Novosibirsk, 176–186 (1978).
G. Z. Gershuni and E. M. Zhukhovitsky, Convective Stability of an Incompressible Fluid [in Russian], Nauka, Moscow (1972).
E. L. Tarunin, Numerical Experiment in Problems of Free Convection [in Russian], Irkutsk University Press, Irkutsk (1990).
B. P. Demidovich, I. A. Maron, and E. Z. Shuvalova, Numerical Methods of Analysis: Approximation of Functions and Differential and Integral Equations [in Russian], Nauka, Moscow (1967).
Additional information
__________
Translated from Izvestiya Rossiiskoi Academii Nauk, Mekhanika Zhidkosti i Gaza, No. 2, 2005, pp. 29–38.
Original Russian Text Copyright © 2005 by Schwarz.
Rights and permissions
About this article
Cite this article
Schwarz, K.G. Effect of Rotation on the Stability of Advective Flow in a Horizontal Fluid Layer at a Small Prandtl Number. Fluid Dyn 40, 193–201 (2005). https://doi.org/10.1007/s10697-005-0059-7
Received:
Issue Date:
DOI: https://doi.org/10.1007/s10697-005-0059-7