Abstract
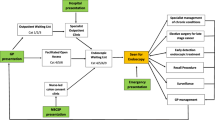
This paper is devoted to the design and analysis of the gastroenterology (GI) clinic in the Digestive Health Center (DHC) of University of Wisconsin Health. The DHC will consolidate several existing clinic and endoscopy locations into a single center. First, the work flow at a current GI clinic is studied. A Markov chain model is developed and then extended to non-Markovian case to evaluate patient average length of stay and staff utilization. The model is validated by the data observed in the clinic. It is shown that the model can provide accurate estimation of system performance. Then, using such a model, design options of the new GI clinic in the DHC are studied. To investigate the impact of different system configurations, what-if analyses are carried out and different patient check-out processes are investigated. Finally, recommendations for enhancing service at the new GI clinic are proposed to the DHC leadership.









Similar content being viewed by others
References
Bekker R, de Bruin AM (2010) Time-dependent analysis for refused admissions in clinical wards. Ann Oper Res 178:45–65
Brailsford SC (2007) Advances and challenges in healthcare simulation modeling: tutorial. In: Proceedings of the 39th winter simulation conference, pp 1436–1448
Cono M, Dawson KA (1993) Determining the size of the gastroenterology division expansion using simulation: a case study. Proc Ann HIMSS Conf 2:127–137
Fomundam S, Herrmann JW A survey of queuing theory applications in healthcare. Technical report, University of Maryland, College Park, MD
Gershwin SB (1993) Variance of output of a tandem production system. In: Onvaral RO, Akyildi IF (eds) Queuing networks with finite capacity. Elsevier, Amsterdam
Godfrey K (1983) Compartmental models and their application. Academic Press, London
Green LV, Soares J, Giglio JF, Green RA (2006) Using queueing theory to increase the effectiveness of emergency department provider staffing. Acad Emerg Med 13:61–68
Harrison GW (1994) Compartmental models of hospital patient occupancy patterns. In: McClean SI, Millard PH (eds) Modelling hospital resource use: a different apporach to the planning and control of health care systems. Royal Society of Medicine, London, pp 53–64
Irvine V, McClean SI, Millard PH (1994) Stochastic models for geriatric in-patient behaviour. IMA J Math Appl Med Biol 11:207–216
Jacobson SH, Hall SN, Swisher JR (2006) Discrete-event simulation of health care systems. In: Hall RW (eds) Patient flow: reducing delay in healthcare delivery. International series in operations research and management science, vol 91, pp 211–252
Li M, Meerkov SM (2000) Production variability in manufacturing systems: Bernoulli reliability case. Ann Oper Res 93:299–324
Marshall A, Vasilakis C, El-darzi E (2005) Length of stay-based patient flow models: recent developments and future directions. Healthcare Manag Sci 8:213–220
Marshall A, McClean SI, Shapcott CM, Millard PH (2003) Modelling patient duration of stay in hospital. Int Trans Oper Res 10:565–576
Mayhew L, Smith D (2008) Using queuing theory to analyse the governments 4-h completion time target in accident and emergency departments. Health Care Manag Sci 11:1121
Tan B (1998) Asymptotic variance rate of the output in production lines with finite buffers. Ann Oper Res 93:385–403
Taylor GJ, McClean SI, Millard PH (1998) Continuous time Markov model for geriatric patient behaviour. Appl Stoch Models Data Anal 13:315–323
Taylor GJ, McClean SI, Millard PH (2000) Stochastic models of geriatric patient bed occupancy behaviour. J R Stat Soc Series A 163:39–48
Wiler JL, Griffey RT, Olsen T (2011) Review of modeling approaches for emergency department patient flow and crowding research. Acad Emerg Med 18:1371–1379
Acknowledgments
The authors thank L. Woodhouse and other staff of University of Wisconsin Medical Foundation and G. Eaton, G. Tomas, A. Velando and S. Wirsbinski of University of Wisconsin - Madison for their help in the project. This work is supported in part by NSF Grant No. CMMI-1233807 and NSFC Grant No. 71301003
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
The transition events and corresponding rates from state \(S_k\) to state \(S_j\) are described below:
-
1.
For patient arrival, the following scenarios exist:
-
If \(s_1^k = Q\) (i.e., the waiting room is full, although unlikely), the patient is lost due to the space limit and no transition occurs.
-
If \(s_1^k < Q\) (there are available spaces in the waiting room), and \(\sum\nolimits _{i=2}^6 s_i^k= M\) (i.e., all rooms are occupied by the patients), then the patient has to wait, we have
$$\begin{aligned} s_1^j=s_1^k+1,\quad s_i^j= s_i^k, \quad i=2,\ldots ,6. \end{aligned}$$ -
If \(\sum\nolimits _{i=2}^6 s_i^k< M\) (i.e, not all rooms are occupied) and \(s_2^k+s_6^k < n_1\) (the clinical staff is available), then the patient does not need to wait and the patient will be roomed immediately,
$$\begin{aligned} s_2^j = s_2^k+1,\quad s_i^j = s_i^k, \quad i = 1,3,\ldots ,6. \end{aligned}$$ -
However, if \(\sum\nolimits _{i=2}^6 s_i^k< M\) and \(s_2^k+s_6^k = n_1\) (i.e., the clinical staff is busy), then the patient still needs to wait,
$$\begin{aligned} s_1^j=s_1^k+1,\quad s_i^j= s_i^k, \quad i=2,\ldots ,6, \end{aligned}$$In all three latter cases, the transition rate is \(\lambda\).
-
-
2.
When a patient finishes rooming, the following scenarios need to be considered:
-
If \(\sum\nolimits _{i=2}^6 s_i^k = M\) (all rooms are occupied), then
$$\begin{aligned} s_1^j=s_1^k,\quad s_2^j=s_2^k-1. \end{aligned}$$-
If \(s_4^k < n_2\) (the clinician is available),
$$\begin{aligned} s_3^j=s_3^k, \quad s_4^j=s_4^k+1. \end{aligned}$$Furthermore, since the resource (clinical staff) is released,
-
if \(s_5^k>0\) (there are patients waiting for check-out),
$$\begin{aligned} s_5^j=s_5^k-1,\quad s_6^j=s_6^k+1, \end{aligned}$$ -
otherwise,
$$\begin{aligned} s_5^j=s_5^k,\quad s_6^j=s_6^k. \end{aligned}$$ -
If \(s_4^k = n_2\) (the clinician is busy),
$$\begin{aligned} s_3^j = s_3^k+1, \quad s_4^j=s_4^k. \end{aligned}$$The changes in processes 5 and 6 are the same as in previous scenario (\(s_5^k>0\)).
-
-
If \(\sum\nolimits _{i=2}^6 s_i^k < M\) (not all rooms are occupied),
-
if \(s_4^k < n_2\) (the clinician is available),
$$\begin{aligned} s_3^j=s_3^k,\quad s_4^j=s_4^k+1. \end{aligned}$$Moreover,
-
if \(s_5^k>0\) (there are patients waiting for check-out),
$$\begin{gathered} s_{1}^{j} = s_{1}^{k} ,\quad s_{2}^{j} = s_{2}^{k} - 1, \hfill \\ s_{5}^{j} = s_{5}^{k} - 1,\quad s_{6}^{j} = s_{6}^{k} + 1, \hfill \\ \end{gathered}$$ -
if \(s_5^k = 0\) (there is no patient waiting for check-out) and \(s_1^k > 0\) (there are patients waiting for rooming),
$$\begin{aligned} s_1^j=s_1^k-1, \quad s_2^j=s_2^k,\\ s_5^j=s_5^k, \quad s_6^j=s_6^k, \end{aligned}$$ -
if no patient is waiting for rooming or discharge,
$$\begin{aligned} s_2^j=s_2^k-1,\quad s_i^j=s_i^k, \quad i=1,5,6. \end{aligned}$$ -
If \(s_4^k = n_2\) (the clinician is busy),
$$\begin{aligned} s_3^j=s_3^k+1,\quad s_4^j=s_4^k. \end{aligned}$$The changes in processes 1, 2, 5, and 6 are the same as in the previous case (\(s_4^k < n_2\)).
In all scenarios, the transition rate is \(c_1\).
-
-
-
3.
If clinician finishes examining, \(s_1^j=s_1^k\), \(s_2^j=s_2^k\), then
-
if \(s_2^k+s_6^k < n_1\) (the clinical staff is available),
$$\begin{aligned} s_5^j=s_5^k, \quad s_6^j=s_6^k+1, \end{aligned}$$In addition,
-
if there are patients waiting for clinician,
$$\begin{aligned} s_3^j=s_3^k-1,\quad s_4^j=s_4^k, \end{aligned}$$ -
if there is no patient waiting for clinician,
$$\begin{aligned} s_3^j=s_3^k,\quad s_4^j=s_4^k-1. \end{aligned}$$
-
-
If \(s_2^k+s_6^k = n_1\) (the clinical staff is busy),
$$\begin{aligned} s_5^j=s_5^k+1,\quad s_6^j=s_6^k. \end{aligned}$$The changes in processes 3 and 4 are the same as in previous case (\(s_2^k+s_6^k < n_1\)).
In all cases, the transition rate is \(c_2\).
-
-
4.
If any patient checks-out, then
$$\begin{aligned} s_3^j=s_3^k, \quad s_4^j=s_4^k. \end{aligned}$$In addition, the following scenarios exist:
-
If there are patients waiting for check-out,
$$\begin{aligned} s_1^j=s_1^k,\quad s_2^j=s_2^k, \\ s_5^j=s_5^k-1,\quad s_6^j=s_6^k. \end{aligned}$$ -
If there is no patient waiting for check-out, but
-
there are patients waiting for rooming,
$$\begin{aligned} s_1^j=s_1^k-1,\quad s_2^j=s_2^k+1, \\ s_5^j=s_5^k,\quad s_6^j=s_6^k-1, \end{aligned}$$ -
otherwise,
$$\begin{aligned} s_1^j&=s_1^k,\quad s_2^j=s_2^k, \\ s_5^j&=s_5^k,\quad s_6^j=s_6^k-1. \end{aligned}$$
-
-
Again, in all scenarios, the transition rate is \(c_3\)
Appendix 2
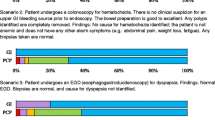
The data collected from GI clinic is summarized in Table 8. They are used in both analytical and simulation models.
Rights and permissions
About this article
Cite this article
Zhong, X., Song, J., Li, J. et al. Design and analysis of gastroenterology (GI) clinic in Digestive Health Center of University of Wisconsin Health. Flex Serv Manuf J 28, 90–119 (2016). https://doi.org/10.1007/s10696-015-9215-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10696-015-9215-5