Abstract
This paper describes selected observations, measurements, and analysis from a series of large-scale experiments on cross-laminated timber (CLT) slabs that were exposed to fire from below, using four different heating scenarios, with a sustained mechanical loading of 6.3 kN m per metre width of slab. The deflection response and in-depth timber temperatures are used to compare the experimental response against a relatively simple structural fire model to assess the load bearing capacity of CLT elements in fire, including during the decay phase of natural fires. It is demonstrated that the ventilation conditions in experiments with a fixed fuel load are important in achieving burnout of the contents before structural collapse occurs. A mechanics-based structural fire model is shown to provide reasonably accurate predictions of structural failure (or lack thereof) for the experiments presented herein. The results confirm the importance of the ventilation conditions on the fire dynamics, burning duration, and the achievement of functional fire safety objectives (i.e. maintaining stability and compartmentation), in compartments with exposed CLT.
Similar content being viewed by others
1 Background
Engineered timber products are increasingly being considered as the main structural material for progressively taller buildings. The widespread introduction of cross-laminated timber (CLT) is one of the main drivers in this development; CLT consists of timber boards that are arranged in layers with alternating directions and bonded with adhesives.
A critical consideration for the uptake of mass timber in tall buildings is structural fire safety [1], owing to the fact that timber burns and is (in at least this respect) distinct from concrete and steel, both of which are non-combustible.
Upon exposure to fire, timber will pyrolyse, producing flammable gases and an outer carbonaceous char layer. The char layer itself has negligible strength and stiffness; however, it acts as an effective insulator, reducing—but not preventing—further heat transfer into the interior of the timber member and maintaining a comparatively cooler inner core. Under standardized time temperature exposures during furnace testing, approximately 25–40 mm [2] of timber beneath the char is heated above ambient temperatures—this is sometimes referred to as the thermal penetration depth.
As timber is heated, it gradually loses strength and stiffness as a function of both temperature and moisture content [3]. Thus, the remaining structural capacity in a fire-exposed timber element depends critically on the in-depth thermal penetration and the resulting loss of mechanical properties of the heated but uncharred timber. Various approximate structural fire design methods are available which attempt to account for these effects under standard furnace testing conditions [4]—these are not of primary interest here as their scope is limited to normative (i.e. standard) fire exposures in furnaces, and they are not strictly applicable to non-standard (i.e. natural) heating conditions.
Fire safety in most buildings relies on compartmentation as part of the fire strategy to ensure life safety of building occupants and fire service personnel. To achieve this, building elements must maintain one or all of insulation, integrity, and load bearing capacity for an adequate period. In a typical ventilation-controlled compartment fire, a growth phase is followed by a period of ventilation controlled burning; this will continue at a quasi-steady rate until the fuel in the compartment is consumed and the fire enters a decay phase which is marked by reducing gas phase temperatures. Once the continuing fuel supply is insufficient to maintain burning, the gas phase temperatures in a compartment will eventually return to ambient temperatures, and heat transfer within the compartment will be dominated by the compartment boundaries. To successfully maintain compartmentation, the three above criteria for building elements must typically be maintained until the fire has burned out and the compartment boundaries have cooled down. Otherwise fire and heat may have a route to spread into adjacent compartments containing unburnt fuel, and thus compromising the safety of building occupants, emergency services, and possibly resulting in significant property or other social, cultural, and/or economic losses.
Given its combustible nature, the use of structural timber presents unique fire hazards which must be considered by designers, particularly in complex or high consequence buildings which cannot be rapidly evacuated during fire. When the original moveable fuel load (e.g. furniture) has burned out, any exposed timber may, under the right conditions, continue burning [5,6,7,8], resulting in continued charring, in-depth heating, and consequential reductions in load-bearing capacity. In the absence of active fire suppression this could result in structural collapse. Furthermore, even in cases where auto-extinction does occur (i.e. the exposed timber does not continue to burn after burnout of the moveable fuel load), in-depth heating of the timber structural elements will continue as heat continues to dissipate into the cooler parts of the timber, thereby further reducing the overall capacity well into the decay phase of the fire. This phenomenon of in-depth heating beyond burnout also occurs in reinforced concrete [9] and protected steel [10] elements; however, the hazard from this effect is considered to be comparatively greater for timber, since irreversible reductions in mechanical properties of timber can occur at temperatures as low as 60–100°C [11] (as opposed to 250°C or higher for concrete or steel). The likely continued loss of load-bearing capacity after burnout of the moveable fuel load should therefore be considered when evaluating the structural fire performance of timber elements [12,13,14]; even if auto-extinction occurs.
2 Experimental Programme
The data presented and analysed herein is taken from the test reports of the “The Epernon Fire Tests Programme” [15]. This project seeks to understand the links between normative fire resistance ratings and real fire performance in buildings. The project has several objectives, such as quantification of the energy participation of combustible materials in standard furnace tests, the influence of combustible surfaces and ventilation factors on the dynamics of compartment fires (including external flaming), and the thermomechanical behaviour of structures under standard and natural fires. Full test reports for all of the experiments are available from a project-specific website [15]. This paper presents analysis relevant to the five tests undertaken on loaded, unprotected CLT slabs exposed to fire from below.
2.1 Standard Furnace Tests on CLT Slabs
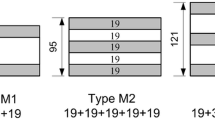
Two essentially identical standard furnace tests were performed on CLT slabs according to EN 1365-2 [16]. The slabs were 5900 mm in length and 3900 mm in width. Each specimen was comprised of two CLT panels, each with plan dimensions of 5900 mm × 1950 mm and joined together by a 150 mm wide wooden assembly strip which was laid over a sheet of ceramic paper and screwed into rabbets with a width of 76 mm and a depth of 33 that were cut into the final lamella of each panel to be joined. The 2 mm wide gap underneath this assembly was sealed by an intumescent strip with a depth of 20 mm on the exposed side (Fig. 1). The strength of the joint was not critical in terms of the load-bearing capacity as it was oriented in the spanning direction during testing. The slabs had a total thickness of 165 mm, comprising of five timber lamellae of 33 mm thickness each. All plies were orientated crosswise to each adjacent ply (as is typical for CLT) with the wood grains in the outer plies oriented in the spanning direction. The plies were face bonded together using a one-component polyurethane adhesive (PURBOND HB S709). The mean moisture content for all CLT slabs in this study was 11%, with a standard deviation of 0.1%.
The furnace temperature during the tests was controlled using 15 plate thermometers to follow the standard temperature–time curve prescribed by EN 1363-1 [17]. Temperatures measured with plate thermometers are a type of effective temperature influenced by both the gas phase temperature and the radiation exchange within the enclosure. Natural gas pre-mixed with air was injected into the furnace as fuel to promote complete combustion.
The sustained structural loading applied during fire exposure corresponded to the Eurocode [18] accidental load combination, giving a total loading density of 1.35 kN/m2 over an area of 5.6 m × 3.9 m, and thus a total imposed load of 29.5 kN. This was applied as a dead load in the form of five steel beams applying point loads over the span, as shown in Fig. 2. The midspan bending moment arising from this loading situation was 24.7 kN m, i.e. the CLT had to be able to structurally support a bending moment of 6.3 kN m per metre width of slab.
2.2 Compartment Fire Experiments on CLT Slabs
In addition to the two standardised furnace tests described above, three compartment fire experiments were carried out with an exposed CLT ceiling. The compartment walls were constructed from aerated concrete block with a thickness of 300 mm and a bulk density of 300 kg/m3. The CLT ceiling panel was manufactured, loaded, and instrumented the same way as the slabs used for the standard furnace tests, as described in Sect. 2.1.
All compartments had the same internal dimensions, these being 6 m x 4 m in plan, and 2.52 m in height. Three different opening geometries were used, as listed in Table 1. The opening factors are given using the Thomas [19] definition as \(A_{T} /A_{v} \sqrt {h_{v} }\), where \(A_{T}\) is the total internal area (excluding openings and floor), \(A_{v}\) is the opening area, and \(h_{v}\) is the opening height. All openings were on the same face of the enclosure.
In each experiment, the moveable fuel load was supplied using timber cribs. Six cribs were used in each of the natural fire tests, with each consisting of 12 rows of five sticks each measuring 90 mm × 90 mm in cross section and 1 m in length. The fire was ignited using a 3 litre heptane pool fire beneath each crib. This resulted in a total imposed fuel load, including from heptane, of approximately 891 MJ/m2 for each experiment; this is considered representative of dwellings [20] (note, however, that this does not include the contribution from the exposed CLT). The pseudo-steady burning phase of Scenario 1 is shown in Fig. 3, showing burning of the wood cribs and flames exiting the compartment, thus indicating flashover.
2.3 Instrumentation
The CLT slabs tested in the standard furnace tests and those in the compartment fire experiments were, unless stated otherwise, each instrumented identically, as described in this section.
Vertical deflections during testing were recorded using two displacement transducers at midspan, along with one at each end along the panel’s centreline.
In-depth temperatures within the timber were recorded by 1.5 mm diameter Inconel sheathed Type K thermocouples (TCs), placed in four groups each located at 1770 mm from the slab centre on a diagonal between the corners of the slab. At each location, ten in-depth TCs were installed at distances of 0, 4, 12, 23, 33, 44, 55, 66, 77, and 99 mm from the fire-exposed surface. Additionally, one thermocouple was installed projecting 10 mm beyond the exposed face of the CLT to measure the gas temperature, as shown in Fig. 4. One TC was installed on the back (i.e. upper) face of the slab. The resulting TC layout at each plan measurement location is shown in Fig. 4. Thermocouples were installed along grooves during the CLT panel manufacture so as to minimise errors in placement position. Thermocouples not located along a glue line were installed along the grooves, and then inserted into pre-drilled holes from the rear of the lamella, as illustrated in Fig. 4. For the experiment labelled Scenario 3, additional Inconel sheathed thermocouples were inserted at 33, 66, 77, 88, 99, 110, 121, 132, 143 and 154 mm from the fire exposed surface; this was because longer burning durations and deeper thermal penetration were expected. It should be noted that, since these additional thermocouples were inserted from the back, they can be influenced by conduction errors which can lead to a systematic underestimation of the true temperatures in locations without any thermocouples [21, 22].
The temperatures in the enclosure were monitored using 15 plate thermometers. These were installed in a rectangular grid at 100 mm from the exposed timber face. The detailed placement and orientation of these is not discussed here but is available in the relevant test reports [15].
3 Results
The temperatures measured with plate thermometers are shown in Fig. 5 for each of the standard furnace and compartment fire experiments. The median values are shown as solid lines, with corresponding 90% confidence intervals shown as shaded areas.
Details and discussion of the compartment fire development for the various ventilation conditions have previously been discussed by Bartlett et al. [23] and McNamee et al. [24]. However, key aspects relevant to the current paper are summarised here.
For all of the ‘natural’ fire scenarios the temperatures in the enclosure measured with plate thermometers exceeded the cellulosic standard temperature time curve (i.e. Standard 1 and 2 in Fig. 5), reaching peak temperatures of approximately 1200°C. The confidence range of the measurements were determined using a bootstrap approach, involving repeated sampling of the data with replacement [25], and thereby generating a multitude of possible measurement distributions which could subsequently be used to construct confidence intervals around a median estimated temperature time curve. Scenario 1 had the shortest burning duration, with the decay phase starting at about 30 min. Scenario 2 began to decay at about 45 min, and Scenario 3 at about 55 min. Scenario 3 also experienced a slower decay than Scenarios 1 and 2 (noting that these readings were obtained using plate thermometers). The structural fire effect(s) of these overall differences in fire development (including versus standard furnace heating conditions) are explored in this paper through structural analysis.
In-depth temperature profiles within the timber are shown in Fig. 6 for four selected positions for each experiment. The measured temperatures at 4 mm and 33 mm in-depth follow similar trends as the temperatures shown in Fig. 5. No clear differences are observed at a depth of 99 mm (i.e. the depth of the third glue line) until about 120 min of fire exposure when the two standard furnace tests show rapidly increasing temperatures; this appears to correspond to a post drying phase of the timber. It also corresponds with a measured average char depth (taken herein as the 300°C isotherm) of about 80–90 mm (see later), and with the time at which deflections significantly increased (see later).
Assessment of the in-depth temperatures in the timber and the charring depths was undertaken using a semi-probabilistic approach. The temperatures were measured at four slab locations in plan (as already described) and these measurement locations can therefore be viewed as samples to estimate the underlying population of an assumed progression of in-depth temperatures within each slab, and thereby the depth of the char front. In addition, each thermocouple in each of the four measurement locations is taken as a sample point for the estimated temperature, and is therefore subject to variation in heating arising from non-uniform exposure and non-uniform material properties across the timber surface.
For a range of reasons it cannot be expected that two thermocouples at the same depth but in two different plan locations will measure precisely the same temperatures at each time step. Therefore any temperature profile fitted against the timber depth, and thus the charring depth approximated from the resulting 300°C isotherm [11, 26] (or any isotherm) represents an estimation of an unknown true temperature distribution within the timber, which is subject to considerable uncertainty. This uncertainty is quantified herein using a bootstrap approach (as explained earlier for the plate thermometer measurements). Using this approach also helps to account for uncertainties arising from a decreasing sensor density of TCs with increasing depth from the fire-exposed timber surface. For the temperature profiles in the current study, smoothing splines were fitted and bootstrapped to the temperature data shown in Fig. 6. Smoothing splines fit a series of splines between data points and are controlled via a smoothing parameter λ, which varies between zero for an essentially linear least square regression fit and unity for a completely smooth fit; herein a smoothing parameter of 0.1 was semi-arbitrarily used. The estimated char depths from the 300°C isotherm, along with their 90% confidence intervals, are shown in Fig. 7. These data compare well with previous data analysis by Mindeguia et al. [27] working from the same data set, but without using this semi-probabilistic approach.
Initially, all three natural fires experienced a more rapid charring rate, likely due to the more rapid increase in fire temperatures (see Fig. 5), with Scenario 3 having a delayed onset due to its longer time to flashover and comparatively slower initial heating rate. Charring was halted in natural fire scenarios 1 and 2 at some point during the decay phase, resulting in ‘final’ char depths of 45 mm and 74 mm, respectively. However, Scenario 3, which had a longer total burning duration but similar peak temperatures, continued to char for longer and eventually reached a char depth of 85 mm, at which point the slab collapsed. It is notable in this context that the standard furnace tests, which experienced continuous heating due to the nature of the standard heating curve, reached char depths of 99 mm and 93 mm before failure, respectively; this suggests that char depth alone (based on a 300°C isotherm) is insufficient (and potentially unconservative) for predicting residual structural performance—particularly in more realistic natural fire scenarios. The different charring depths at failure were primarily caused by the different burning durations, but can also be attributed to varying charring rates throughout the fire durations. Hotter fires caused faster charring progression, as can be seen comparing the Scenario 1 plate thermometer temperatures in Fig. 5 with the corresponding char progression in Fig. 7.
The slabs’ measured midspan deflections are shown in Fig. 8. The deflections for the two standard furnace tests followed similar trends, deviating slightly as failure was reached at 141 min (Standard 1) and 131 min (Standard 2), respectively. In both cases, failure was taken to occur due to a limiting maximum deflection (in this case 475 mm taken from EN 1363-1 [17]) being reached. This is of course a semi-arbitrary failure criterion; however, it allows for quantified comparison of failure times. The limiting rate of deflection (in this case 21 mm/min, again taken from EN 1363-1 [17]) was reached earlier, at 121 min for Standard 1 and 125 min for Standard 2.
The deflection path for Scenario 3 can be seen to deviate significantly earlier than other tests in Fig. 8; this can be related to the progression of heat within this slab. From Fig. 6c) it can be seen that the temperatures at the second glue line in Scenario 3 heat up the fastest, coinciding with the deviation of its deflection path. Increases in temperature at the second glue line mean the third ply (second ply parallel to main stress direction) is heating and being weakened, thereby causing accelerating deflections.
Scenario 2 collapsed 29 h after the onset of heating; this was attributed to continued smouldering within the slab after the fire had effectively burned out within the compartment. This is a notable and important observation; however it is beyond the scope of the current discussion and not discussed further in this paper.
4 Structural Model
A semi-probabilistic structural model was used to predict the reductions in flexural capacity of the slabs based on the measured in-depth temperature data. The timber used in the experimental specimens was strength class C24, meaning that the 5th percentile of the underlying population can be expected to have a modulus of rupture (also known as “bending strength”) of 24 MPa with an expected mean elastic modulus of 11,000 MPa [28]. The Joint Committee on Structural Safety (JCSS) Probabilistic Model Code [29] suggests applying a coefficient of variation (CoV) of 0.25, resulting in a mean modulus of rupture of 36.8 MPa. One thousand randomly generated ambient bending strengths—based on a lognormal distribution—were applied in the subsequent analysis. The elastic modulus was assumed to be similarly distributed, based on a mean of 11,000 MPa and an assumed CoV of 0.13 [29], with a correlation factor of 0.8 [29] between Modulus of Rupture (MoR) and elastic modulus. These are shown in Fig. 9. Perpendicular (to structural span) lamellae were assumed to have 1/30th the ambient temperature elastic modulus of the parallel lamellae [30]. The compressive strength for each simulation run was determined in dependence of the bending strength according to Eq. (1) [29], where for simplicity the correlation coefficient between MoR and compressive strength was taken as unity.
A structural model previously proposed by Wiesner et al. [31], is applied to the experimental data here. The slabs cross sections (analysed as beams per metre width) were discretised into 1000 layers of thickness 0.165 mm and, based on the measured experimental in-depth temperature data, strength and stiffness reductions were applied to the individual layers based on Eurocode [4] mechanical property reduction curves. It should be noted that the Eurocode property reduction curves are only considered valid for timber which is exposed to standard temperature time curves in furnace tests, whereas the true mechanical property reductions will depend on (at least) heating rates, since this will affect the physiochemical structure of the char formed. However, in absence of alternative reduction models and to provide a comparison between furnace and compartment fire tests, these reductions are considered likely to be reasonably applicable also to the natural fire data, for the heating and steady burning phases in particular.
It is necessary to first calculate the position of the neutral plane within the cross section so as to determine which layers are in compression and which are in tension. This necessitates an iterative approach, with an initial estimate of the neutral plane position applied to determine the distribution of the elastic modulus over the entire cross section. The stress distribution can then be approximated, and a new neutral axis depth (and corresponding stress distribution) calculated via Newton–Raphson iterations until axial equilibrium is reached. The iteration procedure is highlighted in Eq. (2), where \(y_{e}\) is the neutral axis location, \(\varepsilon\) is strain, \(E\) is the elastic modulus and \(\kappa\) is the curvature and i denotes the ith-iteration
In the current paper, calculations were performed for 1000 bootstrapped temperature profiles that were randomly matched with each of the mechanical properties shown in Fig. 9 to obtain 1000 evaluations of the bending moment capacity with experimental duration; these could then be used to obtain the estimated median capacity (and associated confidence intervals) that are shown in Fig. 10.
Typical assumptions made in first order cross-sectional capacity analyses were employed herein, namely that (1) plane sections remain plane and (2) shear deformations between lamellae are negligible. The length to depth ratio of 35.8 of the slabs in the experiments summarised in the current paper is greater than the recommended value of 20 above which shear deflections can typically be considered irrelevant [32]. Rolling shear failure is also not considered in the current analysis, since recent research [33] has shown rolling shear to be an unlikely failure mode in fire-exposed CLT elements in simple bending with fire exposure from below.
The cross sectional flexural capacity was then calculated for each time step, using Eq. (3), where \(\sigma_{i}\) is the stress in a given layer, \(A_{i}\) is the layer’s cross sectional area, and \(y_{i}\) is the distance to the neutral axis for each layer in the cross-section.
In the model predictions, failure of the CLT slabs is assessed using two criteria; (1) exceedance of the modulus of rupture by the tension forces in the outer fibres, and (2) exceedance of the ultimate compressive strain, which was set at 0.024 [29] for all simulation scenarios. Fibres exceeding the yield strength were assumed to have yielded, and therefore their compressive stress was set to remain constant at yield strength with increasing compressive strains (i.e. perfectly elastic–plastic mechanical response for timber in compression).
It can be seen in Fig. 10 that, for both of the standard furnace tests, the simulated bending capacity exhibits a rapid drop followed by a slight increase around 50 min. Comparing this with Fig. 7, it appears that this phenomenon arises when the char depth reaches the first glue line. It is therefore likely caused by shifts in the simulated neutral axis due to the sudden change in strength and stiffness between parallel and crosswise orientated (to the main loading direction) fibres in this region. This prediction phenomenon could be prevented through the use of more layers for the simulated cross-section, however this would come with exponentially increasing computational costs, and, since the influence on the overall simulated result is minimal and localised; this refinement is omitted for the current illustration.
For each of the cases modelled here, the structural model gives remarkably accurate predictions of times to failure, i.e. within the error bars for all three tests which failed (two standard and one natural). The two standard furnace tests show very similar flexural capacity reductions; this is to be expected given the similarities in thermal exposure and in-depth temperatures shown in Figs. 5 and 6, and also suggests good repeatability for notionally identical furnace tests on CLT slabs. The median model-predicted failure time for Scenario 3 was 110 min, compared with experimentally observed failure at 108 min (when the char depth was 86 mm). The standard furnace tests, however, significantly exceeded this char depth without collapsing under identical sustained loads.
For comparison, the reduced cross-section method (RCSM), which is recommended in the current version of the EN 1995-1-2 [4] for assessing the fire resistance of structural timber elements, is included purely for illustrative purposes. This method recommends a charring rate of 0.65 mm/min and a zero-strength layer (ZSL) of 7 mm below the char layer, to account for heated but uncharred timber. Any timber below the combined char and ZSL depth is considered to retain its ambient temperature mechanical properties and the capacity of the element can then be calculated in accordance with ambient temperature procedures suggested in EN 1995-1-1 [34]. This calculates the bending capacity based on exceedance of the design bending strength. It must be clearly noted that EN 1995-1-2 is, strictly speaking, not applicable to structural fire design of CLT elements. Nonetheless, the predicted reduction in bending capacity based on this methodology is shown in Fig. 10a) for the two standard fire resistance tests; the predicted failure time for the RCSM is 192 min, resulting in an unconservative prediction. Comparisons with the natural fires in Fig. 10b) are not included, since there is no mechanism by which the RCSM can be credibly adapted for burnout fires with a limited fire duration; and its application to such fires was almost certainly not intended by its developers. This comparison is included only to serve as a reminder to designers that the provisions of the current version of EN 1995-1-2 should not be applied to CLT.
5 Temperature Profiles
The temperature profiles at failure in uncharred timber for all CLT slabs are shown in Fig. 11. For the two experiments that did not fail structurally (i.e. scenarios 1 and 2) the temperature profiles are shown at the moment when the char front reached its deepest position within the CLT cross-section. The majority of simulated failures were caused by tensile rupture, which is in line with expectations for failures of a simply supported bending element with fire exposure to the tension face.
It can be seen that the steady increase in furnace temperature gives a continuous (and relatively steep) temperature gradient at failure for the two standard furnace tests. The confidence intervals of the temperature profiles in Fig. 11 clearly show the influence of the thermocouple placement on the accuracy of resulting assumed in-depth temperature profiles. For the two standard furnace tests the determined temperature profiles become less certain deeper in the cross-section where the resolution of thermocouples reduces, as shown in Fig. 4. For scenarios 2 and 3, the ‘curvy’ estimated temperature profiles and confidence intervals show that variation between different temperature readings exists as the burning duration progresses; this is likely caused by two processes: (1) at deeper depths less thermocouples were used, thereby reducing the resolution, and (2), for longer compartment fires, the in-depth heating of the slabs varied in plan, i.e. the heating and charring depths will vary between the four thermocouple clusters This can be caused by localised char fall off, which will cause uneven thermal boundary conditions across the slab. It is notable that, despite a large confidence range, the spline estimations of the two standard furnace tests do not exhibit a curviness, indicating the more uniform temperature exposure conditions in a furnace compared to a compartment fire with varying ventilation and mixing conditions.
6 Discussion
The three ‘natural’ fire experiments presented herein all had identical fuel loads, were subjected to the same sustained structural loads during fire exposure, and were manufactured by the same supplier from the same timber strength class with the same adhesive type and ply configuration. However, differences in opening geometry, and hence ventilation factor, resulted in considerably different rates of fire growth and durations of pseudo-steady burning, this in turn resulted in significantly different in-depth temperatures in these slabs that were sufficient to result in different structural behaviour, ranging from surviving the full burnout (notwithstanding subsequent smouldering) to collapse at the onset of the decay phase of the fire. These differing responses highlight the importance of understanding the fire dynamics in a compartment fire in a CLT structure, as well as the resulting changes in exposure temperatures.
Of the three ‘natural’ fire scenarios, Scenario 1 had a large opening, corresponding to an opening factor of 4.64 m−0.5 and indicating a more oxygen-rich environment (i.e. tending to fuel controlled). This in turn resulted in a comparatively high proportion of the fuel being able to burn within the compartment (as opposed to in an external fire plume [35]), and resulted in a high internal heat release rate (HRR) and thus a rapid temperature rise. This also resulted in a shorter pseudo-steady burning duration, as the available fuel was able to burn more rapidly due to enhanced re-radiation from the internal burning. Scenario 2 had smaller openings, corresponding to an opening factor of 14.2 m−0.5, indicating a lower availability of oxygen and tending to ventilation controlled. This led to less internal burning (HRR), and resulted in a lower rise in temperatures, less re-radiation to the fuel load, and thus a longer fire pseudo-steady burning duration. Scenario 3 had only one small opening, corresponding to an opening factor of 23.2 m−0.5, indicating even lower oxygen availability and clearly ventilation-controlled burning. This again led to slower temperature increase and further increased the pseudo-steady burning duration; this ultimately meant that the timber was subjected to a longer thermal attack than for the other two scenarios (however at similar peak temperatures), which led to a deeper char depth and enhanced thermal penetration—and ultimately to structural failure during the decay phase. This is potentially important because it means that, for CLT (and other forms of mass timber such as glued laminated timber), the duration of a fire is likely to be more critical for its load bearing capacity than the peak temperatures in the enclosure (for the likely ranges of temperatures). This is intuitive when considering the relatively high thermal inertia and charring behaviour of timber, meaning that temperature increases are concentrated at the hot surface layer with comparatively steep in-depth thermal gradients.
A longer heating phase results in the CLT being exposed to an incident heat flux for a longer duration, thus resulting in increased in-depth heating, and subsequent loss of mechanical properties. The earlier failure of Scenario 3, in comparison to the standard furnace tests, which experienced deeper charring depths but longer failure durations, can thus be expected when the fire dynamics are properly considered. Such consideration is effectively prevented by the current widespread approach of applying normative fire resistance ratings to fire-exposed mass timber structural elements.
The data presented herein also provide compelling evidence that it is important to explicitly consider the decay phase of real fires, rather than relying solely on normative fire resistance ratings for CLT structural elements. After the peak gas phase temperature is reached and the movable fuel load is consumed, the hot surfaces within the compartment will re-radiate, and thus the in-depth temperatures will continue to increase. Even after the room temperature drops, a thermal wave will continue to propagate throughout the member, further increasing the in-depth temperatures for a period which will depend on both the maximum gas phase compartment temperatures and the duration of steady burning. Furthermore, the risk of continued, localised smouldering of the timber means that continued in-depth heating may continue for many hours after the fire appears to have gone out, as was observed for Scenario 2 which collapsed after 29 h due to unseen smouldering. Such considerations are also precluded by the use of normative fire resistance ratings to assess the structural fire response of CLT structural elements.
Both Scenario 1 and Scenario 2 survived fire exposure and decay phases without experiencing structural failure. It can be seen from Fig. 10 that both slabs’ load bearing capacity stabilised as the compartment temperatures reduced and the fire burned out.
Scenario 3 experienced structural failure (i.e. collapse) after 108 min and, as can be seen in Fig. 5, the temperatures at this point remained close to 1000°C. It would thus be premature to label this as a case of auto-extinction, which is also confirmed in Fig. 7 where it can be seen that charring is ongoing at the time of failure in this case. It thus appears that if auto-extinction can be achieved and charring halted, as was observed for Scenarios 1 and 2, then failure in the decay and timber cooling phases of a natural fire for a CLT element in simple bending appear to be unlikely due to redistribution of heat within the CLT (notwithstanding the possible occurrence of ongoing smouldering, which should be considered as a separate issue and is beyond the scope of the current discussion). This is due to the fact that, for slabs in positive bending (i.e. sagging) heat will mostly affect the tension side, and both tensile strength and elastic modulus are generally assumed to be much less affected by elevated temperatures than in compression [4, 36].
Clearly, for a larger initial fuel load or a higher applied load, Scenario 2 could have sustained flaming combustion longer and may have reached a stage where the applied bending moment would have been exceeded. This should be calculated on a case by case basis, and the sectional analysis presented herein shows—and partially validates—how this can be done from a structural fire engineering perspective. This requires that ongoing smouldering, which was observed to cause structural failure for Scenario 2 after 29 hours, can be prevented.
The proposed sectional analysis model, which has not previously been experimentally verified [31], appears able to accurately predict the flexural failures (or lack thereof) for the experiments described in this paper, and such an approach can therefore be seen as a suitable analysis tool to investigate the load bearing capacity of CLT in bending in compartment fires with a decay phase. This analysis model correctly predicted that continuous decay of the structural capacity in one way spanning CLT slabs is limited and unlikely to cause collapse if auto-extinction of a fire can be achieved before structural failure and the progression of the char front has halted. In a previous paper dealing with similar topics, Wiesner et al. [31] had postulated that the fire decay phase may be more critical for compression elements and, given the partial validation of the model herein, the potential for structural collapse in timber compression elements in a fire decay phase should indeed be considered pertinent and to warrant further research.
The RCSM from EN 1995-1-2, which is currently used in practice for the design of cross-laminated timber projects, resulted in unconservative fire resistance predictions. However, it must be reiterated that the RCSM method, in its current form, was not developed, and should not be used, for CLT. Previous researchers have already demonstrated that application of the RCSM to CLT is likely to result in unsafe capacity predictions [37,38,39]. It is expected that future versions of the Eurocode will suggest modifications to the charring rates and the zero strength layers to attempt to provide more conservative simplified design solutions for CLT and other engineered timber products.
The results of the experiments described herein highlight the importance of the ventilation conditions in a compartment with exposed timber surfaces, but also demonstrate the potential to engineer compartments at the design stage based on considerations of the expected burning rates. An early involvement and consultation with structural fire engineers could therefore avoid problems that might arise if the structural fire safety is considered only at later design stages.
7 Conclusion
The experimental work presented herein and the associated structural fire capacity model clearly show the importance of the ventilation conditions in a compartment fire (particularly with a significant area of exposed CLT). Cross-laminated timber slabs were subjected to sustained loads and exposed to both standard furnace heating and to ‘natural’ compartment fires from below using identical fuel loads but with varying ventilation conditions. In two of the three natural fire experiments the CLT slabs structurally survived burnout of the moveable fuel load and achieved auto-extinction. These two tests confirm—as has been shown previously by others [40]—that it is possible to maintain load-bearing, integrity, and insulation requirements for exposed CLT slabs in burnout fires under some conditions. This is notwithstanding the later structural failure of one of these slabs due to in-depth smouldering, which is considered a separate issue and which certainly warrants further research and consideration by designers of CLT buildings.
The presented structural fire model, which is based on a sectional analysis that utilises the measured experimental in-depth temperature distributions in the CLT along with the Eurocode recommended [4] reductions in timber’s mechanical properties on heating to determine the resulting strain distribution at failure, was shown to accurately predict structural capacity during fire in the three cases where failure occurred. The model also correctly predicted no structural failure during the fire growth and decay phases in cases where no failure was observed (again, notwithstanding smouldering). From a structural fire engineering perspective, the results presented herein show that a slow growing fire of longer duration may have more severe effects on the structural load capacity than a shorter but intense fire.
Finally, taken together, the experiments and modelling presented in this paper show that depth of charring cannot be confidently used as the sole means to predict structural capacity of CLT elements when exposed to non-standard (i.e. ‘natural’) fire scenarios. This is due to the fact that loss of mechanical properties of heated timber beneath the char during the heating phase of a fire—and perhaps more importantly during its decay phase—cannot be predicted using such a coarse approximation. This issue should be explicitly considered by structural designers of CLT (and other mass timber) buildings, particularly in cases where structural integrity is required during potential fire evacuation. To achieve this, the further development of heat transfer models for engineered timber products is recommended, to provide fire safety engineers with the necessary tools to model internal temperatures in timber for a range of potential burnout fire scenarios. In addition, education and training should be available for structural fire engineers to explicitly calculate losses in capacity where standard, over-simplified solutions are considered inappropriate.
References
Buchanan AH (2015) Fire resistance of multistorey timber buildings. In: Harada K, Matsuyama K, Himoto K, Nakamura Y, Wakatsuki K (eds) Fire science and technology 2015. Springer, Singapore, pp 9–16
Buchanan AH, Abu AK (2017) Structural design for fire safety. Wiley, New York
Gerhards CC (1982) Effect of moisture content and temperature on the mechanical properties of wood: an analysis of immediate effects. Wood and Fiber Science 14 (1):4–36
CEN (2009) Eurocode 5. Design of timber structures. Part 1-2: General. Structural fire design. European Committee for Standardisation, Brussels
Bartlett AI, Hadden RM, Hidalgo JP, Santamaria S, Wiesner F, Bisby LA, Deeny S, Lane B (2017) Auto-extinction of engineered timber: application to compartment fires with exposed timber surfaces. Fire Saf J 91:407–413. http://doi.org/10.1016/j.firesaf.2017.03.050
Crielaard R, van de Kuilen J-W, Terwel K, Ravenshorst G, Steenbakkers P (2019) Self-extinguishment of cross-laminated timber. Fire Saf J 105:244–260. https://doi.org/10.1016/j.firesaf.2019.01.008
Hadden RM, Bartlett AI, Hidalgo JP, Santamaria S, Wiesner F, Bisby LA, Deeny S, Lane B (2017) Effects of exposed cross laminated timber on compartment fire dynamics. Fire Saf J 91:480–489. https://doi.org/10.1016/j.firesaf.2017.03.074
Emberley R, Do T, Yim J, Torero JL (2017) Critical heat flux and mass loss rate for extinction of flaming combustion of timber. Fire Saf J. https://doi.org/10.1016/j.firesaf.2017.03.008
Gernay T (2019) Fire resistance and burnout resistance of reinforced concrete columns. Fire Saf J 104:67–78. https://doi.org/10.1016/j.firesaf.2019.01.007
Kodur V, Dwaikat M, Fike R (2010) High-temperature properties of steel for fire resistance modeling of structures. J Mater Civ Eng 22(5):423–434. https://doi.org/10.1061/(asce)mt.1943-5533.0000041
White RH, Dietenberger M (2001) Wood products: thermal degradation and fire. In: Encyclopedia of materials: science and technology. Elsevier Science Ltd., pp 9712–9716. https://www.fs.usda.gov/treesearch/pubs/8742
White RH, Woeste FE (2013) Post-fire analysis of solid-sawn heavy timber beams. STRUCTURE magazine, November 2013, pp 38–40. https://www.fs.usda.gov/treesearch/pubs/47253
Hopkin D, Schmid J, Friquin KL (2016) Timber structures subject to non-standard fire exposure—advances and challenges. Paper presented at the world conference on timber engineering, Vienna, Austria
Katakura Y, Kinjo H, Hirashima T, Yusa S, Saito K (2016) Deflection behaviour and load-bearing-period of structural glued laminated timber beams in fire including cooling phase. Paper presented at the structures in fire, Princeton
Epernon Fire Tests Programme (2018). http://www.epernon-fire-tests.eu/
CEN (2014) EN 1365-2 fire resistance tests for load bearing elements. Floors and roofs. European Committee for Standardisation, Brussels
CEN (2012) EN 1363-1 Fire resistance tests. Part 1: general requirements. European Committee for Standardisation, Brussels
CEN (2002) Eurocode 1. Actions on structures. European Committee for Standardisation, Brussels
Thomas PH, Heselden A (1972) Fully-developed fires in single compartments. Fire Research Note
CEN (2002) EN 1991-1-2 Eurocode 1. Actions on structures. General actions. Actions on structures exposed to fire. European Committee for Standardisation, Brussels
Beck JV (1962) Thermocouple temperature disturbances in low conductivity materials. J Heat Transf 84(2):124–131. https://doi.org/10.1115/1.3684310
Fahrni R, Schmid J, Klippel M, Frangi A (2018) Correct temperature measurements in fire exposed wood. In: World conference on timber engineering, Seoul, South Korea
Bartlett AI, McNamee R, Robert F, Bisby LA (2020) Comparative energy analysis from fire resistance tests on combustible versus noncombustible slabs. Fire Mater 44(3):301–310. https://doi.org/10.1002/fam.2760
McNamee R, Zehfuss J, Bartlett A, Bisby L, Heidari M, Robert F (2019) Enclosure fire dynamics with a combustible ceiling. In: Grayson S (ed) Interflam. Interscience Communications, London
Efron B (1979) Bootstrap methods: another look at the jackknife. Ann Stat 7(1):1–26. https://doi.org/10.1214/aos/1176344552
Jönsson R, Pettersson O (1985) Timber structures and fire: a review of the existing state of knowledge and research requirements. Swedish Council for Building Research, Stockholm
Mindeguia JC, Mohaine S, Bisby L, Robert F, McNamee R, Bartlett A (2019) Thermo-mechanical behaviour of cross-laminated timber slabs under standard and natural fires. In: Grayson S (ed) Interflam. Interscience Communications, London
CEN (2009) EN 338 structural timber—strength classes. European Committee for Standardisation, Brussels
Joint Committee on Structural Safety (JCSS) (2001) Probabilistic model code
APA (2018) PRG 320 standard for performance-rated cross-laminated timber. APA-The Engineered Wood Association, Tacoma
Wiesner F, Bisby LA, Bartlett AI, Hidalgo JP, Santamaria S, Deeny S, Hadden RM (2019) Structural capacity in fire of laminated timber elements in compartments with exposed timber surfaces. Eng Struct 179:284–295. https://doi.org/10.1016/j.engstruct.2018.10.084
Blass HJ, Fellmoser P (2004) Design of solid wood panels with cross layers. Paper presented at the 8th world conference on timber engineering,
Wiesner F, Bell D, Chaumont L, Bisby L, Deeny S (2018) Rolling shear capacity of CLT at elevated temperature. In: World conference on timber engineering, Seoul, Republic of Korea
CEN (2014) Eurocode 5. Design of timber structures. Part 1-1: general. Common rules and rules for buildings. European Committee for Standardisation, Brussels
Bartlett A, Law A, Jansson McNamee R, Zehfuss J, Mohaine S, Tessier C, Bisby L (2019) Heat fluxes to a façade resulting from compartment fires with combustible and non-combustible ceilings. In: 3rd international symposium for fire safety of Façades, Paris
König J, Walleij L (2000) Timber frame assemblies exposed to standard and parametric fires: part 2: a design model for standard fire exposure. Institutet för Träteknisk Forskning 0001001:1–76
Schmid J, Klippel M, Just A, Frangi A (2014) Review and analysis of fire resistance tests of timber members in bending, tension and compression with respect to the reduced cross-section method. Fire Saf J 68:81–99
Wiesner F, Randmael F, Wan W, Bisby L, Hadden RM (2017) Structural response of cross-laminated timber compression elements exposed to fire. Fire Saf J 91(Supplement C):56–67. https://doi.org/10.1016/j.firesaf.2017.05.010
Lineham SA, Thomson D, Bartlett AI, Bisby LA, Hadden RM (2016) Structural response of fire-exposed cross-laminated timber beams under sustained loads. Fire Saf J 85:23–34. http://doi.org/10.1016/j.firesaf.2016.08.002
Su J, Lafrance PS, Hoehler MS, Bundy MF (2018) Fire safety challenges of tall wood buildings–phase 2: task 3-cross laminated timber compartment fire tests. NIST, Gaithersburg
Acknowledgements
The authors would like to acknowledge support of Wiesner by the UK Engineering and Physical Sciences Research Council (EPSRC, EP/M508032/1) and Arup. We gratefully acknowledge ongoing support from the project partners: CERIB, Fire Testing Centre; the School of Engineering, The University of Edinburgh; Bordeaux University; Brandskyddslaget AB; the Institute of Building Materials, Concrete Construction and Fire Safety of Technische Universität Braunschweig, Division of Fire Safety; and Liège University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wiesner, F., Bartlett, A., Mohaine, S. et al. Structural Capacity of One-Way Spanning Large-Scale Cross-Laminated Timber Slabs in Standard and Natural Fires. Fire Technol 57, 291–311 (2021). https://doi.org/10.1007/s10694-020-01003-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10694-020-01003-y