Skip to main content
SpringerLink
Log in

A mathematical model to estimate errors associated with closed flux chambers

  • Published:
Environmental Modeling & Assessment Aims and scope Submit manuscript

Abstract

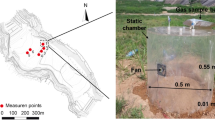
Errors associated with the closed flux chamber technique, used to measure surface emissions from landfills, were investigated by using a combination of numerical modeling and laboratory studies. A transient-state, advective–dispersive–reactive model was developed and used in conjunction with its steady-state version to quantify the errors associated with closed flux chambers. In developing the model, all four major gases, CH4, O2, CO2, and N2, and the oxidation of CH4 to CO2 were considered. Laboratory experiments were conducted on a monolayered as well as a two-layered landfill cover system to calibrate and verify the model. The model was used to develop a plot of the percentage errors associated with closed flux chambers of different dimensions and surface flux rates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Bogner, M. Meadows and P. Czepiel, Soil Use Manag. 13 (1997) 268–277.

    Article  Google Scholar 

  2. P.M. Czepiel, B. Mosher, P.M. Crill and R.C. Harris, J. Geophys. Res. 110(D11) (1996) 16721–16729.

    Article  Google Scholar 

  3. M.D.N. Perera, J.P.A. Hettiaratchi and G. Achari, J. Environ. Eng. Sci. 1 (2002) 451–463.

    Article  CAS  Google Scholar 

  4. R.W. Healy, R.G. Striegl, T.F. Russel, G.L. Hutcinson and G.P. Livingston, Soil Sci. Soc. Am. J. 60 (1996) 740–747.

    Article  CAS  Google Scholar 

  5. W.A. Jury, J. Letley and T. Collins, Soil Sci. Soc. Am. J. 46 (1982) 250–255.

    Article  CAS  Google Scholar 

  6. G.L. Hutchinson and A.R. Mosier, Soil Sci. Soc. Am. J. 45 (1981) 311–315.

    Article  CAS  Google Scholar 

  7. A.D. Matthias, D.N. Yarger and R.S. Weinbeck, Geophys. Res. Lett. 5(9) (1978) 765–768.

    CAS  Google Scholar 

  8. C.W. Fetter, Contaminant Hydrogeology (Macmillan Publishing Company, New York, 1992).

    Google Scholar 

  9. C. Zheng and G.D. Bennett, Applied Contaminant Transport Modeling, 2nd edn. (John Wiley and Sons Inc., New York, 2002).

    Google Scholar 

  10. Y. Jin and W.A. Jury, Soil Sci. Soc. Am. J. 60 (1996) 66–71.

    Article  CAS  Google Scholar 

  11. C.R. Wilke, J. Chem. Eng. Prog. (1950) 46(2) 95–104.

    CAS  Google Scholar 

  12. N.H. Chen and D.F. Othmer, J. Chem. Eng. Data 7(1) (1962) January 37–41.

    Article  Google Scholar 

  13. R.S. Cherry and D.N. Thompson, Biotechnol. Bioeng. 56(3) (1997) November 5 330–339.

    Article  CAS  Google Scholar 

  14. L.A.K. Perera, G. Achari and J.P.A. Hettiaratchi, ASCE J. Environ. Eng. (2002) May 461–471.

  15. S.C. Chapra and R.P. Canale, Numerical Methods for Engineers with Programming and Software Applications, 3rd edn. (WCB/McGraw-Hill, 1998).

  16. L.A.K. Perera, G. Achari and J.P.A. Hettiaratchi, J. Environ. Inform. 4(1) (2004) 11–27.

    Google Scholar 

  17. D.G.M. Senevirathna, G. Achari and J.P.A. Hettiaratchi, Can. J. Civ. Eng. (2006) (in press).

  18. A.D. Matthias, A.M. Blackmer and J.M. Bremner, J. Environ. Qual. 9(2) (1980) 251–255.

    Article  CAS  Google Scholar 

  19. G. Borjesson and B. H. Svensson, Waste Manag. Res. 15 (1997) 33–54.

    Article  Google Scholar 

  20. A.N. Nozhevnikova, A.B. Lifshitz, V.S. Lebdev and G.A. Zavarzin, Chemosphere 26(1–4) (1993) 401–417.

    Article  CAS  Google Scholar 

  21. D.C. Hovde, A.C. Stanton, T.P. Meyers and D.R. Matt, J. Atmos. Chem. 20 (1995) 141–162.

    Article  CAS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, University of Calgary, 2500 University Drive, Calgary, Alberta, T2N 1N4, Canada

    D. G. M. Senevirathna, G. Achari & J. P. A. Hettiaratchi

Authors
  1. D. G. M. Senevirathna
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. Achari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. P. A. Hettiaratchi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. Achari.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Senevirathna, D.G.M., Achari, G. & Hettiaratchi, J.P.A. A mathematical model to estimate errors associated with closed flux chambers. Environ Model Assess 12, 1–11 (2007). https://doi.org/10.1007/s10666-006-9042-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10666-006-9042-x

Keywords

Search

Navigation