Abstract
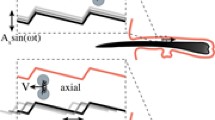
This paper compares the results of a theoretical model with published experimental data investigating the potential use of a drift ratchet as a particle transport device. The drift ratchet of interest here involves the oscillation of a particle-laden fluid through a periodically shaped tube, combined with an exploitation of the Brownian motion of the small particles. Our theoretical results support the experimental evidence that, at these scales, the ratchet effect is not the predominant mechanism for facilitating particle transport. Rather, the tube geometry (but not orientation) and the form of the applied oscillating pressure gradient are the primary characteristics which determine the effectiveness of a device for particle transport. In particular, we find that transport is enhanced in a saw-tooth tube in comparison with a straight, cylindrical tube.







Similar content being viewed by others
References
Rousselet J, Salome L, Ajdari A, Prost J (1994) Directional motion of Brownian particles induced by a periodic asymmetric potential. Nature 370:446–448
Flach S, Yevtushenko O, Zolotaryuk Y (2000) Directed current due to broken time-space symmetry. Phys Rev Lett 84:2358–2361
Matthias S, Müller F (2003) Asymmetric pores in a silicon membrane acting as massively parallel Brownian ratchets. Nature 424:53–57
Mathwig K, Müller f, Gösele U (2011) Particle transport in asymmetrically modulated pores. New J Phys 13:033038
Verleger S, Grimm A, Kreuter C, Ming Tan H, van Kan JA, Erbe A, Scheer E, van der Maarel JRC (2012) A single-channel microparticle sieve based on Brownian ratchets. Lab Chip 12:1238–1241
Bogunovic L, Eichhorn R, Regtmeier J, Anselmetti D, Reimann P (2012) Particle sorting by a structured microfluidic ratchet device with tunable selectivity: theory and experiment. Soft Matter 8:3900–3907
Reimann P (2002) Brownian motors: noisy transport far from equilibrium. Phys Rep 361:57–265
Hänggi P, Bartussek R (1996) Brownian rectifiers: how to convert Brownian motion into directed transport. In: Parisi J, Müller SC, Zimmermann W (eds) Nonlinear physics of complex systems—current status and future trends. Lecture Notes in Physics, vol 476. Springer, Berlin, pp 294–308
Astumian RD (1997) Thermodynamics and kinetics of a Brownian motor. Science 276:917–922
Jülicher F, Ajdari A, Prost J (1997) Modeling molecular motors. Rev Mod Phys 69:1269–1281
Cisne RLC Jr, Vasconcelos TF, Parteli EJR, Andrade JS Jr (2011) Particle transport in flow through a ratchet-like channel. Microfluid Nanofluid 10:543–550
Schindler M, Talkner P, Kostur M, Hänggi P (2007) Accumulating particles at boundaries of a laminar flow. Physica A 385:46–58
Bartussed R, Hänggi P, Kissner JG (1994) Periodically rocked thermal ratchets. Europhys Lett 28:459–464
Kettner C, Reimann P, Hänggi P, Müller F (2000) Drift ratchet. Phys Rev E 61:312–323
Makhnovskii YA, Zitserman VY, Antipov AE (2012) Directed transport of a Brownian particle in a periodically tapered tube. J Exp Theor Phys 142:603–620
Beltrame P, Makhoul M, Joelson M (2016) Deterministic particle transport in a ratchet flow. Phys Rev E 93:012208
Herringer JW, Lester D, Dorrington GE, Rosengarten G, Mitchell JG (2017) Hydrodynamic drift ratchet scalability. AIChE J 63:2358–2366
Islam N, Miklavcic SJ, Bradshaw-Hajek BH, White LR (2017) Convective and diffusive effects on particle transport in asymmetric periodic capillaries. PLoS ONE 12:e0183127
Islam N, Bradshaw-Hajek BH, Miklavcic SJ, White LR (2015) The onset of recirculation flow in periodic capillaries: Geometric effects. Eur J Mech B 53:119–128
Pozrikidis C (1992) Boundary integral and singularity methods for linearised viscous flow. Cambridge University Press, Cambridge
Levich VG (1962) Physicochemical hydrodynamics. Pretence-Hall, Englewood Cliffs
Antipov AE, Barzykin AV, Berezhkovskii AM, Makhnovskii YA, Zitserman VY, Aldoshin SM (2013) Effective diffusion coefficient of a Brownian particle in a periodically expanded conical tube. Phys Rev E 88:054101
Acknowledgements
This work was supported by the Australian Research Council (Grant Number DP1096282). We are grateful to the anonymous referees whose comments helped to improve this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bradshaw-Hajek, B.H., Islam, N., Miklavcic, S.J. et al. Convective and diffusive particle transport in channels of periodic cross-section: comparison with experiment. J Eng Math 111, 1–13 (2018). https://doi.org/10.1007/s10665-017-9950-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-017-9950-6