Abstract
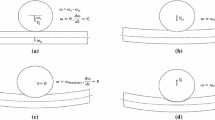
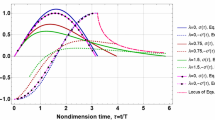
An analytical solution for a low velocity impact between a thin transversely isotropic plate made of a strain-hardening material supported by a rigid substrate and a rigid sphere is presented. One of the novelties of this work is employing a linear strain-hardening model for investigating the indentation phenomenon in the plastic zone, rather than the traditional perfectly plastic model. Another novelty of this work is employing the homotopy perturbation method to derive analytical solutions for the highly nonlinear governing equations of contact. Since it is very important to accurately predict the contact force and its time history, the three stages of the indentation process, i.e., (1) the elastic indentation, (2) the plastic indentation, and (3) the elastic unloading stages, are investigated in detail. Comparison of the present results with results obtained from the iterative numerical time integration method confirms the accuracy and efficiency of the present solution.
Similar content being viewed by others
References
Shariyat M (2006) Automotive body: analysis and design. K. N. Toosi University Press, Tehran
Ollson R (1992) Impact response of orthotropic composite plates predicted form a one-parameter differential equation. AIAA J 30(6): 1587–1596
Yigit AS, Christoforou AP (1994) On the impact of a spherical indenter and an elastic–plastic transversely isotropic half-space. Compos Eng 4(11): 1143–1152
Yigit AS, Christoforou AP (1995) On the impact between a rigid sphere and a thin composite laminate supported by a rigid substrate. Compos Struct 30(2): 169–177
Christoforou AP, Yigit AS (1998) Characterization of impact in composite plates. Compos Struct 43: 5–24
Christoforou AP, Yigit AS (1998) Effect of flexibility on low velocity impact response. J Sound Vib 217: 563–578
Yigit AS, Christoforou AP (2007) Limits of asymptotic solutions in low-velocity impact of composite plates. Compos Struct 81: 568–574
Zheng D, Binienda WK (2007) Effect of permanent indentation on the delamination threshold for small mass impact on plates. Int J Solids Struct 44: 8143–8158
Zheng D, Binienda WK (2009) Semianalytical solution of wave-controlled impact on composite laminates. ASCE J Aero Eng 22(3): 318–323
Christoforou AP, Yigit AS (2009) Scaling of low-velocity impact response in composite structures. Compos Struct 91: 358–365
Swanson SR (2004) Hertzian contact of orthotropic materials. Int J Solids Struct 41: 1945–1959
Swanson SR (2005) Contact deformation and stress in orthotropic plates. Compos A 36: 1421–1429
Chen P, Xiong J, Shen Z (2008) Thickness effect on the contact behavior of a composite laminate indented by a rigid sphere. Mech Mater 40: 183–194
He JH (1999) Homotopy perturbation technique. Comput Methods Appl Mech Eng 178: 257–262
He JH (2000) A coupling method of homotopy technique and perturbation technique for nonlinear problems. Int J Non-Linear Mech 35(1): 37–43
He JH (2004) The homotopy perturbation method for nonlinear oscillators with discontinuities. Appl Math Comput 151: 287–292
Shou D-H (2009) The homotopy perturbation method for nonlinear oscillators. Comput Math Appl 58: 2456–2459
Ganji DD, Alipour MM, Fereidoon AH, Rostamiyan Y (2010) Analytic approach to investigation of fluctuation and frequency of the oscillators with odd and even nonlinearities. Int J Eng 23(1): 41–56
Alipour MM, Shariyat M, Shaban M (2010) A semi-analytical solution for free vibration of variable thickness two-directional-functionally graded plates on elastic foundations. Int J Mech Mater Des 6(4): 293–304
Alipour MM, Shariyat M, Shaban M (2010) A semi-analytical solution for free vibration and modal stress analyses of circular plates resting on two-parameter elastic foundations. J Solid Mech 2(1): 63–78
Christoforou AP (1993) On the contact of a spherical indenter and a thin composite laminate. Compos Struct 28: 77–82
Christoforou AP (2001) Impact dynamics and damage in composite structures. Compos Struct 52(2): 181–188
Christoforou AP, Yigit AS (1995) Transient response of a composite beam subject to elasto-plastic impact. Compos Eng 5(5): 459–470
Conway HD, Lee HC, Bayer RG (1970) The impact between a rigid sphere and a thin layer. J Appl Mech 37: 159–162
Jaffar MJ (1989) Asymptotic behaviour of thin elastic layers bonded and unbonded to a rigid foundation. Int J Mech Sci 31(3): 229–235
Tan TM, Sun CT (1985) Use of statistical indentation laws in the impact analysis of laminated composite plates. J Appl Mech 52: 6–12
Cairns DS, Lagace PA (1987) Thick composite plates subjected to lateral loading. J Appl Mech 54: 611–615
Poe CC Jr, Illg W (1989) Strength of a thick graphite/epoxy rocket motor case after impact by a blunt object. In: Chamis CC (ed) Test methods for design allowables for fibrous composites, vol 2, ASTM STP 1003. ASTM, Philadelphia, pp 150–179
Poe CC Jr (1988) Simulated impact damage in a thick graphite/epoxy laminate using spherical indenters. NASA TM 100539
Bathe KJ (2007) Finite element procedures. Prentice Hall, Englewood Cliffs, NJ
Reddy JN (2005) An introduction to the finite element method, 3rd ed. McGraw-Hill, New York
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Shariyat, M., Ghajar, R. & Alipour, M.M. An analytical solution for a low velocity impact between a rigid sphere and a transversely isotropic strain-hardening plate supported by a rigid substrate. J Eng Math 75, 107–125 (2012). https://doi.org/10.1007/s10665-011-9505-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-011-9505-1