Abstract
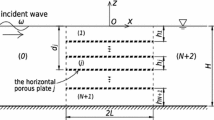
A linear model of waves propagating over a submerged porous breakwater is derived from two coupled boundary-value problems, each of which represents the governing equation in a different medium. The model is similar to the shallow-water equations (SWE), with a damping term proportional to the character of the porous breakwater. Therefore, waves traveling above the breakwater will be absorbed, and the amplitude decreases. The wave propagation passing over the submerged breakwater for monochromatic and solitary waves is analyzed. For monochromatic waves, the numerical solution agrees with the analytical. The amplitude decreases exponentially with respect to the space variable in the region above the breakwater. The reflected wave is also analyzed when the model is combined with a model using the shallow-water equations.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Mei CC, Liu PL-F (1993) Surface waves and coastal dynamics. Annu Rev Fluid Mech 25: 215–240
Yu J, Mei CC (2000) Do longshore bars shelter the shore?. J Fluid Mech 404: 251–268
van Groesen E, Andonowati (2002) Similarities between optic and surface water waves. J Indones Math Soc 8: 1–8
Pudjaprasetya SR, Chendra HD (2009) An optimal dimension of submerged parallel bars as a wave reflector. Bull Malays Math Sci Soc 32: 55–62
Mei CC (1989) The applied dynamics of ocean surface waves. World Scientific, Singapore
Wiryanto LH (2010) Wave propagation over a submerged bar. ITB J Sci 42A: 81–90
Liu PLF, Lin P, Chang KA, Sakakiyama T (1999) Numerical modeling of wave interaction with porous structures. J Waterw Port Coast Ocean Eng 125: 322–330
Huang CJ, Chang HH, Hwung HH (2003) Structure permeability effects on the interaction of a solitary wave and a submerged breakwater. Coast Eng 49: 1–24
Huang CJ, Shen ML, Chang HH (2008) Propagation of a solitary wave over rigid porous beds. Ocean Eng 35: 1194–1202
Hsiao SC, Liu PLF, Chen Y (2002) Nonlinear water waves propagating over a permeable bed. Proc R Soc Lond A 458: 1291–1322
Solitt CK, Cross RH (1972) Wave transmission through permeable breakwaters. In: Proceedings of 13th international conference on Coastal engineering, Vancouver, pp 1837–1846
Madsen OS (1974) Wave transmission through porous structures. J Waterw Harbors Coast Eng 100: 169–188
Rojanakamthorn S, Isobe M, Watanabe A (1989) A mathematical model of wave transformation over a submerged breakwater. Coast Eng Jpn 31: 209–234
Dalrymple RA, Losada MA, Martin PA (1991) Reflection and transmission from porous structures under oblique wave attack. J Fluid Mech 224: 625–644
Tsai CP, Chen HB, Lee FC (2006) Wave transformation over submerged permeable breakwater on porous bottom. Ocean Eng 33: 1623–1643
Tsai CP, Chen HB, Jeng DS (2009) Wave attenuation over a rigid porous medium on a sandy seabed. J Eng Mech 135: 1295–1305
Wiryanto LH (2010) Unsteady waves generated by flow over a porous layer. Int J Appl Math (accepted)
Mizumura K (1998) Free surface flow over permeable wavy bed. J Hydraul Eng 124: 955–962
Wiryanto LH, Anwarus S (2009) Monochromatic waves over permeable bed. In: Proceedings of 5th Asian Mathematical Conference, Kuala Lumpur, Malaysia, pp 617–622
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wiryanto, L.H. Wave propagation passing over a submerged porous breakwater. J Eng Math 70, 129–136 (2011). https://doi.org/10.1007/s10665-010-9419-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-010-9419-3