Skip to main content
SpringerLink
Log in

The motion of the free-surface separation point during the initial stage of horizontal impulsive displacement of a floating circular cylinder

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

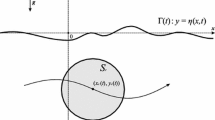
The initial stage of unsteady two-dimensional flow caused by the impulsive horizontal motion of a floating circular cylinder is investigated by using methods of asymptotic analysis. Initially the cylinder is half-submerged and the liquid free surface is flat and horizontal. The liquid is of infinite depth. Then the cylinder suddenly starts to move horizontally with a speed given as a function of time. The liquid is assumed ideal and incompressible and its flow potential. The initial flow is provided by pressure-impulse theory, with an account of a possible separation of the liquid free surface from the trailing face of the rigid surface of the cylinder. The initial position of the separation point on the surface of the moving body is determined by using the condition that the fluid velocity is finite at the separation point (Kutta condition). The motion of the separation point along the surface of the cylinder is numerically determined with the help of the second-order outer solution of the problem and the Kutta condition at the moving separation point. It is shown that the length of the wetted part of the cylinder surface increases at a rate proportional to the speed of the cylinder. The speed of the separation point depends on the Froude number. The pressure on the wetted part of the cylinder can be below the atmospheric pressure for relatively high speed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Sedov LI (1965) Two-dimensional problems of hydrodynamics and aerodynamics. Interscience Publications, New York

    Google Scholar 

  2. Kudryavtseva NA (1960) Horizontal impact of a floating ellipse on an incompressible fluid. Prikl Mat Mekh 24: 258–261

    Google Scholar 

  3. Korchagin VS (1978) Separation impact on a cylinder semi-submerged in a fluid. Izv Sev-Kavkaz Nauchn Tsentr Vyssh Shkoly Estestv Nauki 4: 25–27

    Google Scholar 

  4. Korchagin VS (1989) Separation impact of a body on an incompressible fluid. Izv Sev-Kavkaz Nauchn Tsentr Vyssh Shkoly Estestv Nauki 3: 30–33

    Google Scholar 

  5. Dvorak AV, Teselkin DA (1986) Numerical solution of two-dimensional problems of pulsed motion of floating bodies. Zh Vychisl Mat Mat Fiz 26(1): 144–150

    Google Scholar 

  6. Yudovich VI (2005) Unique solvability of the problem of separation impact of a solid on an inhomogeneous fluid. Vladikavkaz Mat Zh 7(3): 79–91

    MathSciNet  Google Scholar 

  7. Norkin MV (2005) Methods of solving nonlinear problems of hydrodynamic impact in bounded regions. Fluid Dyn 40(4): 623–634

    Article  MathSciNet  ADS  MATH  Google Scholar 

  8. Lions JL (1971) Optimal control of systems governed by partial differential equations. Springer, New York

    MATH  Google Scholar 

  9. Norkin MV (2008) Separating impact on an elliptic cylinder floating on the surface of an ideal incompressible finite-depth. Fluid Dyn 43(1): 105–117

    Article  MathSciNet  ADS  MATH  Google Scholar 

  10. Norkin MV (2009) Separation impact of an elliptic cylinder floating on the surface of an inhomogeneous incompressible fluid. Izvestia Vusov Severo-Kavkazskii Region, Special Issue “Actual problems of mathematical hydrodynamics”. Nat Sci 168–173

  11. Norkin MV (2009) Separation impact of a circular disk floating on the surface of an ideal incompressible fluid of infinite depth. J Appl Mech Tech Phys 50(4): 607–616

    Article  MathSciNet  ADS  Google Scholar 

  12. Galanov BA (1985) The method of boundary equations of the Hammerstein-type for contact problems of the theory of elasticity when the regions of contact are not known. J Appl Math Mech 49: 634–640

    Article  MathSciNet  ADS  MATH  Google Scholar 

  13. Galanov BA (1987) Nonlinear boundary equations for contact problems of the elasticity theory. Dokl Acad Nauk SSSR 296: 812–815

    MathSciNet  Google Scholar 

  14. Aleksandrov VM, Pozharskii DA (1998) Nonclassical three dimensional problems of mechanics of contact interaction between elastic bodies. Faktorial, Moscow [in Russian]

  15. Aleksandrov VM, Chebakov MI (2004) Analytical methods in contact problems of the elasticity theory. Fizmatlit, Moscow [in Russian]

  16. Korobkin AA (1982) Formulation of penetration problem as a variational inequality. Dyn Sploshnoi Sredy 58: 73–79

    MATH  Google Scholar 

  17. Gazzola T, Korobkin AA, Malenica S (2006) Hydro-elastic Wagner impact using variational inequalities. In: Proceedings of 21th international workshop on water waves and floating bodies, Loughborough, UK, pp 57–60

  18. Korobkin AA (1993) Low-pressure zones under a liquid–solid impact. In: Blake JR, Boulton-Stone JM, Thomas NH (eds) Bubble dynamics and interface phenomena: proceedings of the IUTAM symposium, held in Birmingham, UK, 6–9 September, 1993. Kluwer, Dordrecht, pp 375–381

  19. Korobkin AA (2003) Cavitation in liquid impact problem. In: Proceedings of the 5th international congress on cavitation, Osaka, Japan, 6 pp

  20. Needham DJ, Billingham J, King AC (2007) The initial development of a jet caused by fluid, body and free-surface interaction. Part 2. An impulsively moved plate. J Fluid Mech 578: 67–84

    Article  MathSciNet  ADS  MATH  Google Scholar 

  21. Korobkin AA, Iafrati A (2005) Hydrodynamic loads during initial stage of floating body impact. J Fluids Struct 21: 413–427

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Southern Federal University, Rostov-on-Don, Russia

    Michail Norkin

  2. School of Mathematics, University of East Anglia, Norwich, UK

    Alexander Korobkin

Authors
  1. Michail Norkin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alexander Korobkin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alexander Korobkin.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Norkin, M., Korobkin, A. The motion of the free-surface separation point during the initial stage of horizontal impulsive displacement of a floating circular cylinder. J Eng Math 70, 239–254 (2011). https://doi.org/10.1007/s10665-010-9416-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-010-9416-6

Keywords

Search

Navigation