Abstract
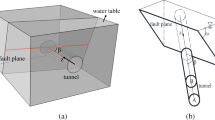
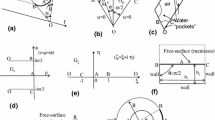
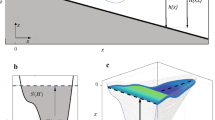
An explicit analytical solution to the problem of steady Darcian seepage into a constant-head subsurface gallery (a straight line segment) placed in a homogeneous rock under a leaky layer of silt deposited in a reservoir is obtained. The third-type boundary condition (linear relation between the head and normal component of the Darcian velocity) along the interface between sediments and rock is tackled by the Verigin function, which satisfies the mixed boundary-value problem conditions in a domain obtained by a conformal mapping of the physical plane (quadrangle) onto an auxiliary plane. This function has three integrable singularities and, unlike Verigin’s attempt to construct the second conformal mapping, we use a Signorini-type integral representation. The gallery flow rate is plotted as a function of the gallery size, location under the leaky layer, and the leakage factor, which combines the hydraulic conductivities of the rock and silt, the difference in hydraulic head between the reservoir bottom above the leaky layer and the gallery contour and the silt thickness.
Similar content being viewed by others
References
Rowe RK, Quigley RM and Booker JR (1995). Clayey barrier systems for waste disposal facilities. Chapman & Hall, London
Strack ODL (1989). Groundwater mechanics. Prentice Hall, Englewood Hills
Kacimov AR (2008). Maximisation of water storage in back-filled and lined channels and dimples subject to evaporation and leakage. J Irrigation Drainage ASCE 134: 101–106
Prathapar S, Perret J, Seckler D (2004) A new approach to bypass silt deposition in recharge dams. In: Proceedings of Regional Workshop on Management of Aquifer Recharge and Water Harvesting in Arid and Semi-arid Regions of Asia. Yazd, Iran, pp 69–79
Voutchkov N (2005). Well design and construction. In: Lehr, J (eds) Water encyclopedia. V.4 groundwater, pp 87–91. Wiley, Hoboken, New Jersey
Polubarinova-Kochina PYa (1977). Theory of groundwater movement. Nauka, Moscow (in Russian)
Cedergren HR (1989). Seepage, drainage and flow nets. Wiley, New York
Romanova EYa (1956). The influence of a crack in the upstream apron on seepage under a dam. In: Mikhailov, KA (eds) Problems of calculation of seepage through hydraulic structures, vol 23. GILSA, Moscow (in Russian)
Hunt B and Massmann J (2000). Vapor flow to trench in leaky aquifer. J Environ Eng ASCE 126: 375–381
Bakker M (1999). Simulating groundwater flow in multi-aquifer systems with analytical and numerical dupuit-models. J Hydrol 222: 55–64
Bruggeman GA and Veling EJM (2005). Nonmonotonic trajectories to a partially penetrating well in a semiconfined aquifer. Water Resour Res 42 WO2501. doi: 20.1029/2005WR003951
Anderson EI (2000). The method of images for leaky boundaries. Adv Water Resour 23: 461–474
Verigin NN (1949). On calculation of subsurface water uptake in conditions of 2-d groundwater movement. DAN SSSR 64: 183–186 (In Russian)
Kacimov AR and Obnosov YuV (2000). Conduction through a grooved surface and sierpinsky fractals. Int J Heat Mass Transfer 43: 623–628
Anderson EI (2003). An approximation for leaky boundaries in groundwater flow. J Hydrol 274: 160–175
Kacimov AR and Obnosov YuV (2001). Semipermeable boundaries and heterogeneities: modeling by singularities. J Hydrol Eng ASCE 6: 217–224
Malov YuI, Martinson LK and Pavlov KB (1974). Solution of some mixed boundary-value heat conduction problems. J Eng Phys Thermophys 27: 335–340
Minasyan RS (1952). On a mixed boundary-value problem for the laplace equation in a rectangle. Prikl Mat Mekh 16: 291–304 (In Russian)
Van Der Veer P (1978). Exact solutions for two-dimensional groundwater flow problems involving a semi-pervious boundary. J Hydrol 37: 159–168
Van Der Veer P (1994). Exact solutions for two-dimensional groundwater flow in a semiconfined aquifer. J Hydrol 156: 91–99
Bruggeman GA (1999). Analytical solutions of geohydrological problems. Elsevier, Amsterdam
Obnosov YuV (1981). Solution of a mixed boundary-value problem in the theory of analytic functions. Izv VUZ Mat (Soviet Mathematics) 10: 75–79
Muscat M (1946). The flow of homogeneous fluids through porous media. I.W. Edwards Inc, Ann Arbor
Wolfram S (1991) Mathematica: A system for doing mathematics by computer. Addison-Wesley
Muscat M (1949). Physical principles of oil production. McGraw Hill, New York
Gakhov FD (1977) Boundary value problems, 3rd edn. Nauka, Moscow, (In Russian). Engl. translation of the 2nd edn. (1966) Addison Wesley, New York
Youngs EG, Kacimov AR and Obnosov YuV (2004). Water exclusion from tunnel cavities located in the saturated capillary fringe with uniform precipitation flowing to a water bearing substratum. Adv Water Resour 27: 237–243
Strakhov IA (1972). Heat transfer problem for a semi-infinite body heated by thin parallel plates. J Eng Phys Thermophys 23: 331–338
Goldstejn RV and Entov VM (1994). Qualitative methods in continuum mechanics. Wiley, New York
Carslaw HS and Jaeger JC (1959). Conduction of heat in solids. Oxford University Press, Oxford
Kacimov AR and Obnosov YuV (2006). Strip-focused phreatic surface flow driven by evaporation: analytical solution by the Riesenkampf function. Adv Water Resour 29: 1565–1571. doi: 10.1016/j.advwatres.2006.01.004
Kacimov AR and Obnosov YuV (2008). Analytical solution to 2D problem for an anticline-diverted brine flow with a floating hydrocarbon trap. Transp Porous Media 71(1): 39–52. doi: 10.1007/s11242-007-9110-y
Kacimov AR, Marketz F, Pervez T (2008) Optimal placement of a wellbore seal impeding seepage from a tilted fracture. Appl Mathemat Model (Elsevier) (in press)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kacimov, A.R., Obnosov, Y.V. Leaky-layer seepage: the Verigin function revisited. J Eng Math 62, 345–354 (2008). https://doi.org/10.1007/s10665-008-9223-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-008-9223-5