Abstract
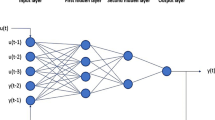
The paper presents the screening of various feedforward neural networks (FANN) and wavelet–feedforward neural networks (WFANN) applied to time series of ground-level ozone (O3), nitrogen dioxide (NO2), and particulate matter (PM10 and PM2.5 fractions) recorded at four monitoring stations located in various urban areas of Romania, to identify common configurations with optimal generalization performance. Two distinct model runs were performed as follows: data processing using hourly-recorded time series of airborne pollutants during cold months (O3, NO2, and PM10), when residential heating increases the local emissions, and data processing using 24-h daily averaged concentrations (PM2.5) recorded between 2009 and 2012. Dataset variability was assessed using statistical analysis. Time series were passed through various FANNs. Each time series was decomposed in four time-scale components using three-level wavelets, which have been passed also through FANN, and recomposed into a single time series. The agreement between observed and modelled output was evaluated based on the statistical significance (r coefficient and correlation between errors and data). Daubechies db3 wavelet–Rprop FANN (6-4-1) utilization gave positive results for O3 time series optimizing the exclusive use of the FANN for hourly-recorded time series. NO2 was difficult to model due to time series specificity, but wavelet integration improved FANN performances. Daubechies db3 wavelet did not improve the FANN outputs for PM10 time series. Both models (FANN/WFANN) overestimated PM2.5 forecasted values in the last quarter of time series. A potential improvement of the forecasted values could be the integration of a smoothing algorithm to adjust the PM2.5 model outputs.





Similar content being viewed by others
References
Caselli, M., Trizio, L., de Gennaro, G., & Ielpo, P. (2009). A simple feedforward neural network for the PM10 forecasting: comparison with a radial basis function network and a multivariate linear regression model. Water, Air, & Soil Pollution, 201(1-4), 365–377.
Dimitriou, K., Kassomenos, P. A., & Paschalidou, A. K. (2013). Assessing air quality with regards to its effect on human health in the European Union through air quality indices. Ecological Indicators, 27, 108–115.
Dunea, D., Oprea, M., & Lungu, E. (2008). Comparing statistical and neural network approaches for urban air pollution time series analysis. In L. Bruzzone (Ed.), MIC ‘08 Proceedings of the 27th IASTED International Conference on Modelling, Identification and Control (pp. 93–98). Anaheim: Acta Press.
Dunea, D., Pohoata, A., & Lungu, E. (2011). Fuzzy inference systems for estimation of air quality index. ROMAI Journal, 7(2), 63–70.
Dunea, D., Iordache, S., Oprea, M., Savu, T., Pohoata, A., & Lungu, E. (2014). A relational database structure for linking air pollution levels with children’s respiratory illnesses. Bulletin UASVM Agriculture Cluj-Napoca, 71(2), 205–213.
EC, European Commission (2013). Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the regions, A Clean Air Programme for Europe, http://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=COM:2013:0918:FIN:EN:PDF. Accessed 28 February 2015.
EEA, European Environment Agency (2013). Air pollution fact sheet 2013—Romania, http://www.eea.europa.eu/themes/air/air-pollution-country-fact-sheets/romania-air-pollutant-emissions-country-factsheet. Accessed 28 February 2015.
EEA, European Environment Agency (2014). Air quality in Europe—2014 report, http://www.eea.europa.eu/publications/air-quality-in-europe-2014. Accessed 28 February 2015.
Foresee, F.D., & Hagan, M.T. (1997). Gauss-Newton approximation to Bayesian regularization. Proceedings of the 1997 International Joint Conference on Neural Networks, 1930–1935.
Guo, X. (2010). Learning gradients via an early stopping gradient descent method. Journal of Approximation Theory, 162(11), 1919–1944.
Hajek, P., & Olej, V. (2009). Air quality indices and their modelling by hierarchical Fuzzy Inference Systems. WSEAS Transactions on Environment and Development, 5(10), 661–672.
Han, J., & Kamber, M. (2006). Data mining: concepts and techniques. San Francisco: Elsevier Inc.-Morgan Kaufman.
Henschel, S., Atkinson, R., Zeka, A., Le Tertre, A., Analitis, A., Katsouyanni, K., Chanel, O., Pascal, M., Forsberg, B., Medina, S., & Goodman, P. G. (2012). Air pollution interventions and their impact on public health. International Journal of Public Health, 57, 757–768.
IARC, International Agency for Research on Cancer (2013). Outdoor air pollution a leading environmental cause of cancer deaths. http://www.iarc.fr/en/media-centre/iarcnews/pdf/pr221_E.pdf . Accessed 28 February 2015.
Iordache, Ş., & Dunea, D. (2013). Cross-spectrum analysis applied to air pollution time series from several urban areas of Romania. Environmental Engineering and Management Journal, 12(4), 677–684.
Jin, T., Gao, J., Fu, L., Ai, Y., & Xu, X. (2012). An evaluation of improvements in the air quality of Beijing arising from the use of new vehicle emission standards. Environmental Monitoring and Assessment, 184(4), 2151–2159.
Liu, H.-Y., Skjetne, E., & Kobernus, M. (2013). Mobile phone tracking: in support of modelling traffic-related air pollution contribution to individual exposure and its implications for public health impact assessment. Environmental Health, 12, 93.
Lu, W. Z., Wang, W. J., Wang, X. K., Xu, Z. B., & Leung, A. Y. T. (2003). Using improved neural network model to analyze RSP, NOx and NO2 levels in urban air in Mong Kok, Hong Kong. Environmental Monitoring and Assessment, 87(3), 235–254.
Lungu, E., Oprea, M., & Dunea, D. (2008). An application of artificial neural networks in environ-mental pollution forecasting. In A. Gammerman (Ed.), AIA ‘08 Proceedings of the 26th IASTED International Conference on Artificial Intelligence and Applications (pp. 187–193). Anaheim: Acta Press.
Misiti, M., Misiti, Y., Oppenheim, G., & Poggi, J.-M. (2013). Matlab Wavelet Toolbox™ User’s Guide. The MathWorks, Inc.
Modarres, R., & Khosravi Dehkordi, A. (2005). Daily air pollution time series analysis of Isfahan City. International Journal of Environmental Science and Technology, 2(3), 259–267.
Moustris, K. P., Ziomas, I. C., & Paliatsos, A. G. (2010). 3-Day-ahead forecasting of regional pollution index for the pollutants NO2, CO, SO2, and O3 using artificial neural networks in Athens, Greece. Water, Air, & Soil Pollution, 209(1-4), 29–43.
Neuberger, M., Schimek, M. G., Horak, F., Jr., Moshammer, H., Kundi, M., Frischer, T., Gomiscek, B., Puxbaum, H., Hauck, H., & AUPHEP-Team. (2004). Acute effects of particulate matter on respiratory diseases, symptoms and functions: epidemiological results of the Austrian Project on Health Effects of Particulate Matter (AUPHEP). Atmospheric Environment, 38, 3971–3981.
Nunnari, G., Dorling, S., Schlink, U., Cawley, G., Foxall, R., & Chatterton, T. (2004). Modelling SO2 concentration at a point with statistical approaches. Environmental Modelling & Software, 19(10), 887–905.
Oprea, M. (2012). INTELLEnvQ-Air: an intelligent system for air quality analysis in urban regions. International Journal of Artificial Intelligence, 9(A12), 106–122.
Organisation for Economic Co-operation and Development—OECD (2012). The OECD Environment Outlook 2050: The Consequences of Inaction, http://www.oecd.org/environment/oecdenvironmentaloutlookto2050theconsequencesofinaction.htm. Accessed 28 February 2015.
Prakash, A., Kumar, U., Kumar, K., & Jain, V. K. (2011). A wavelet-based neural network model to predict ambient air pollutants’ concentration. Environmental Modeling & Assessment, 16(5), 503–517.
Rahman, S. M., Khondaker, A. N., & Abdel-Aal, R. (2012). Self organizing ozone model for Empty Quarter of Saudi Arabia: group method data handling based modeling approach. Atmospheric Environment, 59, 398–407.
Riga, M., Tzima, F., Karatzas, K., & Mitkas, P. (2009). Development and evaluation of data mining models for air quality prediction in Athens, Greece. Environmental Science and Engineering, 2009, 331–344.
RNMCA, Romanian Air Quality Monitoring National Network (2015). http://www.calitateaer.ro. Accessed on 28 February 2015.
Siwek, K., & Osowski, S. (2012). Improving the accuracy of prediction of PM10 pollution by the wavelet transformation and an ensemble of neural predictors. Engineering Applications of Artificial Intelligence, 25, 1246–1258.
Sotomayor-Olmedo, A., Aceves-Fernández, M. A., Gorrostieta-Hurtado, E., Pedraza-Ortega, C., Ramos-Arreguín, J. M., & Vargas-Soto, J. E. (2013). Forecast urban air pollution in Mexico City by using support vector machines: a kernel performance approach. International Journal of Intelligence Science, 3, 126–135.
Srivastava, N., Geoffrey, H., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. (2014). Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 15, 1929–1958.
Stolojescu, C., Railean, I., Moga, S., Lenca, Ph., & Isar, A. (2010). A wavelet based prediction method for time series, Proceedings of Stochastic Modeling Techniques and Data Analysis (SMTDA2010) International Conference, Chania, Greece.
Tetko, I. V., Livingstone, D. J., & Luik, A. I. (1995). Neural network studies. 1. Comparison of overfitting and overtraining. Journal of Chemical Information and Modeling, 35(5), 826–833.
Turias, I. J., González, F. J., Martin, M. L., & Galindo, P. L. (2008). Prediction models of CO, SPM and SO2 concentrations in the Campo de Gibraltar Region, Spain: a multiple comparison strategy. Environmental Monitoring and Assessment, 143(1-3), 131–146.
WHO, World Health Organization (2014). Ambient (outdoor) air quality and health—fact sheet no. 313, Updated March 2014, http://www.who.int/mediacentre/factsheets/fs313/en. Accessed 28 February 2015.
Wu, E. M.-Y., & Kuo, S.-L. (2012). Air quality time series based GARCH model analyses of air quality information for a total quantity control district. Aerosol and Air Quality Research, 12, 331–343.
Zainuddin, Z., & Pauline, O. (2011). Modified wavelet neural network in function approximation and its application in prediction of time-series pollution data. Applied Soft Computing, 11, 4866–4874.
Zhang, Y., Seigneur, C., Bocquet, M., Mallet, V., & Baklanov, A. (2012). Real-time air quality forecasting, part I: history, techniques, and current status. Atmospheric Environment, 60, 632–655.
Zhao, Y., & Hasan, Y. A. (2013). Comparison of three classification algorithms for predicting PM2.5 in Hong Kong rural area. Journal of Asian Scientific Research, 3(7), 715–728.
Zolghadri, A., & Henry, D. (2004). Minimax statistical models for air pollution time series. Application to ozone time series data measured in Bordeaux. Environmental Monitoring and Assessment, 98(1-3), 275–294.
Acknowledgments
The research leading to these results has received funding from European Economic Area Financial Mechanism 2009–2014 under the project ROKIDAIR “Towards a better protection of children against air pollution threats in the urban areas of Romania” contract no. 20SEE/30.06.2014.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Dunea, D., Pohoata, A. & Iordache, S. Using wavelet–feedforward neural networks to improve air pollution forecasting in urban environments. Environ Monit Assess 187, 477 (2015). https://doi.org/10.1007/s10661-015-4697-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10661-015-4697-x