Abstract
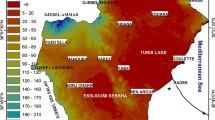
Giving an appropriate weight to each sampling point is essential to global mean estimation. The objective of this paper was to develop a global mean estimation method with preferential samples. The procedure for this estimation method was to first zone the study area based on self-organizing dual-zoning method and then to estimate the mean according to stratified sampling method. In this method, spreading of points in both feature and geographical space is considered. The method is tested in a case study on the metal Mn concentrations in Jilin provinces of China. Six sample patterns are selected to estimate the global mean and compared with the global mean calculated by direct arithmetic mean method, polygon method, and cell method. The results show that the proposed method produces more accurate and stable mean estimates under different feature deviation index (FDI) values and sample sizes. The relative errors of the global mean calculated by the proposed method are from 0.14 to 1.47 % and they are the largest (4.83–8.84 %) by direct arithmetic mean method. At the same time, the mean results calculated by the other three methods are sensitive to the FDI values and sample sizes.







Similar content being viewed by others
References
Botta-Dukát, Z., Kovács-Láng, E., Rédei, T., Kertész, M., & Garadnai, J. (2007). Statistical and biological consequences of preferential sampling in phytosociology: theoretical considerations and a case study. Folia Geobotanica, 42(2), 141–152.
Deutsch, C. (1989). DECLUS: a FORTRAN 77 program for determining optimum spatial declustering weights. Computers & Geosciences, 15(3), 325–332.
Diggle, P. J., Menezes, R., & Su, T. L. (2010). Geostatistical inference under preferential sampling. Journal of the Royal Statistical Society: Series C (Applied Statistics), 59(2), 191–232.
Dubois, G., & Saisana, M. (2002). Optimizing spatial declustering weights—comparison of methods (pp. 479–484). Berlin-Germany: In Proceedings of the Annual Conference of the International Association for Mathematical Geology.
Goovaerts, P. (1997). Geostatistics for natural resources evaluation (pp. 393–395). New York: Oxford University Press.
Gupta, S., & Shabbir, J. (2007). On the use of transformed auxiliary variables in estimating population mean by using two auxiliary variables. Journal of Statistical Planning and Inference, 137(5), 1606–1611.
Isaaks, E. H., & Srivastava, R. M., 1989. Applied geostatistics .Oxford University Press, 561pp.
Jiao, L., Liu, Y., & Zou, B. (2011). Self-organizing dual clustering considering spatial analysis and hybrid distance measures. Science China Earth Sciences, 54(8), 1268–1278.
Journel, A. G. (1983). Nonparametric estimation of spatial distributions. Journal of the International Association for Mathematical Geology, 15(3), 445–468.
Kamiran, F., & Calders, T., 2010. Classification with no discrimination by preferential sampling. In Proc. Benelearn.
Kohonen, T. (1990). The self-organizing map. Proceedings of the IEEE, 78(9), 1464–1480.
Li, L., Wang, J., Cao, Z., & Zhong, E. (2008). An information-fusion method to identify pattern of spatial heterogeneity for improving the accuracy of estimation. Stochastic Environmental Research and Risk Assessment, 22(6), 689–704.
Lin, C. R., Liu, K. H., & Chen, M. S. (2005). Dual clustering: integrating data clustering over optimization and constraint domains. Knowledge and Data Engineering, IEEE Transactions on, 17(5), 628–637.
Menezes, R., 2009. Clustering and preferential sampling, two distinct issues in geostatistics. In XVII Annual Congress of the Portuguese Society of Statistics.
Merckx, B., Steyaert, M., Vanreusel, A., Vincx, M., & Vanaverbeke, J. (2011). Null models reveal preferential sampling, spatial autocorrelation and overfitting in habitat suitability modelling. Ecological Modelling, 222(3), 588–597.
Michalcová, D., Lvončík, S., Chytrý, M., & Hájek, O. (2011). Bias in vegetation databases? A comparison of stratified-random and preferential sampling. Journal of Vegetation Science, 22(2), 281–291.
Olea, R. A. (2007). Declustering of clustered preferential sampling for histogram and semivariogram inference. Mathematical Geology, 39(5), 453–467.
Rao, T. J. (1981). On a class of almost unbiased ratio estimators. Annals of the Institute of Statistical Mathematics, 33(1), 225–231.
Shabbir, J., & Yaab, M. Z. (2003). Improvement over transformed auxiliary variable in estimating the finite population mean. Biometrical Journal, 45(6), 723–729.
Tai, C. H., Dai, B. R., & Chen, M. S. (2007). Incremental clustering in geography and optimization spaces. In Advances in Knowledge Discovery and Data Mining (pp. 272–283). Berlin Heidelberg: Springer.
Thiessen, A. H. (1911). Precipitation averages for large areas. Monthly Weather Review, 39(7), 1082–1089.
Wang, J. F., Christakos, G., & Hu, M. G. (2009). Modeling spatial means of surfaces with stratified nonhomogeneity. Geoscience and Remote Sensing, IEEE Transactions on, 7(12), 4167–4174.
Wang, J., Haining, R., & Cao, Z. (2010). Sample surveying to estimate the mean of a heterogeneous surface: reducing the error variance through zoning. International Journal of Geographical Information Science, 24(4), 523–543.
Acknowledgments
This study was funded by the National Natural Science Foundation of China (No. 40971237 and No. 41201173) and the Open Fund of National Engineering Research Center for Information Technology in Agriculture (No. KF2012N08-055).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pan, Y., Ren, X., Gao, B. et al. Global mean estimation using a self-organizing dual-zoning method for preferential sampling. Environ Monit Assess 187, 121 (2015). https://doi.org/10.1007/s10661-015-4356-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10661-015-4356-2