Abstract
We consider the volumetric-isochoric split in planar isotropic hyperelasticity and give a precise analysis of rank-one convexity criteria for this case, showing that the Legendre-Hadamard ellipticity condition separates and simplifies in a suitable sense. Starting from the classical two-dimensional criterion by Knowles and Sternberg, we can reduce the conditions for rank-one convexity to a family of one-dimensional coupled differential inequalities. In particular, this allows us to derive a simple rank-one convexity classification for generalized Hadamard energies of the type \(W(F)=\frac{\mu }{2} \hspace{0.07em} \frac{\lVert F \rVert ^{2}}{\det F}+f(\det F)\); such an energy is rank-one convex if and only if the function \(f\) is convex.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Undoubtedly, one of the most important constitutive requirements in nonlinear elasticity is the rank-one convexity of the elastic energy \(W\colon \operatorname{GL}^{\!+}(n)\to \mathbb{R}\). For \(C^{2}\)-smooth energy functions, rank-one convexity is nothing else than the Legendre-Hadamard ellipticity condition expressing the ellipticity of the Euler-Lagrange equations
Thus, rank-one convexity for smooth energies amounts to the requirement
for all \(F\in \operatorname{GL}^{\!+}(n)\). This condition is equivalent to the requirement that the acoustic tensor \(Q(F,\eta )\in \operatorname{Sym}(n)\) with \(Q_{ik}(F,\eta )=\sum _{j,l=1}^{n} \frac{\partial ^{2}W(F)}{\partial F_{ij}\partial F_{kl}}\cdot \eta _{j} \eta _{l}\) is positive semi-definite for all directions \(\eta \in \mathbb{R}^{n}\), where
For the dynamic problem, a non-negative acoustic tensor means that the system is hyperbolic [19, 44]. When the dynamic equation is linearized at \(F\in \operatorname{GL}^{\!+}(n)\), then there exists a traveling wave solution with real wave speeds if and only if the problem is Legendre-Hadamard elliptic at \(F\) [67]. Moreover, the static response is metastable (stable against infinitesimal perturbations) under Legendre-Hadamard ellipticity (if \(c>0\) in (1.2)). The loss of ellipticity is generally related to instability phenomena (separation into arbitrary fine phase mixtures [26, 67], shear banding) and possible discontinuous equilibrium solutions [59].
Checking rank-one convexity for a given nonlinear elastic material can be quite challenging, see e.g., [8, 35, 47, 56] and Appendix D, although John Ball’s polyconvexity [6] as an easy-to-verify sufficient condition can often be helpful [36, 62]. A certain simplification occurs in the isotropic case. Indeed, any isotropic energy on \(\operatorname{GL}^{\!+}(n)\) admits a representation in terms of the singular values \(W(F)=g(\lambda _{1},\ldots ,\lambda _{n})\), where \(g\colon (0,\infty )^{n}\to \mathbb{R}\) is permutation invariant. In planar isotropic hyperelasticity, Knowles and Sternberg have provided a criterion for rank-one convexity in terms of \(g\), conclusively reducing the problem to the singular values representation [14, 31,32,33, 69], see also [11, 15, 55, 71, 73, 75]. In the Knowles-Sternberg result, a family of inequality constraints in terms of first and second derivatives of \(g\) (including the Baker-Ericksen inequality [5]) has to be checked, which can still be daunting in practice.
The ellipticity condition in the planar and isotropic case has also been reformulated in terms of yet different representations, see, e.g., [15, 27, 60], always in the form of a set of differential inequality constraints involving the used special representation. Generalizations to the case of functions defined not on \(\operatorname{GL}^{\!+}(2)\) but on \(\mathbb{R}^{2\times 2}\) have been obtained by Aubert [3] and Hamburger [27]. For some special families of energy functions more detailed information is available. For example, in the fluid-like case [12]
Moreover, for the Hadamard-material [7, 12, Theorem 5.58ii)] (see also [13])
In a recent contribution [34, 38], we have been able to classify all planar, isotropic rank-one convex functions \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) which are isochoric (conformally invariant), i.e., satisfy
For these energies we have the simple characterizationFootnote 1
where \(\lambda _{1},\lambda _{2}>0\) are the singular values of \(F\). Similarly, rank-one convexity in isotropic planar incompressible elasticity \(W\colon \operatorname{SL}(2)\to \mathbb{R}\) can be easily checked [22]: for an energy of the form
These results also allow for an explicit calculation of the quasiconvex relaxation for conformally invariant and incompressible isotropic planar hyperelasticity [37, 38].
1.1 The Volumetric-Isochoric Split
In isotropic linear elasticity, the quadratic elastic energy \(W^{\mathrm{lin}}\) and the linear Cauchy stress tensor \(\sigma ^{\mathrm{lin}}\) can be uniquely represented as

where \(\mu ,\lambda \) are the Lamé-constants, \(\kappa \) is the bulk-modulus, \(\nabla u\) denotes the displacement gradient and  is the deviatoric part of \(X\in \mathbb{R}^{n\times n}\), cf. Appendix A. The right hand side of the energy is automatically additively separated into pure infinitesimal shape change and infinitesimal volume change, respectively, with a similar additive split of the Cauchy stress tensor into a deviatoric part and a spherical part, depending only on the shape change and volumetric change, respectively.
is the deviatoric part of \(X\in \mathbb{R}^{n\times n}\), cf. Appendix A. The right hand side of the energy is automatically additively separated into pure infinitesimal shape change and infinitesimal volume change, respectively, with a similar additive split of the Cauchy stress tensor into a deviatoric part and a spherical part, depending only on the shape change and volumetric change, respectively.
A natural finite strain extension of (1.9) is given by the additive volumetric-isochoric split [30], i.e., by assuming the energy potential \(W\) to have the form
where \(W_{\mathrm{iso}}\) is isochoric (conformally invariant), since \(W_{\mathrm{iso}}(s \hspace{0.03em} F)=W_{\mathrm{iso}}\big ( \frac{s\hspace{0.03em}F}{\sqrt[n]{\det (s\hspace{0.03em}F)}}\big )= W_{ \mathrm{iso}}\big (\frac{F}{\sqrt[n]{\det F}}\big )\) for all \(s>0\). Here, again, the energy contribution is additively split into the isochoric part taking only the shape change into account (depending only on \(\frac{F}{\sqrt[n]{\det F}}\)), and a part penalizing only the volumetric extension in \(\det F\). Note the multiplicative decomposition

of the deformation gradient \(F\) itself into volume preserving and shape changing part [17, 18, 23, 43, 54, 57, 66, 72]. Such type of energy functions are often used when modeling slightly compressible material behavior [9, 10, 16, 28, 54] or when otherwise no detailed information on the actual response of the material is available [19, 45, 72]. In the nonlinear regime, this split is not a fundamental law of nature for isotropic bodies (as in the linear case) but rather introduces a convenient form of the energy. Formally, this split can also be generalized to the anisotropic case, where it shows, however, some severe deficiencies [17, 43] from a modeling point of view.Footnote 2
It has been first shown by Richter [23, 53, 57, 58] (see also Flory [18] and Sansour [61]) that the accompanying symmetric nonlinear Kirchhoff stress tensor \(\tau =\det F\cdot \sigma \) (but not the Cauchy stress as repeatedly claimed in [44, 45]) admits a similar additive structure in the sense that

in which the deviatoric part of the Kirchhoff stress only depends on \(W_{\mathrm{iso}}\) and the spherical part only depends on \(W_{\mathrm{vol}}\). A typical example of the foregoing volumetric-isochoric format is the geometrically nonlinear quadratic Hencky energy [29, 36, 52, 65]

as well as its physically nonlinear extension, the exponentiated Hencky-model [48, 50]

which has been used for the stable computation of the inversion of tubes [46], the modeling of tire-derived material [42] or applications in bio-mechanics [63]. While it is well known that (1.13) and (1.14) are overall not rank-one convex [50], there does not exist any elastic energy of the type \(W(F)=\mathcal{W}(\lVert \operatorname{dev}_{n}\log V \rVert ^{2})\) with \(\mathcal{W}\colon \mathbb{R}_{+}\to \mathbb{R}\), \(n\geq 3\) that is rank-one convex [20]. The situation is surprisingly completely different for the planar case. Indeed, (1.14) for \(n=2\) is not only rank-one convex, but also polyconvex [21, 51] if \(k\geq \frac{1}{8}\).
Because of this counter-intuitive result when descending from three-dimensions to two-dimensions, we became interested in the precise qualitative nature of the volumetric-isochoric split in the planar case with respect to rank-one convexity.Footnote 3 In the planar isotropic case (exclusively), the isochoric energy part \(W_{\mathrm{iso}}\) admits a number of equivalent representations, e.g.,
In particular, for planar additively volumetric-isochoric split energies we can be uniquely written without loss of generality [34, Lemma 3.1]
where \(\lambda _{1},\lambda _{2}>0\) denote the singular values of \(F\) and \(h,f\) are given functions. It is now tempting to believe that the rank-one convexity conditions on \(\widehat{\psi }\) and \({\widehat{f}}\), respectively on \(W_{\mathrm{iso}}\) and \(W_{\mathrm{vol}}\) also allow for a sort of split (like for the Kirchhoff stress tensor in (1.12)) and can be reduced to separate statements on \(h\) and \(f\). However, this is not even the case in planar linear elasticity, where \(W^{\mathrm{lin}}\) from (1.9) is rank-one convex in the displacement gradient \(\nabla u\) if and only if \(\mu \geq 0\) and \(\mu +\kappa \geq 0\), see Appendix A. This means that rank-one convexity of \(W^{\mathrm{lin}}\) implies that \(W_{\mathrm{iso}}^{\mathrm{lin}}\) is rank-one convex, whereas \(W_{\mathrm{vol}}^{\mathrm{lin}}\) might not be rank-one convex. We therefore need to expect some coupling in the conditions for \(h\) and \(f\).
Our main result in this respect (Theorem 2.6) can be summarized as follows: If \(W\) is altogether rank-one convex then, either \(W_{\mathrm{iso}}\) or \(W_{\mathrm{vol}}\) must be rank-one convex (i.e., \(h\) or \(f\) are convex), but contrary to isotropic linear elasticity, \(W_{\mathrm{iso}}\) may also be non rank-one convex (see the example in Sect. 2.8). Although the conditions for \(h\) and \(f\) do not decouple completely, it is possible to reduce rank-one convexity to a family of coupled one-dimensional conditions.
The paper is now structured as follows. After a short introduction and visualization of rank-one convexity on \(\operatorname{GL}^{\!+}(2)\), we start with criteria by Knowles and Sternberg for the arbitrary objective-isotropic case on the two-dimensional set of the singular values \(\lambda _{1},\lambda _{2}>0\) of \(F\). Lemma 2.4 gives the corresponding conditions for the volumetric-isochoric split. The main Theorem 2.6 shows that it is indeed possible to reduce the conditions to a coupled family of one-dimensional differential inequalities which makes testing for rank-one convexity much more convenient in the volumetric-isochoric split case. Apart from a list of additional necessary conditions, we derive a simple classification for generalized Hadamard energies and give two examples of non-trivial rank-one convex energies for which \(W_{\mathrm{iso}}\) and \(W_{\mathrm{vol}}\), respectively, are not rank-one convex. Finally, we show how criteria for the invertibility of the Cauchy stress response are also simplified in the volumetric-isochoric split case and highlight the connection of this invertibility property to rank-one convexity.
2 Rank-One Convexity Conditions on \(\operatorname{GL}^{\!+}(2)\)
We first recall the following basic definitions.
Definition 2.1
An energy function \(W\colon \mathbb{R}^{n\times n}\to \mathbb{R}\) is called rank-one convex if the mapping
Definition 2.2
An energy function \(W\in C^{2}(\mathbb{R}^{n\times n};\mathbb{R})\) is called Legendre-Hadamard elliptic if
which is equivalent to rank-one convexity.
Throughout the following, we will use the identification \(W(F)=g(\lambda _{1},\lambda _{2})\) for any isotropic planar energy function \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\), where \(\lambda _{1},\lambda _{2}>0\) are the singular values of \(F\), i.e., the eigenvalues of \(\sqrt{F^{T}F}\), and the function \(g\colon (0,\infty )^{2}\to \mathbb{R}\) is permutation invariant.
2.1 Ellipticity Domains for Some Nonlinear Energy Functions
For an isotropic energy function \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\), it is possible to visualize the ellipticity domain in terms of the singular values \(\lambda _{1},\lambda _{2}>0\) of \(F\), as shown in Fig. 1. The isotropy of \(W\) ensures the symmetry about the bisector, i.e., \(W(\lambda _{1}, \lambda _{2})=W(\lambda _{2},\lambda _{1})\). For purely isochoric energies \(W(F)=W_{\mathrm{iso}}\big (\frac{F}{\sqrt{\det F}}\big )=h\big ( \frac{\lambda _{1}}{\lambda _{2}}\big )\), the ellipticity domain consists only of cones and can therefore be reduced to a one-dimensional problem at \(\det F=1\) or any other fixed determinant. Of course, this is not the case for energies with an arbitrary volumetric part \(f(\lambda _{1} \lambda _{2})\).
The ellipticity domain in terms of the singular values \(\lambda _{1},\lambda _{2}>0\) of the exponentiated Hencky-model with \(k<\frac{1}{8}\). Left: Only the non rank-one convex isochoric part \(h(t)=e^{\frac{1}{10} \hspace{0.07em} (\log t)^{2}}\). Rank-one convexity at one point on the curve \(\det F=\lambda _{1}\lambda _{2}=c\) (black) for arbitrary \(c>0\) implies rank-one convexity at the straight line (green) connecting the origin to this point. Right: For additive coupling with the volumetric part \(f(z)=\frac{1}{1000}\left (z-\frac{1}{z}\right )^{2}\), the above invariance is lost for non-isochoric energies
2.2 The Classical Knowles and Sternberg Ellipticity Criterion
For rank-one convexity on \(\operatorname{GL}^{\!+}(2)\), Knowles and Sternberg [32, 33] (see also [67, p. 308]) established the following important and useful criterion.
Lemma 2.3
(Knowles and Sternberg [32, 33], cf. [3, 4, 11, 55, 67, 68, 70])
Let \(W\colon \operatorname{GL}^{\!+}(2) \to \mathbb{R}\) be an objective-isotropic function of class \(C^{2}\) with the representation in terms of the singular values of the deformation gradient \(F\) given by \(W(F)=g(\lambda _{1},\lambda _{2})\), where \(g\in C^{2}((0,\infty )^{2},\mathbb{R})\). Then \(W\) is rank-one convex if and only if the following five conditions are satisfied:
-
i)
\(\displaystyle \underbrace{g_{xx}\geq 0\quad \textit{and}\quad g_{yy}\geq 0}_{ \textit{``TE-inequalities'' (separate convexity)}} \quad \textit{for all}\ x,y\in (0,\infty )\),
-
ii)
\(\displaystyle \underbrace{\frac{x\hspace{0.07em}g_{x}-y\hspace{0.07em}g_{y}}{x-y}\geq 0}_{ \textit{``BE-inequalities''}}\quad \textit{for all}\ x,y\in (0,\infty )\,,\; x\neq y\),
-
iii)
\(\displaystyle g_{xx}-g_{xy}+\frac{g_{x}}{x}\geq 0\ \textit{and}\ g_{yy}-g_{xy}+\frac{g_{y}}{y}\geq 0\quad \textit{for all}\ x,y \in (0,\infty )\,,\; x=y\),
-
iv)
\(\displaystyle \sqrt{g_{xx}\,g_{yy}}+g_{xy}+\frac{g_{x}-g_{y}}{x-y} \geq 0\quad \textit{for all}\ x,y\in (0,\infty )\,,\; x\neq y\),
-
v)
\(\displaystyle \sqrt{g_{xx}\,g_{yy}}-g_{xy}+\frac{g_{x}+g_{y}}{x+y} \geq 0\quad \textit{for all}\ x,y\in (0,\infty )\).
Furthermore, if all the above inequalities are strict, then \(W\) is strictly rank-one convex.
This criterion has recently been generalized to plane strain orthotropic materials [1], see also [39, 74]. Hamburger [27] gives an extension to \(\mathbb{R}^{2\times 2}\) instead of \(\operatorname{GL}^{\!+}(2)\) in the same format. In this paper, we restrict ourselves to the class of two-dimensional isotropic energy functions \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) with additive volumetric-isochoric split
as introduced in (1.15), where \(\lambda _{1},\lambda _{2}\in (0,\infty )\) are the singular values of \(F\) and \(h\colon (0,\infty )\to \mathbb{R}\) satisfies \(h(t)=h\big (\frac{1}{t}\big )\) for all \(t\in (0,\infty )\).Footnote 4 Note that the case \(W(F)=+\infty \) is excluded by definition.
Starting with a rank-one convex energy function \(W\) with additive volumetric-isochoric split, it is not clear whether the separate parts \(W_{\mathrm{iso}}\) and \(W_{\mathrm{vol}}\) need to be rank-one convex, too. Indeed, subsequently we will see that this is not always the case.
2.3 Necessary and Sufficient Conditions for the Planar Volumetric-Isochoric Split
The following Lemma expresses the Knowles-Sternberg criterion (Lemma 2.3) in terms of the functions \(h\) and \(f\) for the specific form \(g(x,y)=h\big (\frac{x}{y}\big )+f(x \hspace{0.03em} y)\) of \(g\) in the case of an additive volumetric-isochoric split.
Lemma 2.4
Let \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) be an objective-isotropic function of class \(C^{2}\) with additive volumetric-isochoric split, with the representation in terms of the singular values of the deformation gradient \(F\) given by \(W(F)=g(\lambda _{1},\lambda _{2})=h\big ( \frac{\lambda _{1}}{\lambda _{2}}\big )+f(\lambda _{1}\lambda _{2})\), where \(f,h\in C^{2}((0,\infty ),\mathbb{R})\) andFootnote 5\(h(t)=h\big (\frac{1}{t}\big )\) for all \(t\in (0,\infty )\). Then \(W\) is rank-one convex if and only if the following four conditions are satisfied:
-
A)
\(\displaystyle t^{2} \hspace{0.07em} h''(t)+z^{2} \hspace{0.07em} f''(z)\geq 0\quad \textit{for all}\ t,z\in (0,\infty )\) (equivalent to Knowles and Sternberg i)),
-
B)
\(\displaystyle h'(t)\geq 0\quad \textit{for all}\ t\geq 1\) (equivalent to Knowles and Sternberg ii)),
-
C)
\(\displaystyle \frac{2t}{t-1} \hspace{0.07em} h'(t)-t^{2} \hspace{0.07em} h''(t)+z^{2} \hspace{0.07em} f''(z)\geq 0 \ \textit{or}\ a(t)+\left [b(t)-c(t)\right ]z^{2} \hspace{0.07em} f''(z)\geq 0\quad \textit{for all}\ t,z\in (0,\infty )\,,\;t\neq 1\) (equivalent to Knowles and Sternberg iv)),
-
D)
\(\displaystyle \frac{2t}{t+1} \hspace{0.07em} h'(t)+t^{2} \hspace{0.07em} h''(t)-z^{2} \hspace{0.07em} f''(z)\geq 0 \ \textit{or}\ a(t)+\left [b(t)+c(t)\right ]z^{2} \hspace{0.07em} f''(z)\geq 0\quad \textit{for all}\ t,z\in (0,\infty )\) (equivalent to Knowles and Sternberg v)),
where
Remark 2.5
Note that Knowles and Sternberg condition iii) is redundant in this case, since it is already implied by condition B), cf. [11].
Proof
We start by computing the partial derivatives
of the energy function with respect to the singular values. Next, we utilize the specific form of the additive split by introducing the transformation of variables

which allows us to decouple the conditions for \(g(x,y)\) into conditions for \(f(z)\) and \(h(t)\). Moreover, the invariance property \(h(t)=h\big (\frac{1}{t}\big )\) of the isochoric part \(h\) yields
Note that for \(t=1\), equation (2.7) already impliesFootnote 6
In the following, we transform the conditions i)-v) of Knowles and Sternberg Lemma 2.3 one by one.
Knowles and Sternberg i) \(g_{xx}\geq 0\) and \(g_{yy}\geq 0\) for all \(x,y,\in (0,\infty )\): We compute
The first condition (2.8) already has the desired form. For the second condition (2.9) we use the symmetry property (2.7) for a further transformation, using the equality
to substitute

which is equivalent to condition (2.8). Thus

Note that A) implies \(\displaystyle \inf _{t\in (0,\infty )}t^{2} \hspace{0.07em} h''(t)\,,\;\inf _{z\in (0,\infty )}z^{2} \hspace{0.07em} f''(z)\in \mathbb{R}\).
Knowles and Sternberg ii) \(\displaystyle \frac{x\hspace{0.07em}g_{x}-y\hspace{0.07em}g_{y}}{x-y}\geq 0\) for all \(x,y\in (0,\infty )\,,\; x\neq y\): We compute
Since the invariance property (2.7), i.e., \(h(t)=h \big (\frac{1}{t}\big )\) for all \(t\in \mathbb{R}\), yields
we obtain the equivalence

Note that B) implies \(h'(1)=0\) as well as \(h''(1)\geq 0\).
Knowles and Sternberg iii) \(\displaystyle g_{xx}-g_{xy}+\frac{g_{x}}{x}\geq 0\,, \; g_{yy}-g_{xy}+ \frac{g_{y}}{y}\geq 0\quad \forall \; x=y\in (0,\infty )\):
We compute
Thus

the latter condition being already implied by condition B), which in turn follows from Knowles and Sternberg ii).
Knowles and Sternberg iv)+v) We compute
and substitute
to find
For further computations, we need to express the Knowles-Sternberg conditions in a form not involving square rootsFootnote 7 in the term \(\sqrt{g_{xx}\,g_{yy}}\). However, we will need to pay close attention to the sign of occurring terms.
Knowles and Sternberg iv) \(\displaystyle \sqrt{g_{xx}\,g_{yy}}+g_{xy}+\frac{g_{x}-g_{y}}{x-y} \geq 0\) for all \(x,y\in (0,\infty )\,,\; x\neq y\): It holds
For the first case in equation (2.23) we compute
For the second case in equation (2.23) we start with
and compute

Thus, with the definitions
we obtain the equivalence

Knowles and Sternberg v) \(\displaystyle \sqrt{g_{xx}\,g_{yy}}-g_{xy}+\frac{g_{x}+g_{y}}{x+y} \geq 0\) for all \(x,y\in (0,\infty )\): It holds
For the first case in equation (2.27) we compute
For the second case in equation (2.27) we start with
and compute

Thus with the previous definitions
we find

thereby establishing the last equivalence and completing the proof of Lemma 2.4. □
2.4 Reduction to a Family of Coupled One-Dimensional Differential Inequalities
In the following theorem we show that, surprisingly, it is possible to reduce the two-dimensional problem of rank-one convexity for planar objective-isotropic energies with additive volumetric-isochoric split to only coupled one-dimensional conditions.
Theorem 2.6
Let \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) be an objective-isotropic function of class \(C^{2}\) with additive volumetric-isochoric split with the representation in terms of the singular values of the deformation gradient \(F\) via \(W(F)=g(\lambda _{1},\lambda _{2})=h\big ( \frac{\lambda _{1}}{\lambda _{2}}\big )+f(\lambda _{1}\lambda _{2})\), where \(f,h\in C^{2}((0,\infty ),\mathbb{R})\), and let \(h_{0}=\inf _{t\in (0,\infty )}t^{2} \hspace{0.07em} h''(t)\) and \(f_{0}=\inf _{z\in (0,\infty )}z^{2} \hspace{0.07em} f''(z)\). Then \(W\) is rank-one convex if and only if
-
1)
\(\displaystyle h_{0}+f_{0}\geq 0\),
-
2)
\(\displaystyle h'(t)\geq 0\quad \textit{for all}\ t\geq 1\),
-
3)
\(\displaystyle \frac{2t}{t-1} \hspace{0.07em} h'(t)-t^{2} \hspace{0.07em} h''(t)+f_{0}\geq 0\) or \(\displaystyle a(t)+\left [b(t)-c(t)\right ]f_{0}\geq 0\quad \textit{for all}\ t\in (0,\infty )\,,\;t\neq 1\),
-
4)
\(\displaystyle \frac{2t}{t+1} \hspace{0.07em} h'(t)+t^{2} \hspace{0.07em} h''(t)-f_{0}\geq 0 \ \textit{or}\ a(t)+\left [b(t)+c(t)\right ]f_{0} \geq 0\quad \textit{for all}\ t\in (0,\infty )\),
where
Proof
First, let the conditions 1)–4) be satisfied for some energy \(W\). Choose a function \({\widehat{f}}\colon (0,\infty )\to \mathbb{R}\) such that \(z^{2} \hspace{0.07em} {\widehat{f}}''(z)\equiv f_{0}\) and let  . Then conditions 1)–4) for the original energy \(W\) are equivalent to conditions A)–D) in Lemma 2.4 for the energy \({\widehat{W}}\). Therefore, \({\widehat{W}}\) is rank-one convex. For
. Then conditions 1)–4) for the original energy \(W\) are equivalent to conditions A)–D) in Lemma 2.4 for the energy \({\widehat{W}}\). Therefore, \({\widehat{W}}\) is rank-one convex. For  , we also find
, we also find
thus \({\widetilde{f}}\) is convex. Finally, \(W\) can be decomposed into the sum
of the rank-one convex energy \({\widehat{W}}\) and the \(F\mapsto {\widetilde{f}}(\det F)\), which is rank-one convex due to the convexity of \({\widetilde{f}}\). Therefore, the energy \(W\) is rank-one convex.
Now, let \(W\) be rank-one convex. We observe that for given \(h\) and arbitrary fixed \(t>0\), each of the conditions A)–D) of Lemma 2.4 can be written as an inequality \(P_{t,h}(z^{2}f''(z))\geq 0\) for some continuous function \(P_{t,h}\). Furthermore, using the same functions, each of the conditions 1)–4) can be expressed in the form \(P_{t,h}(f_{0})\geq 0\). If \(W\) is rank-one convex, i.e., if the conditions A)–D) are satisfied for all \(z\in (0,\infty )\), then
due to continuity, therefore conditions 1)–4) hold as well. □
Corollary 2.7
Rank-one convexity of the energy \(W(F)=h\bigl (\frac{\lambda _{1}}{\lambda _{1}}\bigr )+f(\lambda _{1} \hspace{0.07em} \lambda _{2})\) implies
for all \(t\in (0,\infty )\).
Proof
For arbitrary \(\eta >0\), consider the rank-one convex class of energy functions

such that the convex volumetric part \({\widehat{f}}_{\eta }\colon (0,\infty )\to \mathbb{R}\) satisfies \(z^{2} \hspace{0.07em} {\widehat{f}}_{\eta }''(z)\equiv \eta \). Then
If \(b(t_{0})+c(t_{0})<0\) for some arbitrary \(t_{0}\in (0,\infty )\), then condition 4) of Theorem 2.6 for the energy \(W_{\eta }(F)\), which reads
cannot be satisfied for \(\eta \to \infty \), in contradiction to the rank-one convexity of the energy function \(W_{\eta }(F)\) for all \(\eta >0\). Thus \(b(t)+c(t)\geq 0\) for all \(t\in (0,\infty )\). □
2.5 Further Necessary Conditions for Rank-One Convexity
We continue the discussion with a list of necessary conditions for rank-one convexity of an energy with volumetric-isochoric split in terms of the isochoric part \(h\) and volumetric part \(f\).
Lemma 2.8
Consider an arbitrary isotropic rank-one convex energy function \(W\colon \operatorname{GL}^{\!+}(2) \to \mathbb{R}\) with additive volumetric-isochoric split \(W(F)=h\bigl (\frac{\lambda _{1}}{\lambda _{2}}\bigr )+f(\lambda _{1} \lambda _{2})\). Then
-
a)
\(h\) is globally convex or \(f\) is globally convex.
-
b)
the mapping \(x\mapsto h(x)+f(x)\) is globally convex on \((0,\infty )\).
-
c)
\(h'(t)\geq 0\) for all \(t>1\) and \(h'(t)\leq 0\) for all \(t<1\), i.e., \(h\) is monotone increasing on \([1,\infty )\) and monotone decreasing on \((0,1]\).
-
d)
\(t \hspace{0.07em} h''(t)+h'(t)\geq 0\) for all \(t>0\). The inequality is strict if the energy is strictly rank-one convex.
-
e)
\(\left (t+3\right )h'(t)+2t \hspace{0.07em} (t+1) \hspace{0.07em} h''(t)\geq 0\) for all \(t>0\).
Proof
Condition a) The separate convexity condition 1) in Theorem 2.6 states
Condition b) For any \(a>0\), rank-one convexity of \(W\) implies the convexity of \(W\) along the straight line \(t\mapsto \operatorname{diag}(a,1)+t\operatorname{diag}(1,0)\) in rank-one direction \(\operatorname{diag}(1,0)\), i.e., the convexity of the mapping
and thus the convexity of the mapping \(x\mapsto h(x)+f(x)\).
Condition c) The monotonicity condition is already known as condition 2) in Theorem 2.6 (as well as Lemma 2.4).
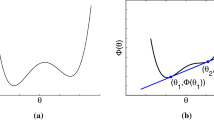
Condition d) The inequality can be obtained by considering the restriction \(W_{\mathrm{SL}}=W|_{\operatorname{SL}(2)}\) of \(W\) to the special linear group \(\{F\in \operatorname{GL}^{\!+}(2) \,|\,\det F = 1\}\). Then rank-one convexity of \(W\) implies rank-one convexity [37] of \(W_{\mathrm{SL}}\) with respect to \(\operatorname{SL}(2)\). Recall that any function \(W_{\mathrm{SL}}\colon \operatorname{SL}(2)\to \mathbb{R}\) can be expressed in the form (1.8), i.e.,
with \(\phi \colon [0,\infty )\to \mathbb{R}\), and \(W_{\mathrm{SL}}\) is rank-one convex on \(\operatorname{SL}(2)\) if and only if \(\phi \) is monotone and convex [37]. For \(W_{\mathrm{SL}}=W|_{\operatorname{SL}(2)}\), we find
for all \(F\in \operatorname{SL}(2)\) with singular values \(\lambda _{\mathrm{max}}>\lambda _{\mathrm{min}}\) and thus
Then for any \(t\geq 1\),
and thus
due to the rank-one convexity of \(W_{\mathrm{SL}}\). For \(t\leq 1\), the inequality can be obtained analogously. If the energy is strictly rank-one convex, it holds \(\phi ''(x)>0\) for all \(x>0\) and thus \(t \hspace{0.07em} h''(t)+h'(t)>0\) for all \(t>0\).
Condition e) The inequality follows directly from Lemma 2.7 where it is shown that rank-one convexity implies
□
2.6 Application to Generalized Hadamard Energies
In particular, our rank-one characterization applies to the family of planar isotropic functions

Here, \(\mathbb{K}\geq 1\) is the so-called distortion function, which plays an important role in the theory of quasiconformal mappings [2, 38]. Note that \(\mathbb{K}\equiv 1\) if and only if \(\varphi \) is conformal. It is well known that the mapping \(F\mapsto \mathbb{K}(F)\) itself is rank-one convex and even polyconvex on \(\operatorname{GL}^{\!+}(2)\). Using our characterization for rank-one convexity of volumetric-isochoric split energies, we obtain the following lemma.
Lemma 2.9
The energy function \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) with \(W(F)=\mu \,\mathbb{K}(F)+f(\det F)\) is rank-one convex if and only if \(f\) is convex.
Proof
We first observe that
and calculate the derivatives \(h'(t)=\frac{1}{2}\left (1-\frac{1}{t^{2}}\right )\) and \(h''(t)=\frac{1}{t^{3}}\,\). Thus \(h\) is globally convex and (strictly) increasing for \(t>1\), hence the isochoric term \(\mu \hspace{0.07em} \mathbb{K}\) is rank-one convex. If the volumetric term \(f\) is convex as well, the energy function \(W\) is rank-one convex as a sum of two rank-one convex functions.
Now, in order to show the reverse implication, let \(W\) be rank-one convex. Then \(W\) is separately convex, which is expressed by condition 1) of Theorem 2.6 as \(h_{0}+f_{0}\geq 0\). We compute
and thus
Therefore, the function \(f\) must be convex (which implies that the volumetric part \(F\mapsto f(\det F)\) is rank-one convex). □
The result of Lemma (2.9) should be compared with the particular planar and quadratic case [7, 12, 26, Theorem 5.58ii)] \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) of the Hadamard-material, for which
In an intriguing recent contribution [24, 25], the quasiconvex envelope for the Hadamard material has been computed analytically for a non-convex function \(f\) and sufficiently large shear modulus \(\mu \). It would be interesting to obtain a similar relaxation result for \(W(F)=\frac{\mu }{2} \hspace{0.07em} \frac{\lVert F \rVert ^{2}}{\det F}+f(\det F)\).
2.7 Idealized Planar Isotropic Nonlinear Energy Function
From a modeling perspective, it is a useful idealization to assume that the isochoric and volumetric response are governed by the same functional form. Consider an energy function \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) of the form
where \(h\in C^{2}((0,\infty );\mathbb{R})\) with \(h(t)=h\bigl (\frac{1}{t}\bigr )\) for all \(t\in (0,\infty )\) and \(\mu ,\kappa >0\). This class of energies includes, for example, the Hencky energy (1.13) and the exponentiated Hencky energy (1.14). Note that any energy \(W\) of this form is tension-compression symmetric, i.e., satisfies \(W(F)=W(F^{-1})\) for all \(F\in \operatorname{GL}^{\!+}(2)\).
Theorem 2.6 immediately shows that an energy of the form (2.43) is rank-one convex if and only if \(h\) is convex. In this case, the volumetric and isochoric parts are rank-one convex, individually. Thus for this particular type of split energy function, rank-one convexity is indeed equivalent to rank-one convexity of both the volumetric and the isochoric part. Moreover, according to the results of Sect. 3, the corresponding Cauchy stress-stretch response is locally invertible if \(h\) is uniformly convex.
2.8 Examples of Non-trivial Rank-One Convex Energies
In contrast to the class (2.41) of functions, it is possible to find rank-one convex energies with either a non rank-one convex volumetric part \(W_{\mathrm{vol}}\) or non rank-one convex isochoric part \(W_{\mathrm{iso}}\). As an example, consider the energy
The isochoric part \(W_{\mathrm{iso}}=e^{\frac{1}{10}\left (\log \frac{\lambda _{1}}{\lambda _{2}}\right )^{2}}\) is not rank-one convex, cf. Fig. 1. However, with formula (C.5) the infinitesimal shear modulusFootnote 8\(\mu =\psi '(1)=\frac{1}{5}>0\) and the infinitesimal bulk modulus \(\kappa =f''(1)=\frac{2}{15}>0\) imply rank-one convexity in the infinitesimal case. Similar to the non rank-one convex energy in Fig. 1, numerical results for the Knowles-Sternberg criterion directly suggest that the energy (2.44) is everywhere rank-one convex on \(\operatorname{GL}^{\!+}(2)\). In order to prove rank-one convexity with Theorem 2.6, we compute
and determine the constant \(f_{0}\):

Furthermore, numerical calculations yield  , thus \(h_{0}+f_{0}>0\). In addition, we compute
, thus \(h_{0}+f_{0}>0\). In addition, we compute
The remaining conditions 3) and 4) of Theorem 2.6 are too complex to be solved analytically, but are numerically visualized in Fig. 2.
Visualization of the rank-one convexity conditions 3) and 4) of Theorem 2.6. Note that for each condition and each \(t\in (0,\infty )\), only one of the two terms must be positive, which is the case here
As a second example, consider the energy
with a non rank-one convex volumetric part \(W_{\mathrm{vol}}\) in the form of a double-well potential. Again, with formula (C.5) the infinitesimal shear modulusFootnote 9\(\mu =\psi '(1)=\frac{48}{5}>0\) and the infinitesimal bulk modulus \(\kappa =f''(1)=-8<0\) imply rank-one convexity in the infinitesimal case. Similar to the non rank-one convex energy in Fig. 1, employing numerical calculations for the Knowles-Sternberg criterion directly suggests that the energy (2.47) is everywhere rank-one convex on \(\operatorname{GL}^{\!+}(2)\). Again, the rank-one convexity of \(W\) can be shown using Theorem 2.6. First, we compute
For \(z=1\), we obtain the infimum  , whereas
, whereas  can be calculated similarly to the value of \(f_{0}\) in Example (2.44). Thus \(h_{0}+f_{0}>0\). In addition, we compute
can be calculated similarly to the value of \(f_{0}\) in Example (2.44). Thus \(h_{0}+f_{0}>0\). In addition, we compute
Again, the remaining conditions 3) and 4) of Theorem 2.6 are too complex to allow for analytical solutions, but are easily verified numerically similar to the case shown in Fig. 2.
3 Invertibility of the Cauchy Stress Tensor in Planar Elasticity
The volumetric-isochoric split allows for a simplified investigation of invertibility for the Cauchy stress-stretch law [64] as well. First, recall that in planar linear isotropic elasticity, the energy potential and the Cauchy stress response are given by

respectively. Then [40, 41, 49]
Lemma 3.1
Assume that \(W^{\mathrm{lin}}\) is strictly rank-one convex and \(\kappa >0\). Then \(\mu >0\) (cf. Appendix A), \(\kappa >0\), and the Cauchy stress-strain law is uniquely invertible.
Now, consider the planar nonlinear isotropic case with an additive volumetric-isochoric split.
Lemma 3.2
Assume that \(W(F)=W_{\mathrm{iso}}\big (\frac{F}{\sqrt{\det F}}\big )+W_{ \mathrm{vol}}(\det F)\) is strictly rank-one convex and \(f\) is uniformly convex with \(W_{\mathrm{vol}}(F)=f(\det F)\). Then the Cauchy stress-stretch law is locally invertible.
Proof
Again, we use the notation \(W(F)=g(\lambda _{1},\lambda _{2})=h\big ( \frac{\lambda _{1}}{\lambda _{2}}\big )+f(\lambda _{1}\lambda _{2})\) and compute principle Cauchy stresses
Thus \(\widehat{\sigma }\) has the form

with \(a,b\in \mathbb{R}\). We compute
where
Thus
The stress-strain response is locally invertible if
with \(t=\frac{\lambda _{1}}{\lambda _{2}}\) and \(z=\lambda _{1}\lambda _{2}\), with inequality (3.8) being satisfied due to the implications

□
Corollary 3.3
Let \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) with \(W(F)=h\bigl (\frac{\lambda _{1}}{\lambda _{2}}\bigr )+f(\det (F))\) for all \(F\in \operatorname{GL}^{\!+}(2)\) with singular values \(\lambda _{1},\lambda _{2}\). If \(f''(z)>0\) for all \(z\in (0,\infty )\) and \(t \hspace{0.07em} h''(t)+h'(t)>0\) for all \(t\in (0,\infty )\), then the Cauchy stress-stretch law is locally invertible.
Corollary 3.4
Let \(W\colon \operatorname{GL}^{\!+}(2)\to \mathbb{R}\) with \(W(F)=h\bigl (\frac{\lambda _{1}}{\lambda _{2}}\bigr )+f(\det F)\) for all \(F\in \operatorname{GL}^{\!+}(2)\) with singular values \(\lambda _{1},\lambda _{2}\) for uniformly convex functions \(h,f\colon (0,\infty )\to \mathbb{R}\). Then the Cauchy stress-stretch law is locally invertible.Footnote 10
4 Conclusion
Our investigation clearly demonstrates that for planar isotropic hyperelasticity, assuming a volumetric-isochoric split of the elastic energy endows the theory with a lot of additional mathematical structure which can be consequently exploited. Indeed, we have shown how the classical Knowles-Sternberg planar ellipticity criterion - which is represented by a family of two-dimensional differential inequalities - can be reduced to a family of only one-dimensional coupled differential inequalities for split energies, which allows for a much more accessible rank-one convexity criterion.
By using these reduced inequalities, we could show that it is possible for a volumetric-isochorically split energy to be altogether rank-one convex even if the isochoric part is non-elliptic, in stark contrast to the linear case, where only the volumetric part of a rank-one convex energy might be non-elliptic. We also applied our method to the general class of Hadamard-type materials and obtained a universal classification of their rank-one convexity.
In future contributions, based on encouraging preliminary results, we aim to extend our investigation from rank-one convexity to polyconvexity. Unfortunately, our methods are at present strictly restricted to the planar isotropic case; it remains to be seen whether similar statements can be established for the three-dimensional case as well.
Notes
The isotropy of the energy implies \(h(t)=h\big (\frac{1}{t}\big )\) for all \(t\in (0,\infty )\), cf. equation (1.15).
For example, a perfect sphere made of an anisotropic material and subject only to all around pressure would remain spherical for volumetric-isochorically decoupled energies.
The three-dimensional case of volumetric-isochoric split energies on \(\operatorname{GL}^{\!+}(3)\) has previously been considered in [44], where the authors propose involved sufficient criteria for rank-one convexity.
The latter requirement is due to the invariance of the singular value representation \(g(x,y)=h\big (\frac{x}{y}\big )+f(x \hspace{0.03em} y)\) under permutation of the arguments, which implies \(h\big (\frac{x}{y}\big )=h\big (\frac{x}{y}\big )\) for all \(x,y>0\).
The isotropy of the energy implies the symmetry under permutation of the two singular values \(\lambda _{1}\) and \(\lambda _{2}\), thus
$$ h(t)=h\bigg(\frac{\lambda _{1}}{\lambda _{2}}\bigg)=h\bigg( \frac{\lambda _{2}}{\lambda _{1}}\bigg)=h\bigg(\frac{1}{t}\bigg) \qquad \textit{for all}\quad t\in (0,\infty )\,. $$The equality \(h'(1)=0\) even holds for all \(h\in C^{1}((0,\infty ),\mathbb{R})\), since in that case,

The square root expression does not allow for a proper decoupling of \(h(t)\) and \(z(z)\), since
$$\begin{aligned} \sqrt{g_{xx}\,g_{yy}}&=\sqrt{\frac{1}{z^{2}}\left [2t^{3} \hspace{0.07em} h'(t)h''(t)+t^{4} \hspace{0.07em} h''(t)^{2}\right ]+\left [2t \hspace{0.07em} h'(t)+2t^{2} \hspace{0.07em} h''(t)\right ]f''(z)+z^{2}f''(z)^{2}} \\ &=\frac{1}{z}\sqrt{t^{2}h'(t)^{2}\,{-}\,t^{2}h'(t)^{2}\,{+}\,2t^{3} \hspace{0.07em} h'(t)h''(t)\,{+}\,t^{4} \hspace{0.07em} h''(t)^{2}\,{+}\,2\left [t \hspace{0.07em} h'(t)\,{+}\,t^{2} \hspace{0.07em} h''(t)\right ]z^{2}f''(z)\,{+}\,z^{4}f''(z)^{2}} \\ &=\frac{1}{z}\sqrt{\left [t \hspace{0.07em} h'(t)+t^{2} \hspace{0.07em} h''(t)+z^{2}f''(z)\right ]^{2}-t^{2}h'(t)^{2}}. \end{aligned}$$Here, \(\Psi \) is given by the representation \(W(F)=\psi \big (\mathbb{K}(F)\big )+f(\det F)\) of \(W\) with \(\psi \colon [1,\infty )\to \mathbb{R}\) and \(\mathbb{K}(F)=\frac{1}{2} \hspace{0.07em} \frac{\lVert F^{2} \rVert }{\det F}\). In our example, \(\psi (\mathbb{K})=e^{\frac{1}{10}\left [\operatorname{arcosh}\mathbb{K}(F) \right ]^{2}}\) and \(\psi '(\mathbb{K})=\frac{1}{5} \hspace{0.07em} e^{0.1\left [\operatorname{arcosh}\mathbb{K}(F)\right ]^{2}} \frac{\operatorname{arcosh}\mathbb{K}(F)}{\sqrt{\mathbb{K}^{2}-1}}\).
Here, \(\psi (\mathbb{K})=\frac{6}{5}\left (\mathbb{K}+\sqrt{\mathbb{K}^{2}-1}- \frac{1}{\mathbb{K}+\sqrt{\mathbb{K}^{2}-1}}\right )^{2}= \frac{24}{5}\left (\mathbb{K}^{2}-1\right )\) and \(\psi '(\mathbb{K})=\frac{48}{5} \hspace{0.07em} \mathbb{K}\).
The statement follows from the rank-one convexity of \(W\) and Lemma 3.2. Alternatively, the inequality \(t \hspace{0.07em} h''(t)+h'(t)>0\) can be shown directly by observing that \(h'(1)=0\) and \(h''(t)>0\) for all \(t\geq 1\) implies
$$\begin{aligned} h'(t)\geq 0 \quad \textit{for all}\ t\geq 1\qquad \implies \qquad t \hspace{0.07em} h''(t)+h'(t)>0\quad \textit{for all}\ t\geq 1\,. \end{aligned}$$For the case \(t<1\), we use the symmetry \(h(t)=h\big (\frac{1}{t}\big )\) and compute
$$\begin{aligned} h'(t)&=\frac{\mathrm{d}}{\mathrm{d}t} \hspace{0.07em} h(t)=\frac{\mathrm{d}}{\mathrm{d}t} \hspace{0.07em} h\left (\frac{1}{t}\right )=-\frac{1}{t^{2}} \hspace{0.07em} h'\left (\frac{1}{t}\right ), \\ h''(t)&=\frac{d^{2}}{dt^{2}} \hspace{0.07em} h(t)=\frac{d^{2}}{dt^{2}} \hspace{0.07em} h\left (\frac{1}{t}\right )=\frac{\mathrm{d}}{\mathrm{d}t}\left [- \frac{1}{t^{2}} \hspace{0.07em} h'\left (\frac{1}{t}\right )\right ]=\frac{2}{t^{3}} \hspace{0.07em} h'\left (\frac{1}{t}\right )+\frac{1}{t^{4}} \hspace{0.07em} h''\left (\frac{1}{t}\right ), \\ t \hspace{0.07em} h''(t)+h'(t)&=\frac{2}{t^{2}} \hspace{0.07em} h'\left (\frac{1}{t}\right )+\frac{1}{t^{3}} \hspace{0.07em} h''\left (\frac{1}{t}\right )-\frac{1}{t^{2}} \hspace{0.07em} h'\left (\frac{1}{t}\right )= \underbrace{\frac{1}{t^{2}}\hspace{0.07em}h'\left (\frac{1}{t}\right )}_{ \geq 0}+ \underbrace{\frac{1}{t^{3}}\hspace{0.07em}h''\left (\frac{1}{t}\right )}_{>0}>0 \quad \textit{for all}\ t< 1\,. \end{aligned}$$(3.9)Note that the infinitesimal isochoric term \(\lVert \operatorname{dev}_{2}\operatorname{sym}\xi \otimes \eta \rVert ^{2}=\frac{1}{2} \hspace{0.07em} \lvert \xi \rvert ^{2}\lvert \eta \rvert ^{2}\) is itself strictly rank-one convex.
References
Aguiar, A.R.: Strong ellipticity conditions for orthotropic bodies in finite plane strain. J. Elast. 134(2), 219–234 (2019)
Astala, K., Iwaniec, T., Martin, G.: Elliptic Partial Differential Equations and Quasiconformal Mappings in the Plane. Princeton University Press, Princeton (2008)
Aubert, G.: Necessary and sufficient conditions for isotropic rank-one convex functions in dimension 2. J. Elast. 39(1), 31–46 (1995)
Aubert, G., Tahraoui, R.: Sur la faible fermeture de certains ensembles de contraintes en elasticite non-lineaire plane. Arch. Ration. Mech. Anal. 97(1), 33–58 (1987)
Baker, M., Ericksen, J.L.: Inequalities restricting the form of the stress-deformation relation for isotropic elastic solids and Reiner-Rivlin fluids. J. Wash. Acad. Sci. 44, 33–35 (1954)
Ball, J.M.: Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63(4), 337–403 (1976)
Ball, J.M., Murat, F.: \(W^{1,p}\)-Quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58(3), 225–253 (1984)
Bertram, A., Böhlke, T., Šilhavỳ, M.: On the rank 1 convexity of stored energy functions of physically linear stress-strain relations. J. Elast. 86(3), 235–243 (2007)
Charrier, P., Dacorogna, B., Hanouzet, B., Laborde, P.: An existence theorem for slightly compressible materials in nonlinear elasticity. SIAM J. Math. Anal. 19(1), 70–85 (1988)
Ciarlet, P.G.: Mathematical Elasticity. Volume I: Three-Dimensional Elasticity. Studies in Mathematics and Its Applications, vol. 20. Elsevier, Amsterdam (1988)
Dacorogna, B.: Necessary and sufficient conditions for strong ellipticity of isotropic functions in any dimension. Discrete Contin. Dyn. Syst. 1(2), 257–263 (2001)
Dacorogna, B.: Direct Methods in the Calculus of Variations, 2nd edn. Applied Mathematical Sciences, vol. 78. Springer, Berlin (2008)
Dantas, M.J.H.: Equivalence between rank-one convexity and polyconvexity for some classes of elastic materials. J. Elast. 82(1), 1 (2006)
Davies, P.J.: A simple derivation of necessary and sufficient conditions for the strong ellipticity of isotropic hyperelastic materials in plane strain. J. Elast. 26(3), 291–296 (1991)
De Tommasi, D., Puglisi, G., Zurlo, G.: A note on strong ellipticity in two-dimensional isotropic elasticity. J. Elast. 109(1), 67–74 (2012)
Favrie, N., Gavrilyuk, S., Ndanou, S.: A thermodynamically compatible splitting procedure in hyperelasticity. J. Comput. Phys. 270, 300–324 (2014)
Federico, S.: Volumetric-distortional decomposition of deformation and elasticity tensor. Math. Mech. Solids 15(6), 672–690 (2010)
Flory, P.J.: Thermodynamic relations for high elastic materials. Trans. Faraday Soc. 57, 829–838 (1961)
Gavrilyuk, S., Ndanou, S., Hank, S.: An example of a one-parameter family of rank-one convex stored energies for isotropic compressible solids. J. Elast. 124(1), 133–141 (2016)
Ghiba, I.-D., Neff, P., Martin, R.J.: An ellipticity domain for the distortional Hencky logarithmic strain energy. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 471(2184), (2015) 20150510. https://doi.org/10.1098/rspa.2015.0510
Ghiba, I.-D., Neff, P., Šilhavỳ, M.: The exponentiated Hencky-logarithmic strain energy. Improvement of planar polyconvexity. Int. J. Non-Linear Mech. 71, 48–51 (2015). https://doi.org/10.1016/j.ijnonlinmec.2015.01.009
Ghiba, I.-D., Martin, R.J., Neff, P.: Rank-one convexity implies polyconvexity in isotropic planar incompressible elasticity. J. Math. Pures Appl. 116, 88–104 (2018)
Graban, K., Schweickert, E., Neff, P., Martin, R.J.: A commented translation of Hans Richter’s early work ‘The isotropic law of elasticity’. Math. Mech. Solids 24(8), 2649–2660 (2019). https://doi.org/10.1177/1081286519847495. Available at arXiv:1904.05164
Grabovsky, Y., Truskinovsky, L.: Legendre–Hadamard conditions for two-phase configurations. J. Elast. 123(2), 225–243 (2016)
Grabovsky, Y., Truskinovsky, L.: Explicit relaxation of a two-well Hadamard energy. J. Elast. 135, 351–373 (2019)
Grabovsky, Y., Truskinovsky, L.: When rank-one convexity meets polyconvexity: an algebraic approach to elastic binodal. J. Nonlinear Sci. 29(1), 229–253 (2019)
Hamburger, C.: A characterization for rank-one-convexity in two dimensions. Ric. Mat. 36, 171–181 (1987)
Hartmann, S., Neff, P.: Polyconvexity of generalized polynomial-type hyperelastic strain energy functions for near-incompressibility. Int. J. Solids Struct. 40(11), 2767–2791 (2003). https://doi.org/10.1016/S0020-7683(03)00086-6
Hencky, H.: Über die Form des Elastizitätsgesetzes bei ideal elastischen Stoffen. Z. Tech. Phys. 9, 215–220 (1928). Available at https://www.uni-due.de/imperia/md/content/mathematik/ag_neff/hencky1928.pdf
Horgan, C.O., Murphy, J.G.: On the volumetric part of strain-energy functions used in the constitutive modeling of slightly compressible solid rubbers. Int. J. Solids Struct. 46(16), 3078–3085 (2009)
Knowles, J.K., Sternberg, E.: On the ellipticity of the equations of nonlinear elastostatics for a special material. J. Elast. 5(3–4), 341–361 (1975)
Knowles, J.K., Sternberg, E.: On the failure of ellipticity of the equations for finite elastostatic plane strain. Arch. Ration. Mech. Anal. 63(4), 321–336 (1976)
Knowles, J.K., Sternberg, E.: On the failure of ellipticity and the emergence of discontinuous deformation gradients in plane finite elastostatics. J. Elast. 8(4), 329–379 (1978)
Martin, R.J., Ghiba, I.-D., Neff, P.: Rank-one convexity implies polyconvexity for isotropic, objective and isochoric elastic energies in the two-dimensional case. Proc. R. Soc. Edinb. A 147A, 571–597 (2017). Available at arXiv:1507.00266
Martin, R.J., Ghiba, I.-D., Neff, P.: A non-ellipticity result, or the impossible taming of the logarithmic strain measure. Int. J. Non-Linear Mech. 102, 147–158 (2018)
Martin, R.J., Ghiba, I.-D., Neff, P.: A polyconvex extension of the logarithmic Hencky strain energy. Anal. Appl. 17(3), 349–361 (2019). https://doi.org/10.1142/S0219530518500173. Available at arXiv:1712.08864
Martin, R.J., Voss, J., Ghiba, I.-D., Neff, P.: Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity. Proc. R. Soc. Edinb., Sect. A, Math. 150(5), 2620–2631 (2020). https://doi.org/10.1017/prm.2019.35. Available at arXiv:1903.00508
Martin, R.J., Voss, J., Ghiba, I.-D., Sander, O., Neff, P.: The quasiconvex envelope of conformally invariant planar energy functions in isotropic hyperelasticity. J. Nonlinear Sci. 30, 2885–2923 (2020). Available at arXiv:1901.00058
Merodio, J., Neff, P.: A note on tensile instabilities and loss of ellipticity for a fiber-reinforced nonlinearly elastic solid. Arch. Mech. 58(3), 293–303 (2006)
Mihai, L.A., Neff, P.: Hyperelastic bodies under homogeneous Cauchy stress induced by non-homogeneous finite deformations. Int. J. Non-Linear Mech. 89, 93–100 (2017). Available at arXiv:1608.05040
Mihai, L.A., Neff, P.: Hyperelastic bodies under homogeneous Cauchy stress induced by three-dimensional non-homogeneous deformations. Math. Mech. Solids 23(4), 606–616 (2018)
Montella, G., Govindjee, S., Neff, P.: The exponentiated Hencky strain energy in modeling tire derived material for moderately large deformations. J. Eng. Mater. Technol. 138(3), 1–12 (2016)
Murphy, J., Rogerson, G.: Modelling slight compressibility for hyperelastic anisotropic materials. J. Elast. 131(2), 171–181 (2018)
Ndanou, S., Favrie, N., Gavrilyuk, S.: Criterion of hyperbolicity in hyperelasticity in the case of the stored energy in separable form. J. Elast. 115(1), 1–25 (2014)
Ndanou, S., Favrie, N., Gavrilyuk, S.: The piston problem in hyperelasticity with the stored energy in separable form. Math. Mech. Solids 22(1), 101–113 (2017)
Nedjar, B., Baaser, H., Martin, R.J., Neff, P.: A finite element implementation of the isotropic exponentiated Hencky-logarithmic model and simulation of the eversion of elastic tubes. Comput. Mech. 62(4), 635–654 (2018). Available at arXiv:1705.08381
Neff, P., Ghiba, I.-D.: Loss of ellipticity for non-coaxial plastic deformations in additive logarithmic finite strain plasticity. Int. J. Non-Linear Mech. 81, 122–128 (2016). Available at arXiv:1410.2819
Neff, P., Ghiba, I.-D.: The exponentiated Hencky-logarithmic strain energy. Part III: coupling with idealized isotropic finite strain plasticity. Contin. Mech. Thermodyn. 28(1), 477–487 (2016). https://doi.org/10.1007/s00161-015-0449-y
Neff, P., Mihai, L.A.: Injectivity of the Cauchy-stress tensor along rank-one connected lines under strict rank-one convexity condition. J. Elast. 127(2), 309–315 (2017). Available at arXiv:1608.05247
Neff, P., Ghiba, I.-D., Lankeit, J.: The exponentiated Hencky-logarithmic strain energy. Part I: constitutive issues and rank-one convexity. J. Elast. 121(2), 143–234 (2015). https://doi.org/10.1007/s10659-015-9524-7
Neff, P., Lankeit, J., Ghiba, I.-D., Martin, R.J., Steigmann, D.J.: The exponentiated Hencky-logarithmic strain energy. Part II: coercivity, planar polyconvexity and existence of minimizers. Z. Angew. Math. Phys. 66(4), 1671–1693 (2015). https://doi.org/10.1007/s00033-015-0495-0
Neff, P., Eidel, B., Martin, R.J.: Geometry of logarithmic strain measures in solid mechanics. Arch. Ration. Mech. Anal. 222(2), 507–572 (2016). https://doi.org/10.1007/s00205-016-1007-x. Available at arXiv:1505.02203
Neff, P., Graban, K., Schweickert, E., Martin, R.J.: The axiomatic introduction of arbitrary strain tensors by Hans Richter–a commented translation of ‘Strain tensor, strain deviator and stress tensor for finite deformations’. Math. Mech. Solids 25(5), 1060–1080 (2020). Available at arXiv:1901.00058
Ogden, R.: Nearly isochoric elastic deformations: application to rubberlike solids. J. Mech. Phys. Solids 26(1), 37–57 (1978)
Parry, G.: On the planar rank-one convexity condition. Proc. R. Soc. Edinb., Sect. A, Math. 125(2), 247–264 (1995)
Pedregal, P.: What does rank-one convexity have to do with viscosity solutions? In: Trends in Applications of Mathematics to Mechanics, pp. 53–64 (2018)
Richter, H.: Das isotrope Elastizitätsgesetz. Z. Angew. Math. Mech. 28(7/8), 205–209 (1948)
Richter, H.: Verzerrungstensor, Verzerrungsdeviator und Spannungstensor bei endlichen Formänderungen. Z. Angew. Math. Mech. 29(3), 65–75 (1949). Available at https://www.uni-due.de/imperia/md/content/mathematik/ag_neff/richter_deviator_log.pdf. ISSN: 1521-4001
Rosakis, P.: Ellipticity and deformations with discontinuous gradients in finite elastostatics. Arch. Ration. Mech. Anal. 109(1), 1–37 (1990)
Rosakis, P., Simpson, H.C.: On the relation between polyconvexity and rank-one convexity in nonlinear elasticity. J. Elast. 37(2), 113–137 (1994)
Sansour, C.: On the physical assumptions underlying the volumetric-isochoric split and the case of anisotropy. Eur. J. Mech. Solids 27(1), 28–39 (2008)
Schröder, J., Neff, P.: Poly-, Quasi- and Rank-One Convexity in Applied Mechanics. Springer, Berlin (2010). https://doi.org/10.1007/978-3-7091-0174-2
Schröder, J., von Hoegen, M., Neff, P.: The exponentiated Hencky energy: anisotropic extension and case studies. Comput. Mech. 61(6), 657–685 (2018)
Schweickert, E., Mihai, L.A., Martin, R.J., Neff, P.: A note on non-homogeneous deformation with homogeneous Cauchy stress for a strictly rank-one convex energy in isotropic hyperelasticity. Int. J. Non-Linear Mech. 119, 103282 (2020)
Sendova, T., Walton, J.R.: On strong ellipticity for isotropic hyperelastic materials based upon logarithmic strain. Int. J. Non-Linear Mech. 40(2), 195–212 (2005)
Sidoroff, F.: Un modèle viscoélastique non linéaire avec configuration intermédiaire. J. Méc. 13(4), 679–713 (1974)
Šilhavỳ, M.: The Mechanics and Thermodynamics of Continuous Media. Texts and Monographs in Physics, Springer, Berlin (1997)
Šilhavỳ, M.: On isotropic rank 1 convex functions. Proc. R. Soc. Edinb., Sect. A, Math. 129(5), 1081–1105 (1999)
Šilhavỳ, M.: An O(n) invariant rank 1 convex function that is not polyconvex. Theor. Appl. Mech. 28–29, 325–336 (2002)
Šilhavỳ, M.: Convexity conditions for rotationally invariant functions in two dimensions. In: Sequeira, A., da Veiga, H.B., Videman, J.H. (eds.) Applied Nonlinear Analysis, pp. 513–530. Springer, Berlin (2002)
Šilhavỳ, M.: On SO(n)-invariant rank 1 convex functions. J. Elast. 71(1–3), 235–246 (2003)
Simo, J.C.: A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition. Comput. Methods Appl. Mech. Eng. 68(1), 1–31 (1988)
Simpson, H.C., Spector, S.J.: On copositive matrices and strong ellipticity for isotropic elastic materials. Arch. Ration. Mech. Anal. 84(1), 55–68 (1983)
Walton, J.R., Wilber, J.P.: Sufficient conditions for strong ellipticity for a class of anisotropic materials. Int. J. Non-Linear Mech. 38(4), 441–455 (2003)
Zubov, L., Rudev, A.: An effective method of verifying Hadamard’s condition for a non-linearly elastic compressible medium. J. Appl. Math. Mech. 56(2), 252–260 (1992)
Acknowledgements
The work of I.D. Ghiba has been supported by a grant of the Romanian Ministry of Research and Innovation, CNCS–UEFISCDI, Project no. PN-III-P1-1.1-TE-2019-0348, Contract No. TE 8/2020, within PNCDI III.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Rank-One Convexity in Planar Linear Elasticity
For the convenience of the reader, we recall here the well-known computation for rank-one convexity conditions in planar linear isotropic elasticity. Since
is a quadratic expression in terms of the displacement gradient \(\nabla u\) and hence \(\frac{1}{2} \hspace{0.07em} D^{2}W^{\mathrm{lin}}(\nabla u). (H,H)=W^{\mathrm{lin}}(H)\), the energy \(W^{\mathrm{lin}}\) is rank-one convex if and only if \(W^{\mathrm{lin}}(\xi \otimes \eta )\geq 0\) for all \(\xi ,\eta \in \mathbb{R}^{2}\). We compute

where we used the equality

Therefore, due to the Cauchy-Schwarz inequality, the energy potential in planar isotropic linear elasticity is rank-one convex if and only if \(\mu \geq 0\) and \(\mu +\kappa \geq 0\), where \(\mu \) and \(\kappa \) represent the (planar) shear modulus and the bulk modulus, respectively. In terms of the first Lamé parameter \(\lambda =\kappa -\mu \), rank-one convexity is also equivalent to the conditions \(\mu \geq 0\) and \(2\mu +\lambda \geq 0\).
Since the rank-one convexity of the isochoric and the volumetric part of the energy potential in linear elasticity are determinedFootnote 11 by the signs of \(\mu \) and \(\kappa \), respectively, we find
whereas the volumetric part \(W_{\mathrm{vol}}^{\mathrm{lin}}\) is not necessarily elliptic by itself even if \(W^{\mathrm{lin}}\) is rank-one convex.
Appendix B: The Planar Hadamard Material
We linearize the planar Hadamard material
which does not exhibit an additive volumetric-isochoric split, but is stress-free in the reference configuration under the assumption that \(f'(1)=-\mu \). First, we compute

In order to continue with the linearization, we note that \((\operatorname{tr}H)^{2}-\operatorname{tr}(H^{2})=2 \hspace{0.07em} \det (H)\) for any \(H\in \mathbb{R}^{2\times 2}\) and

Therefore
so we compute

Note that \(\mu \) is indeed the infinitesimal shear modulus and that the infinitesimal Lamé-parameter is given by \(\lambda =f''(1)-\mu \). Together with the well-known decomposition

of the Frobenius norm of \(X\in \mathbb{R}^{2\times 2}\) into its deviatoric part and its trace part, we obtain

thus the infinitesimal bulk modulus is \(\kappa =f''(1)\). Overall,
where \(\varepsilon =\operatorname{sym}\nabla u\) denotes the infinitesimal strain.
Appendix C: The Planar Hadamard Material with Volumetric-Isochoric Split
Next, we linearize the planar isotropic energy
now with an additive volumetric-isochoric split, which is stress-free in the reference configuration if \(f'(1)=0\). We start with the expansion

note that
We also compute

and observe that \(\mu \) is the infinitesimal shear modulus, \(\lambda =f''(1)-\mu \) is the infinitesimal Lamé-parameter and \(\kappa =f''(1)\) the infinitesimal bulk modulus. Overall,
in terms of the infinitesimal strain \(\varepsilon =\operatorname{sym}\nabla u\).
Now, we consider the more general case
for some arbitrary smooth \(\psi \colon [1,\infty )\to \mathbb{R}\). Then the linearization of \(W\) is given by

Therefore, the infinitesimal shear modulus and bulk modulus are given by \(\mu =\psi '(1)\) and \(\kappa =f''(1)\), respectively.
Appendix D: Algebraic Characterization of Rank-One Convexity
In order to illustrate the extent to which our results simplify the test for rank-one convexity of energy functions with an additive volumetric-isochoric split compared to a more direct approach, we provide here some of our initial computations which did not utilize the specific singular value representation in (1.15).
Again, consider an energy function of the form
We compute the bilinear form of the second derivative:
Beginning with the second derivative of the volumetric part, we first find
Now, since

we obtain

The first derivative can equivalently be expressed as
since the Cayley-Hamilton Theorem yields

For the second derivative of the volumetric part, we therefore find

For a rank-one matrix \(H=\xi \otimes \eta \), using that \(\det (\xi \otimes \eta )=0\), we further obtain

Now, we turn our attention to the derivatives of the isochoric part, finding
and
We compute
as well as

since

by virtue of the Cayley-Hamilton Theorem and

Moreover,

and thus
Assuming again that \(H=\xi \otimes \eta \) is a rank-one matrix with \(\det (\xi \otimes \eta )=0\), we find
and
Thus, we have deduced
In conclusion
Finally, we consider the common representation of the isochoric part in terms of the distortion function \(\mathbb{K}\colon \operatorname{GL}^{\!+}(2)\to [1,\infty )\), cf. (2.41). More specifically, let \(\psi \colon [1,\infty )\to \mathbb{R}\) denote the uniquely determined function with
for all \(F\in \operatorname{GL}^{\!+}(2)\). Then
and thus
At this point, it seems unfeasible to continue with the approach outlined above. In particular, methods based on direct computations in terms of matrix-valued arguments instead of a singular value based representation appear to be highly unsuited for drawing any further conclusions regarding the rank-one convexity of \(W_{\mathrm{iso}}\) and \(W_{\mathrm{vol}}\), respectively.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Voss, J., Ghiba, ID., Martin, R.J. et al. Sharp Rank-One Convexity Conditions in Planar Isotropic Elasticity for the Additive Volumetric-Isochoric Split. J Elast 143, 301–335 (2021). https://doi.org/10.1007/s10659-021-09817-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-021-09817-9
Keywords
- Nonlinear elasticity
- Finite isotropic elasticity
- Constitutive inequalities
- Hyperelasticity
- Rank-one convexity
- Loss of ellipticity
- Legendre-Hadamard condition
- Volumetric-isochoric split
- Separate convexity
- Baker-Ericksen inequality