Gradient Damage Analysis of a Cylinder Under Torsion: Bifurcation and Size Effects

Abstract

In this work, an elastic-damage evolution analysis is carried out for a cylinder under torsion made of a material obeying a gradient damage model with softening. Both semi-analytical and asymptotic approaches are developed to analyze the elastic, axisymmetric and bifurcation stages. We show the existence of a fundamental branch where the damage field is asymmetric and localized within a finite thickness from the boundary. By minimizing a generalized Rayleigh quotient, the bifurcation time and modes are obtained as a function of the length scale $\epsilon =\ell /R$ involving a material internal length and the cylinder radius. We will then focus on these size effects by assuming that $\epsilon$ is a small parameter in an asymptotic setting. After justification, specific spatial and temporal rescaled variables are introduced for the boundary layer problem. It is shown that the axisymmetric damage evolution and the bifurcation are governed by two universal functions independent of the length scale. The simulation results obtained by the semi-analytical approach are formally justified by the asymptotic methods.

1 Introduction

Since the advent of gradient damage models [26], these phase-field methods are gaining popularity among the computational mechanics community to simulate fracture phenomena of various physical natures, see [22] for a quick overview. Considerable efforts have been made to better understand the behaviors of these models governed by variational principles. Initially, the energy functional being minimized is conceived as a regularized approximation to the variational approach to fracture [5, 8], where the vanishing parameter $\ell$ is purely numerical in nature [4]. Recently, it has been recognized that this parameter $\ell$ can also be interpreted as an internal length scale characteristic of the material, see [6, 9, 25, 32]. In [16, 35], a fundamental link has been established between the gradient damage models and Griffith’s fracture model. When $\ell$ is small compared to the characteristic size of the body, the temporal propagation of an existing phase-field crack is asymptotically governed by a Griffith-type law involving a generalized energy release rate $G^{\ell }$ and a corresponding fracture toughness $G_{\mathrm{c}}^{\ell }$. In [38], crack nucleation induced by stress concentrations is investigated numerically. The internal length $\ell$ introduces a size-effect in structural failure governed by a competition between the material strength and a Griffith toughness criterion.

In this paper, we will focus on more fundamental properties of gradient damage models and particularly on the possibility of bifurcation and the associated size-effects. In a unidimensional setting, a large body of literature has been devoted to the bifurcation and stability issues of the gradient damage models, see [3, 27,28,29] but also a quick summary in [22]. The uniqueness and stability properties of the initial elastic solution depend strongly on the damage constitutive functions in the energy functional. In general, the homogeneous damage field is more likely to become unstable and bifurcate to a localized solution for sufficiently long bars compared to the internal length. In [36], initiation of periodic crack array in a semi-infinite domain is studied following analytical and numerical approaches. The spatial distribution of cracks can be explained by bifurcation of a fundamental branch. Since the internal length is the only length scale in the problem, it is shown that the bifurcation time is proportional to $\ell ^{2}$, while the wavelength scales with $\ell$. The objective of this paper is to further explore bifurcation properties of the gradient damage models and the corresponding the size-effects.

In [11, 13], a multiscale echelon structure of semi penny-shaped cracks is observed under mixed mode I and III loading. In [37], the development of lance-like fracture facets is investigated for a cylinder under combined tensile and antiplane shear stresses. A mechanism of the combined growth of the parent and daughter cracks under mixed loading is suggested in [18, 30] to capture the formation of the echelon crack patterns. The most intriguing phenomena observed in these experiments are the presence of repetitive fracture patterns, which we believe can be explained by the bifurcation mechanism in gradient damage models. In [31], such phase-field models are used in the numerical simulation for mixed mode I and III problems. It is found that the echelon cracks can be captured only if the material internal length parameter is small compared to the structure dimension. In this paper, we propose a theoretical analysis of such formation of repetitive damage patterns by performing a bifurcation analysis of the gradient damage models. Instead of considering the full complex three-dimensional mixed-mode problem, which is beyond the scope of this study, we propose to analyze a simplified pure antiplane shear problem with a cylindrical bar subject to torsional loading. It will be shown that a periodic damage pattern can be formed according to the variational principles of gradient damage models.

The loading prescribed on the cylindrical bar is controlled by an increasing angle $t$ of torsion on the upper section of cylinder. Three elastic-damage evolution stages will be analyzed: elastic, axisymmetric and bifurcation, as indicated by the following diagram

The elastic stage is characterized by an identically zero damage while the displacement solution $\boldsymbol {u}^{\mathrm {F}}$ satisfies static equilibrium. The existence of this stage is conditioned by the choice of damage constitutive functions, see [22]. The variational damage criterion will be reached at a finite critical time $t=t_{\mathrm {c}}$. In the asymmetric stage, damage doesn’t depend on the angular variation and can be expressed by $\alpha =\alpha (r)$. This is the fundamental branch from which bifurcation possibilities will be explored. Similarly to the thermal shock problem, the damage solution in the fundamental branch is not spatially homogeneous, since the damage criterion is not satisfied everywhere in the domain. For the bifurcated solution, we are looking for an out-of-plane displacement field $u_{z}(r,\theta )\,\boldsymbol {e}_{3}$ independent of axial variable $z$. These approximations can be justified in the following settings

• We assume in this work that the length of cylinder $L$ is relatively small such that a two-dimensional analysis can be carried out. More precisely, as can be seen from the prescribed boundary conditions (1), the displacement is left free in the axial direction such that we only seek the displacement solutions of type $\boldsymbol {u}+w\boldsymbol {e}_{3}$ for arbitrary $w\in \mathbb{R}$. In such setting, it is known that for a circular section there is no out-of-plane warping displacement of the section [21]. We will show further that the axisymmetric damage solution also does not induce warping: at first approximation, damage remains translationally invariant along the axial direction.

• The boundary conditions for the damage variable are of Neumann type so that the damage does not explicitly depend on the axial variable.

In this paper, both the semi-analytical and asymptotic approaches are developed. In Sect. 2, we recall the main ingredients of gradient damage models and define the problem settings for the torsion problem. Section 3 is devoted to the semi-analytical approach, where the elastic-damage evolution problem is solved analytically without further physical approximations. Numerical methods are used when closed-form solutions cannot be obtained, hence the solutions are both analytical and numerical in nature. Using the variational principles of the gradient damage models, we show the existence of a fundamental branch where the damage field is asymmetric, localized in a finite crown and decreases monotonically from a maximum value at the boundary to zero with a finite thickness. The axisymmetric damage is solved and is expressed using the Bessel and Struve functions. Numerical results are presented to illustrate the influence of the length scale $\ell /R$. Torque evolution is also computed to characterize structural softening behavior of the cylinder.

The analysis of bifurcation from this fundamental branch is then performed. Similar to [36], bifurcated solutions follow a periodic localized damage pattern and are sought using a partial Fourier series in the circumferential direction characterized by a wave number. We then arrive at two energy minimization problems involving a generalized Rayleigh quotient: one at a fixed wave number that governs the bifurcated displacement and damage solutions, the other with respect to the wave number. The first problem is equivalent to a generalized eigenvalue problem where the smallest eigenvalue is to be determined. Using the finite element method for spatial discretization and numerical algorithms, the Rayleigh quotient is obtained as a function of time, wave number and the length scale $\ell /R$. On the one hand, numerical simulations suggest that the axisymmetric solution will always lose uniqueness at a time approaching $t_{\mathrm {c}}$ as $\ell /R$ becomes smaller. The wave number, on the other hand, appears to be inversely proportional to $\ell /R$. These two numerical observations are the main results of this paper, and call for a more formal derivation using the asymptotic approach.

In Sect. 4, the elastic-damage evolution problem is solved under the assumption that the length scale $\epsilon =\ell /R$ is small following an asymptotic approach. Using the perturbation technique and the boundary layer method, we construct an asymptotic approximation of the semi-analytical solution by using two rescaled spatial and temporal coordinates and by performing an asymptotic expansion with respect to $\epsilon$. It is shown that the axisymmetric damage solution can be expressed with the help of a universal function that does not explicitly depend on $\epsilon$. The influence of the length scale $\ell /R$ can be successfully explained by the introduced rescaled spatial and temporal variables. Comparison with the previous semi-analytical results shows satisfying agreements.

We then continue the asymptotic analysis for the bifurcation from the fundamental branch. By using the definition of the Rayleigh quotient and thanks to the variational nature of the formulation, the orders of magnitude of the bifurcated solutions can be obtained with respect to the small parameter $\epsilon$. We obtain again a universal expression for Rayleigh quotient that does not explicitly depend on $\epsilon$. Its temporal evolution is governed by that of the previous universal function. The asymptotic Rayleigh quotient varies monotonically from $\infty$ at the onset of damage initiation to 0, which shows the existence of a universal bifurcation time independent of $\epsilon$. The size-effects previously obtained by the semi-analytical approach are formally justified by the asymptotic method.

2 Gradient Damage Modeling

2.1 Variational Formulation

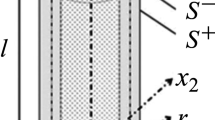
We consider a three-dimensional homogeneous and isotropic body whose natural reference configuration $\Omega$ is a straight cylinder of length $L$ with a cross circular section $S$ of radius $R$, see Fig. 1. Formally, we thus have

$$ \Omega =S\times [0,L]\,,\qquad S= \left \{(x,y)\in \mathbb{R}^{2}|x^{2}+y^{2}\leq R^{2}\right \}. $$

A frame of cylindrical coordinate system $(r,\theta ,z)$ along with its unit vectors $(\boldsymbol {e}_{r},\boldsymbol {e}_{\theta },\boldsymbol {e}_{3})$ is attached to the body $\Omega$. The lateral surface of the cylinder is stress-free

$$ \boldsymbol {\sigma }\boldsymbol {n}=\boldsymbol {0}\quad \text{on $\partial S\times (0,L)$}\,, $$

and the body is subject to the following displacements and stress conditions on the lower and upper cross sections

$$ \left \{ \begin{aligned} & u_{r}=u_{\theta }=0\quad \text{and}\quad \sigma _{33}=0 \quad \text{on $S\times \left \{0\right \}$}\,, \\ & u_{r}=0\,,\quad u_{\theta }=\mathit{tr}\quad \text{and}\quad \sigma _{33}=0 \quad \text{on $S\times \left \{L\right \}$}\,,\qquad \text{for $t\geq 0$}\,, \end{aligned} \right . $$

(1)

where $t$ denotes the increasing angle of torsion applied to the upper section and is regarded as a loading parameter. The geometric and boundary conditions of the cylinder under torsion is summarized in Fig. 1.

Fig. 1

Geometric and boundary conditions of the cylinder $\Omega =S\times [0,L]$ under torsion

The quasi-static structural evolution of the cylinder is described by the equilibrium state $(\boldsymbol {u},\alpha )$ of the displacement and damage fields at time $t$. We assume that at $t=0$ the body is at rest $\boldsymbol {u}_{0}=\boldsymbol {0}$ and the cylinder is undamaged $\alpha _{0}=0$. The evolution problem consists in finding $t\mapsto (\boldsymbol {u},\alpha )$ for all $0< t< t_{\mathrm{r}}$ where $t_{\mathrm{r}}$ corresponds to the onset of fracture, i.e., when $\max \alpha (\boldsymbol {x})=1$.

The cylinder is composed of a gradient-damage material. Its general formulation under a quasi-static setting is now recalled as follows. For a more complete physical and numerical overview, the interested readers are referred to [22, 26]. Contrary to a sharp interface description of cracks, the gradient damage approach introduces a continuous phase field replacing strong displacement discontinuities by strain localizations within a finite band. The damage parameter $\alpha$ is a scalar which can only grow from 0 to 1. It ensures a smooth transition between the undamaged state $\alpha =0$ and the crack $\alpha =1$, see Fig. 2(a).

Fig. 2

The discrete crack $\Gamma \subset \Omega$ is regularized by a continuous damage field $0\leq \alpha \leq 1$ in (a). The cross-section of the damage perpendicular to the phase-field crack is characterized by an optimal damage profile $\alpha _{*}$ indicated in (b) obtained with the damage constitutive model (14)

The evolution of such gradient-damage bodies is completely governed by variational arguments based on the definition of a total potential energy. Given the displacement and damage fields $(\boldsymbol {u},\alpha )$ belonging to appropriate functional spaces, the total potential energy is defined by

$$ \mathcal{P}(\boldsymbol {u},\alpha )=\int _{\Omega }W\bigl(\boldsymbol {\varepsilon }(\boldsymbol {u})( \boldsymbol {x}),\alpha (\boldsymbol {x}),\nabla \alpha (\boldsymbol {x})\bigr)\,\mathrm {d}\boldsymbol {x}\,, $$

(2)

where $W$ is the bulk energy density depending on the linearized strain tensor $\boldsymbol {\varepsilon }=\frac{1}{2}(\nabla \boldsymbol {u}+\nabla ^{\mathsf {T}}\boldsymbol {u})$, damage $\alpha$ and its gradient. This bulk energy density is the sum of two components: the stored elastic energy density and the dissipated energy density which quantifies the amount of energy consumed up to a damage state

$$W(\mathit{\epsilon },\alpha ,\mathrm{\nabla }\alpha )=\frac{1}{2}\mathsf{\text{A}}(\alpha )\mathit{\epsilon }\cdot \mathit{\epsilon }+w(\alpha )+w_1{\ell }^2\mathrm{\nabla }\alpha \cdot \mathrm{\nabla }\alpha .$$

(3)

• 1. The first term in (3) is the elastic energy density characterized by a damage-dependent elasticity tensor $\mathsf{\text{A}}(\alpha )$ which represents local stiffness degradation due to damage. The corresponding damage-dependent stress tensor reads $\mathit{\sigma }=\mathsf{\text{A}}(\alpha )\mathit{\epsilon }$. As in previous work, we assume that the Poisson’s ratio is unaffected by the damage variable, which leads to

  $$\mathsf{\text{A}}(\alpha )=\mathsf{a}(\alpha ){\mathsf{\text{A}}}_0,$$

  where $\alpha \mapsto \mathsf{a}(\alpha )$ denotes the non-dimensional stiffness degradation function with $\mathsf{a}(1)=0$, $\mathsf{a}(0)=1$.

• 2. The last two terms in (3) are the dissipated energy density, which introduces a length parameter $\ell$ that controls the damage band width from a geometric point of view (see Fig. 2). In (3), $\alpha \mapsto w(\alpha )$ represents another damage constitutive function representing the local damage dissipation during a homogeneous damage evolution and its maximal value $w(1)=w_{1}$ is the energy completely dissipated during such process when damage attains 1. Contrary to local strain-softening constitutive models, here the damage dissipation mechanism becomes non-local and localization is systematically accompanied by finite energy consumption, due to the presence of the gradient term, see [2, 3].

To properly define the total potential energy, the admissible functional spaces for $\boldsymbol {u}$ and $\alpha$ must be specified. Before final failure $t< t_{\mathrm{r}}$, the displacement field belongs to the classical Sobolev space $H^{1}(\Omega ,\mathbb{R}^{3})$ to ensure that the total potential energy that will be defined below is finite. The kinematically admissible space $\mathcal{C}_{t}$ takes into account the essential boundary conditions mentioned in (1). It is an affine space and its associated linear space is denoted by $\mathcal{C}_{0}$. Formally, they are respectively defined by

$$ \begin{aligned}[b] & \mathcal{C}_{t}= \left \{\boldsymbol {v}\in H^{1}(\Omega ,\mathbb{R}^{3})|v_{r}=v_{\theta}=0\quad \text{on $S\times \left \{0\right \}$}\,,\quad v_{r}=0\,,v_{\theta}=\mathit{tr}\quad \text{on $S\times \left \{L\right \}$}\right \} \,, \\ & \mathcal{C}_{0}= \left \{\boldsymbol {v}\in H^{1}(\Omega ,\mathbb{R}^{3})|v_{r}=v_{\theta}=0\quad \text{on $S\times \left \{0,L\right \}$}\right \}. \end{aligned} $$

(4)

Since damage is modeled as an irreversible defect evolution, its admissible space will be built from a current damage state $0\leq \alpha \leq 1$. Due to the presence of the damage gradient in the dissipated energy density (3), the above Sobolev space $H^{1}(\Omega ,\mathbb{R})$ is also used. Formally it is defined by

$$ \mathcal{D}(\alpha )= \left \{\beta \in H^{1}(\Omega ,\mathbb{R})|0\leq \alpha \leq \beta \leq 1\right \}. $$

(5)

It can be seen that a virtual damage field $\beta$ is admissible, if and only if it is accessible from the current damage state $\alpha$ verifying the irreversibility condition, i.e., the damage only grows. Consequently, the admissible space for the damage rate $\dot{\alpha }\in \dot{\mathcal{D}}$ is a convex cone and is given by

$$ \dot{\mathcal{D}}= \left \{\dot{\beta}\in H^{1}(\Omega ,\mathbb{R})|\dot{\beta}\geq 0\right \}. $$

(6)

With all variational ingredients set, the temporal evolution of the displacement and damage pair $t\mapsto (\boldsymbol {u}, \alpha )$ is governed by the following three physical principles

• 1. Irreversibility: the damage $t\mapsto \alpha$ is a non-decreasing function of time.

• 2. Meta-stability: the current state $(\boldsymbol {u},\alpha )$ is always directionally stable in the sense that for all admissible perturbations $\boldsymbol {v}\in \mathcal{C}_{0}$ and $\beta \in \dot{\mathcal{D}}$, there exists a $\overline{h}>0$ such that for all $h\in [0,\overline{h}]$ we have

  $$ (\boldsymbol {u}+h\boldsymbol {v},\alpha +h\beta )\in \mathcal{C}_{t}\times \mathcal{D}(\alpha )\,,\quad \mathcal{P}(\boldsymbol {u},\alpha )\leq \mathcal{P}(\boldsymbol {u}+h\boldsymbol {v},\alpha +h\beta ). $$

  (7)

• 3. Energy balance: the only energy dissipation is due to damage such that we have the following energy balance

  $$ \mathcal{P}(\boldsymbol {u},\alpha )=\mathcal{P}(\boldsymbol {u}_{0},\alpha _{0})+ \int _{0}^{t}\left (\int _{\Omega }\boldsymbol {\sigma }_{s}\cdot \boldsymbol {\varepsilon }(\dot{\boldsymbol {U}}_{s}) \,\mathrm {d}\boldsymbol {x}\right )\,\mathrm {d}s. $$

  (8)

In practice, the gradient-damage evolution problem is solved by invoking the first-order necessary conditions of the these physical principles. Interested readers are referred to [22] and references therein for detailed derivations based on variational reasoning. If the involved fields are sufficiently regular in space and in time, it can be shown that $\boldsymbol {u}$ satisfies the following static equilibrium equation

$$div\mathit{\sigma }=div(\mathsf{\text{A}}(\alpha )\mathit{\epsilon }(\mathit{u}))=0\text{ in }\mathrm{\Omega },$$

(9)

while $\alpha$ evolves according to the following damage criterion and consistency condition

$$\frac{1}{2}{\mathsf{\text{A}}}^{\prime }(\alpha )\mathit{\epsilon }(\mathit{u})\cdot \mathit{\epsilon }(\mathit{u})+w^{\prime }(\alpha )-2w_1{\ell }^2\mathrm{\Delta }\alpha \ge 0\text{ in }\mathrm{\Omega },\mathrm{\nabla }\alpha \cdot \mathit{n}\ge 0\text{ on }\partial \mathrm{\Omega },$$

(10)

$$(\frac{1}{2}{\mathsf{\text{A}}}^{\prime }(\alpha )\mathit{\epsilon }(\mathit{u})\cdot \mathit{\epsilon }(\mathit{u})+w^{\prime }(\alpha )-2w_1{\ell }^2\mathrm{\Delta }\alpha )\dot{\alpha }=0\text{ in }\mathrm{\Omega },(\mathrm{\nabla }\alpha \cdot \mathit{n})\dot{\alpha }=0\text{ on }\partial \mathrm{\Omega }.$$

(11)

These first order conditions are not sufficient for bifurcation and stability analysis for a given state $(\boldsymbol {u},\alpha )$, which requires the second-order directional derivatives of $\mathcal{P}$, see for instance [3, 29]. In the most general case, it is given by

$$\begin{array}{rcl}{\mathcal{P}}^{″}(\mathit{u},\alpha )(\mathit{v},\beta )& =& {\int }_{\mathrm{\Omega }}\mathsf{\text{A}}(\alpha )\mathit{\epsilon }(\mathit{v})\cdot \mathit{\epsilon }(\mathit{v})\mathrm{d}\mathit{x}+{\int }_{\mathrm{\Omega }}(\frac{1}{2}{\mathsf{\text{A}}}^{″}(\alpha )\mathit{\epsilon }(\mathit{u})\cdot \mathit{\epsilon }(\mathit{u})+w^{″}(\alpha )){\beta }^2\mathrm{d}\mathit{x}\\ & & +{\int }_{\mathrm{\Omega }}2{\mathsf{\text{A}}}^{\prime }(\alpha )\mathit{\epsilon }(\mathit{u})\cdot \mathit{\epsilon }(\mathit{v})\beta \mathrm{d}\mathit{x}+{\int }_{\mathrm{\Omega }}2w_1{\ell }^2\mathrm{\nabla }\beta \cdot \mathrm{\nabla }\beta \mathrm{d}\mathit{x}.\end{array}$$

(12)

2.2 Basic Properties of Gradient Damage Materials

We assume that the stiffness degradation function $\alpha \mapsto \mathsf{a}(\alpha )$ and the local damage dissipation function $\alpha \mapsto w(\alpha )$ verify certain physical properties which characterize the behavior of a strongly brittle material, see [27, Hypothesis 1]. During a homogeneous uniaxial traction experiment, it leads to the definition of the critical stress $\sigma _{\mathrm{c}}$ beyond which damage grows and the maximal stress that the material can sustain:

$${\sigma }_{\mathrm{c}}=\sqrt{\frac{2{\mathit{Ew}}^{\prime }(0)}{{\mathsf{\text{s}}}^{\prime }(0)}},{\sigma }_{\mathrm{m}}=\underset{\beta \in [0,1)}{max}\sqrt{\frac{2{\mathit{Ew}}^{\prime }(\beta )}{{\mathsf{\text{s}}}^{\prime }(\beta )}}.$$

(13)

In (13), $E$ denotes the Young’s modulus of the undamaged stiffness tensor ${\mathsf{\text{A}}}_0$.

The physical properties of the gradient damage model, in particular its softening or hardening character, directly depend on these two damage constitutive functions. An abundant literature is devoted to a theoretic or numerical analysis of these damage constitutive laws. The interested readers are referred to [17, 20, 22, 38] and references therein for a discussion on this point. In this contribution, the following damage constitutive model initially proposed in [26] is used

$$ \mathsf{a}(\alpha )=(1-\alpha )^{2}\,,\quad w(\alpha )=w_{1}\alpha . $$

(14)

If can be shown that damage does not evolve as long as a non-zero critical stress is not reached, a rather appreciated property when modeling brittle fracture. Then a strain-softening behavior is observed as damage grows for $\alpha \in (0,1)$, which implies that the critical stress coincides with the maximal stress. According to (13), during a unidimensional bar traction test we have

$$ \sigma _{\mathrm{c}}=\sigma _{\mathrm{m}}=\sqrt{w_{1}E}. $$

(15)

The damage dissipation energy density (last two terms) in (3) can be regarded as an equivalent Griffith crack surface functional density in phase-field models, see for example [23]. An effective fracture toughness $G_{\mathrm{c}}$, i.e., the energy required to create a unit Griffith-like crack surface, can be identified as the energy dissipated during the optimal damage profile creation in a uniaxial traction experiment, see [26] for a detailed discussion on this point. The optimal damage profile $\alpha _{*}$ can be considered as the theoretic cross-section perpendicular to a gradient-damage crack, see Fig. 2. If $x$ refers to the transverse coordinate axis centered at the crack where $\alpha _{*}(x)=1$, the optimal damage profile for the (14) model is given by

$$ \alpha _{*}(x)= \textstyle\begin{cases} \left (1-\frac{\left \lvert {x}\right \rvert }{2\ell }\right )^{2} & \text{if }\left \lvert {x}\right \rvert < 2\ell \,, \\ 0 & \text{else}. \end{cases} $$

(16)

It is also indicated in Fig. 2(b). With such optimal damage profile, the corresponding dissipated energy can be consequently computed by injecting $\alpha _{*}$ into (3) and then integrated along the cross-section, which leads to

$$ G_{\mathrm{c}}=4\ell \int _{0}^{1}\sqrt{w_{1}w(\beta )}\,\mathrm {d}\beta= \frac{8}{3}w_{1}\ell . $$

(17)

This equation prescribes a relation between the fracture toughness $G_{\mathrm{c}}$, the maximal damage dissipation $w_{1}$ and the internal length $\ell$.

3 Semi-Analytical Solutions

3.1 Purely Elastic Solution

By adopting the damage constitutive laws (14), the cylinder will first behave elastically with an identically zero damage field $\alpha =0$ when $t$ increases from 0. Due to static equilibrium (9) and the prescribed boundary conditions (1), the corresponding displacement field is unique up to an arbitrary constant axial translation in the $\boldsymbol {e}_{3}$ direction and its only nonzero component is the tangential displacement in the polar coordinate system

$$ \boldsymbol {u}^{\mathrm {F}}=\frac{\mathit{trz}}{L}\,\boldsymbol {e}_{\theta }. $$

(18)

In the sequel, $\boldsymbol {u}^{\mathrm {F}}$ denotes the fundamental displacement field from which perturbations in the sense of the meta-stability condition (7) will be then considered in Sect. 3.3. Its corresponding strain and stress fields in the cylinder are given by

$$ \boldsymbol {\varepsilon }^{\mathrm {F}}=\frac{\mathit{tr}}{2L}(\boldsymbol {e}_{\theta }\otimes \boldsymbol {e}_{z}+ \boldsymbol {e}_{z} \otimes \boldsymbol {e}_{\theta })\,,\quad \boldsymbol {\sigma }^{\mathrm {F}}= \frac{\mu _{0} \mathit{tr}}{L}(\boldsymbol {e}_{\theta }\otimes \boldsymbol {e}_{z}+\boldsymbol {e}_{z} \otimes \boldsymbol {e}_{\theta })\,, $$

(19)

where $\mu _{0}$ denotes the shear modulus of the sound material.

Due to the consistency condition (11), the elastic solutions (18)–(19) remain valid if the damage criterion (10) is satisfied with a strict inequality almost everywhere in the cylinder. Using the fundamental displacement field (18), with an identically zero damage field, (10) now reads

$$ \frac{\mu '(0)t^{2}r^{2}}{2L^{2}}+w'(0)\ge 0\,, $$

(20)

where $\mu (\alpha )=\mathsf{a}(\alpha )\mu _{0}$ denotes the shear modulus of a damaged material point. As $\mathsf{a}'(0)\leq 0$ and $w'(0)\geq 0$ (stiffness degradation and dissipation hypotheses, see [27]), the damage criterion (20) will be first attained (becomes an equality) on the lateral surface at $r=R$, i.e., on a subset of measure zero in $\mathbb{R}^{3}$. The corresponding time will be denoted by $t_{\mathrm {c}}$ (critical time) and is given by

$$ t_{\mathrm {c}}=\sqrt{-\frac{2w'(0)L^{2}}{\mu '(0) R^{2}}}. $$

For the damage constitutive law (14) used in this paper, with (17), the critical time thus reads

$$ t_{\mathrm {c}}=\sqrt{\frac{w_{1}L^{2}}{\mu _{0} R^{2}}}=\sqrt{ \frac{3G_{\mathrm{c}}L^{2}}{8\mu _{0}\ell R^{2}}}>0. $$

(21)

It can be verified that a non-zero elastic phase indeed exists in this case. The elastic phase is summarized in (22) for $0\leq t\leq t_{\mathrm {c}}$, with the fundamental displacement field given by (18) and a zero damage field. The subsequent gradient-damage evolution will be considered in Sect. 3.2.

(22)

3.2 Axisymmetric Damage Solution

From $t>t_{\mathrm {c}}$, the damage criterion (10)–(11) is gradually uniformly (in the $\boldsymbol {e}_{3}$ direction) and axisymmetrically (with respect to the $\theta$ coordinate) attained from the outer lateral surface $\partial S\times (0,L)$ into the cylinder. The main objective of this section is thus to analytically investigate the induced axisymmetric damage field $\alpha ^{\mathrm {F}}$ with the property

$$ \alpha (r,\theta ,z)=\alpha ^{\mathrm {F}}(r). $$

(23)

It can be shown that the associated displacement field is necessarily the fundamental displacement $\boldsymbol {u}^{\mathrm {F}}$ given by (18) and the associated stress and strain fields read as

$$ \boldsymbol {\varepsilon }^{\mathrm {F}}=\frac{\mathit{tr}}{2L}(\boldsymbol {e}_{\theta }\otimes \boldsymbol {e}_{z}+ \boldsymbol {e}_{z}\otimes \boldsymbol {e}_{\theta }),\quad \boldsymbol {\sigma }^{\mathrm {F}}= \frac{\mu (\alpha )\mathit{tr}}{L}(\boldsymbol {e}_{\theta }\otimes \boldsymbol {e}_{z}+\boldsymbol {e}_{z} \otimes \boldsymbol {e}_{\theta }). $$

Due to the fact that $\alpha$ only depends on $r$, the stress continues to verify the static equilibrium equation (9) and the prescribed boundary conditions (1). The axisymmetric damage phase is summarized in (24) for $t_{\mathrm {c}}< t\leq t_{*}$, with the fundamental displacement field given by (18) and the fundamental damage field.

(24)

In the sequel, we will make use of the derived damage evolution law (10)–(11) to solve the axisymmetric damage field for $t>t_{\mathrm {c}}$. Inserting the fundamental displacement field (18) into (10), we obtain the following damage criterion

$$ \mu '(\alpha )\frac{t^{2}r^{2}}{2L^{2}}+w'(\alpha )-2w_{1}\ell ^{2} \Delta \alpha \geq 0\qquad \text{for all $r\in [0,R)$.} $$

(25)

We suppose that the criterion (25) is reached with an equality within a radial thickness of $e$ at time $t$, see Fig. 3(a). Formally, the following subset of the cross-section $S^{\mathrm {d}}\subset S$ can be defined

$$ S^{\mathrm {d}}=[R-e,R)\times [0,2\pi )= \left \{(r,\theta )\in S|\mu '(\alpha )\frac{t^{2}r^{2}}{2L^{2}}+w'(\alpha )-2w_{1}\ell ^{2}\Delta \alpha =0\text{ with $z=\overline{z}$}\right \} \,, $$

(26)

where without loss of generality $\overline{z}\in (0,L)$ designates an arbitrary cross-section.

Fig. 3

Axisymmetric damage solution: (a) an illustration of the damage contour in an arbitrary section of the cylinder; (b) temporal evolution of the axisymmetric damage

To solve this second-order elliptic differential equation in $S^{\mathrm {d}}$, several additional conditions must be specified. On the one hand, according to (11), on the lateral surface $r=R$ where damage evolves the normal damage gradient must be zero. On the other hand, due to continuity of the damage field (implicitly contained in the variational formulation due to the presence of the damage gradient in the energy functional), it is equal to zero at the interface between the undamaged part and $S^{\mathrm {d}}$, see Fig. 3(b). Hence, we have

$$ \frac{\partial \alpha ^{\mathrm {F}}}{\partial r}(R)=0\,,\quad \alpha ^{\mathrm {F}}(R-e)=0. $$

(27)

Contrary to classical boundary value problems, here the boundary itself $S^{\mathrm {d}}$ is yet to be specified due to the unknown thickness parameter $e$. Moreover, in this case the boundary $S^{\mathrm {d}}$ (and thus the thickness) evolves with time as can be seen in Fig. 3(b). The determination of the thickness parameter $e$ requires hence another condition. It can be shown (see [15, 36] that the damage gradient is also continuous at the interface

$$ \frac{\partial \alpha ^{\mathrm {F}}}{\partial r}(R-e)=0. $$

(28)

This equation completes the previous boundary conditions (27) in order to solve the differential equation (26). In summary, with the chosen damage constitutive law (14), we arrive at the following system

$$ \left \{\textstyle\begin{array}{l} -\frac{\mu _{0}(1-\alpha )t^{2}r^{2}}{L^{2}}+w_{1}-2w_{1}\ell ^{2} \Delta \alpha =0\text{ in $[R-e, R)$}, \\ \frac{\partial \alpha ^{\mathrm {F}}}{\partial r}(R)=0\,,\quad \alpha ^{\mathrm {F}}(R-e)=0\,, \quad \frac{\partial \alpha ^{\mathrm {F}}}{\partial r}(R-e)=0. \end{array}\displaystyle \right . $$

(29)

We now propose a semi-analytical method to solve the unique axisymmetric damage field governed by the system (29) for $t\geq t_{\mathrm {c}}$. The Laplacian operator is now expressed in the cylindrical coordinate system, taking into account the axisymmetry of the damage field which is also constant in the $z$ direction. Written with the non-dimensional radial coordinate $\alpha ^{\mathrm {F}}(r)=d(\mathsf {r})=d(r/R)$, the differential equation (29) becomes

$$ \mathsf {r}d''(\mathsf {r})+d'(\mathsf {r})-\frac{1}{2}\left ( \frac{\mathit{tR}}{t_{\mathrm {c}}\ell }\right )^{2}\mathsf {r}^{3} d(\mathsf {r})= \frac{1}{2}\left (\frac{\mathit{tR}}{t_{\mathrm {c}}\ell }\right )^{2}\left (t_{\mathrm {c}}^{2} \mathsf {r}/t^{2}-\mathsf {r}^{3}\right ) \text{ for ${\Sigma }=\frac{R-e}{R}\leq \mathsf {r}< 1$}\,, $$

(30)

where the non-dimensional variable $\Sigma$ denotes the interface between the purely elastic region $\mathsf {r}<\Sigma$ and the region where the damage criterion (25) is attained with an equality. The general solution to (30) reads

$$ d(y)=1+C_{1} I_{0}(y)+C_{2} K_{0}(y)+ \frac{\pi t_{\mathrm {c}}R}{4\sqrt{2}t\ell }L_{0}(y)\,,\quad y= \frac{\mathit{tR}}{2\sqrt{2}t_{\mathrm {c}}\ell }\mathsf {r}^{2}\,, $$

(31)

where $I_{v}$ and $K_{v}$ are respectively the modified $v$-order Bessel function of the first kind and the second kind and $L_{v}$ is the modified $v$-order Struve function. Using the following identifies concerning the derivative of these special functions

$$ I_{0}'=I_{1}\,,\quad K_{0}'=-K_{1}\,,\quad L_{0}'=\frac{1}{2}\left ( \frac{2}{\pi }+L_{-1}+L_{1}\right ) $$

and the boundary conditions (27), the two constants $C_{1}$ and $C_{2}$ can be readily expressed as an explicit function of the thickness parameter $e$. Hence, the last boundary condition of (29) provides a nonlinear equation on $e$. The standard Newton-Raphson algorithm is applied to solve numerically this equation. The obtained damage solution is thus exact and semi-analytical in nature.

In Fig. 4(a), the damage thickness evolution is presented for three values of $\ell$ with respect to the normalized time scale $t/t_{\mathrm {c}}$. Due to irreversibility and in the absence of unloading, the thickness is strictly increasing. For smaller $\ell$, the damaged zone is also decreased at a fixed $t/t_{\mathrm {c}}$. The evolution is non-linear in general, however its initial slope near $t=t_{\mathrm {c}}$ seems to be independent of $\ell$. This property will be established in Sect. 4.

Fig. 4

Axisymmetric solutions: (a) damage thickness evolution; (b) damage solutions at $t/t_{\mathrm {c}}=1.1$; (c) torque evolution

At a fixed $t/t_{\mathrm {c}}=1.1$, the damage field along the radial direction $0\leq r\leq R$ for three internal lengths $\ell$ is shown in Fig. 4(b). The maximal damage on the lateral surface $r=R$ increases as the internal length $\ell$ decreases. It should be reminded that the critical time $t_{\mathrm {c}}$ at which damage begins depends itself on the internal length $\ell$, see (21).

The torque $M$ generated on the surface $z=L$ characterizes the global structural response of the cylinder under torsion. Using the stress vector $\boldsymbol {F}=\boldsymbol {\sigma }^{\mathrm {F}}\boldsymbol {e}_{3}$ on the section $S$ during the axisymmetric stage, the torque $M$ can be calculated by

$$ \begin{aligned}[b] M & =\boldsymbol {e}_{3}\cdot \int _{S} r\boldsymbol {e}_{r}\times \boldsymbol {F}\,\mathrm {d}\boldsymbol {s}= \int _{S} \frac{\mu (\alpha ^{\mathrm {F}})\mathit{tr}^{2}}{L}\,\mathrm {d}\boldsymbol {s}\\ & =\frac{2\pi \mu _{0} t}{L}\int _{0}^{R} a(\alpha ^{\mathrm {F}})r^{3}\,\mathrm {d}r= \frac{2\pi \mu _{0} t}{L}\left (\frac{(R-e)^{4}}{4}+\int _{R-e}^{R} a( \alpha ^{\mathrm {F}})r^{3}\,\mathrm {d}r\right ). \end{aligned} $$

(32)

Its evolution is illustrated in Fig. 4(c). For each $\ell$, it is normalized by its value $M_{\mathrm{c}}$ at $t=t_{\mathrm {c}}$. Similarly to damage thickness, its initial temporal rate of change appears to be a constant independently of $\ell$. During the axisymmetric stage, the moment first increases and reaches a maximal value. Afterwards the cylinder displays a structural softening behavior, where the moment decreases with $t$.

3.3 Bifurcation Analysis of the Fundamental Branch

The axisymmetric state $(\boldsymbol {u}^{\mathrm {F}},\alpha ^{\mathrm {F}})$ given respectively in (18) and (29) is obtained by considering only the first-order stability conditions (9), (10) and (11). This state is not guaranteed to remain always meta-stable and hence bifurcation may produce as the torsion angle $t$ increases. This section is thus mainly devoted to a bifurcation analysis of the axisymmetric state $(\boldsymbol {u}^{\mathrm {F}},\alpha ^{\mathrm {F}})$. Several stages of the complete evolution considered in this paper are recalled in (33) for $t_{*}< t< t_{\mathrm {r}}$, with $t_{\mathrm {r}}$ indicating the instant of fracture.

(33)

Although the axisymmetric solution in question is independent of the $z$ variable, the bifurcated state $(\boldsymbol {v},\beta )$ may be not. However, such full three dimensional analyses appear mathematically less tractable. Hence, in the sequel we will only seek the displacement field $\boldsymbol {u}$ in the following form

$$ \begin{aligned}[b] \boldsymbol {u} & =\boldsymbol {u}^{\mathrm {F}}(r,z)+\boldsymbol {u}^{\mathrm {B}}(r,\theta ) \\ & =\boldsymbol {u}^{\mathrm {F}}(r,z)+u^{\mathrm {B}}(r,\theta )\,\boldsymbol {e}_{3}\,, \end{aligned} $$

(34)

where $\boldsymbol {u}^{\mathrm {F}}\in \mathcal{C}_{t}$ is the fundamental displacement given by (18) and $\boldsymbol {u}^{\mathrm {B}}=u^{\mathrm {B}}(r,\theta )\,\boldsymbol {e}_{3}\in \mathcal{C}_{0}$ denotes the axial component regarded as the new unknown kinematic field. Due to static equilibrium (9), it can be shown that the damage field $\alpha$ is also independent of $z$

$$ \alpha =\alpha ^{\mathrm {F}}(r)+\alpha ^{\mathrm {B}}(r,\theta ). $$

(35)

By substituting (34) and (35) in the expression of the total potential energy (2), we obtain the new expression for our two-dimensional analysis

$$\begin{aligned} \mathcal{P}(\boldsymbol {u},\alpha ) =&L\widehat{\mathcal{P}}(u^{\mathrm {B}}, \alpha ) \\ =&L\int _{S}\left (\frac{1}{2}\mu (\alpha )\left (\nabla u^{\mathrm {B}}\cdot \nabla u^{\mathrm {B}}+\left (\frac{\mathit{tr}}{L}\right )^{2}+ \frac{2t}{L}\frac{\partial u^{\mathrm {B}}}{\partial \theta }\right )+w( \alpha )+w_{1}\ell ^{2}\nabla \alpha \cdot \nabla \alpha \right ) \,\mathrm {d}\boldsymbol {s}, \end{aligned}$$

(36)

where we recall that in a Cartesian coordinate system the derivative with respect to the tangential direction can be evaluated by

$$ \frac{\partial u^{\mathrm {B}}}{\partial \theta }(x,y)=-y\cdot \frac{\partial u^{\mathrm {B}}}{\partial x}(x,y)+x\cdot \frac{\partial u^{\mathrm {B}}}{\partial y}(x,y). $$

The stability and bifurcation properties of the gradient damage model require the second derivative (12) of the potential energy. Within the two-dimensional setting (34)–(35), the second derivative of the total potential energy (12) evaluated at the axisymmetric state $(\boldsymbol {u}^{\mathrm {F}},\alpha ^{\mathrm {F}})$ is a quadratic form in $(\boldsymbol {v},\beta )$ given by

$$ \mathcal{P}''(\boldsymbol {u}^{\mathrm {F}},\alpha ^{\mathrm {F}})(\boldsymbol {v},\beta )=L \widehat{\mathcal{P}}''(0,\alpha ^{\mathrm {F}})(v,\beta )=L\bigl(\mathsf{A}( \boldsymbol {v},\beta )-\mathsf{B}(\beta )\bigr)\,, $$

(37)

with $\mathsf{A}$ and $\mathsf{B}$ two quadratic forms defined respectively by

$$\begin{aligned} \mathsf{A}(v,\beta ) =& \int _{S}\left (\mu _{0}(1-\alpha ^{\mathrm {F}})^{2} \left (\frac{\partial v}{\partial r}\right )^{2}+\mu _{0}\left ( \frac{1-\alpha ^{\mathrm {F}}}{r}\frac{\partial v}{\partial \theta }-\frac{2\mathit{tr}}{L} \beta \right )^{2}+2w_{1}\ell ^{2}\nabla \beta \cdot \nabla \beta \right )\,\mathrm {d}\boldsymbol {s}\,, \\ \mathsf{B}(\beta ) =&\int _{S}3\mu _{0}\frac{t^{2}r^{2}}{L^{2}} \beta ^{2}\,\mathrm {d}\boldsymbol {s}, \end{aligned}$$

(38)

where the chosen damage constitutive law (14) is used. Note that $\boldsymbol {v}=v\,\boldsymbol {e}_{3}$ and $\beta$ represent a perturbation to the axisymmetric state $(\boldsymbol {u}^{\mathrm {F}},\alpha ^{\mathrm {F}})$.

The uniqueness of the axisymmetric solution can be analyzed by formulating the associated rate problem (see [3, 36]) which involves the following Rayleigh quotient

$$ \lambda =\mathsf{R}(v,\beta )= \textstyle\begin{cases} \frac{\mathsf{A}(v,\beta )}{\mathsf{B}(\beta )} & \text{if }\beta \neq 0\,, \\ +\infty & \text{otherwise.} \end{cases} $$

(39)

The current evolution $t\mapsto (\boldsymbol {u},\alpha )$ is unique, if the second derivative remains positive-definite

$$ \inf \lambda > 1 \text{ for all $(v,\beta )\in H^{1}(S)\times \mathcal{D}^{\mathrm {d}}(S)$} \,,\quad \mathcal{D}^{\mathrm {d}}(S)= \left \{\beta \in H^{1}(S)|\beta =0\text{ in $S\setminus S^{\mathrm {d}}$}\right \}\,, $$

(40)

where the set $\mathcal{D}^{\mathrm {d}}$ denotes the set of damage rates that remain zero in the undamaged part. The objective of the bifurcation analysis is to determine $t$ such that $\lambda =1$, i.e., when the current axisymmetric solution is no longer unique.

In this work, we will assume the following particular $(v,\beta )$ perturbations with 3 parameters $(k,A_{k},C_{k})$

$$ \begin{aligned}[b] v(r,\theta ) & =\sum _{k} A(r)\sin k\theta \,,\quad A\in H^{1}(0, 1) \equiv H^{1}, \\ \beta (r,\theta ) & =\sum _{k} C(r)\cos k\theta \,,\quad C\in \mathcal{D}^{\mathrm {d}}(0, 1)\equiv \mathcal{D}^{\mathrm {d}}, \end{aligned} $$

(41)

where $k\in \mathbb{N}^{*}$. In (41), the functions $A(r)$ and $C(r)$ represent the radial variation of $v$ and $\beta$, while the wave number $k$ characterizes the frequency of their angular variation. Note that at fixed $r$, the functions $v(r,\cdot )$ and $\beta (r,\cdot )$ are square-integrable continuous periodic functions, and can be well represented by the Fourier basis. The phase $\pi /2$ between $v$ and $\beta$ results in a natural coupling between them in the Rayleigh quotient.

Substituting (41) in (38) and using some basic integration properties of the trigonometric functions, the Rayleigh quotient now reads

$$ \lambda =\mathsf{R}(k,A,C)=\frac{\mathsf{A}(A,C)}{\mathsf{B}(C)}\,, $$

(42)

where at a fixed wave number $k$ the two quadratic forms $\mathsf{A}$ and $\mathsf{B}$ read

$$\begin{aligned} &\begin{aligned}[b] \mathsf{A}(A,C) = &\displaystyle \int _{0}^{R}\Biggl(2w_{1}\ell ^{2}\left (C^{\prime \,2}+ \frac{C^{2}k^{2}}{r^{2}}\right )+\mu _{0}(1-\alpha ^{\mathrm {F}})^{2}A^{\prime \,2} \\ &{}+\mu _{0} \left (\frac{1-\alpha ^{\mathrm {F}}}{r}\mathit{kA}-\frac{2\mathit{trC}}{L}\right )^{2}\Biggr)r \,\mathrm {d}r, \end{aligned} \\ & \mathsf{B}(C) =3\mu _{0}\frac{t^{2}}{L^{2}}\displaystyle \int _{0}^{R}r^{3}C^{2} \,\mathrm {d}r. \end{aligned}$$

(43)

To minimize (42), we will perform first the minimization with respect to $(A,C)$, and then to the wave number $k$

• 1. Minimization respect to $(A,C)$. Suppose that $(A_{k},C_{k})$ minimizes the Rayleigh ratio (42) at fixed $k\in \mathbb{N}^{*}$ with a minimum value $\lambda _{k}=\mathsf{R}(k,A_{k},C_{k})$. The corresponding necessary condition reads thus

  $$ \mathsf{A}'(A_{k},C_{k})(\hat{A},\hat{C})=\lambda _{k}\mathsf{B}'(C_{k}) \hat{C}\qquad \text{for all $(\hat{A},\hat{C})\in H^{1}\times \mathcal{D}^{\mathrm {d}}$}, $$

  (44)

  where $\mathsf{A}'$ and $\mathsf{B}'$ denotes the first directional derivative of $\mathsf{A}$ and $\mathsf{B}$ respectively. This equation corresponds to a generalized symmetric eigenvalue problem, where $\lambda _{k}$ is the smallest eigenvalue minimizing the Rayleigh quotient (42) and $(A_{k},C_{k})$ denotes the associated eigenvector.

• 2. Minimization with respect to $k\in \mathbb{N}^{*}$. Given $(A_{k},C_{k})$ the resulting minimizing eigenvector of the previous problem (44), the next step is to minimize the reduced Rayleigh quotient $k\mapsto \mathsf{R}(k,A_{k},C_{k})$, or equivalently the eigenvalue $\lambda _{k}$, for $k\in \mathbb{N}^{*}$. It consists of an integer optimization problem. The minimizing wave number is then referred to as the optimal wave number $k_{*}$. The minimum Rayleigh quotient evaluated at the optimal wave number $k_{*}$ will be denoted by

  $$ \lambda _{*}=\lambda _{k_{*}}=\mathsf{R}(k_{*}, A_{k_{*}}, C_{k_{*}}) \,,\quad k_{*}=\operatorname*{argmin}_{k} \mathsf{R}(k,A_{k},C_{k}). $$

  (45)

The eigenvalue problem and the minimization are solved numerically in Appendix.

For a specific internal length $\ell /R=0.1$, the $k$-dependence of the Rayleigh quotient $\lambda _{k}$ is illustrated in Fig. 5 for two values of torsion angles $t$. It can be seen that first at $t/t_{\mathrm {c}}=1.06$ the optimal wave number $k_{*}=5$ achieves the minimum of the Rayleigh quotient and then it shifts to $k_{*}=6$ when the minimum Rayleigh quotient $\lambda _{*}=1$, i.e., the instant when the axisymmetric solution is no longer unique.

Fig. 5

Rayleigh quotient $\lambda _{k}$ as a function of the wave number $k$ for $\ell /R=0.1$: (a) at $t/t_{\mathrm {c}}=1.06$; (b) at $t/t_{\mathrm {c}}\approx 1.149$

First let us take a look at the optimal $(v_{*},\beta _{*})$ perturbations for $\ell /R=0.1$ at $t/t_{\mathrm {c}}\approx 1.149$. They are optimal in the sense that they are evaluated with the optimal wave number $k_{*}$. The corresponding eigenfunctions $(A_{*},C_{*})$ are illustrated in Fig. 6.

Fig. 6

The optimal eigenfunctions with $k_{*}=6$ for $\ell /R=0.1$ at $t/t_{\mathrm {c}}\approx 1.149$: (a) normalized $A$; (b) normalized $C$

The eigenfunctions $(A_{*},C_{*})$ can not be normalized separately, we have thus normalized $(A_{*},C_{*})$ such that the rescaled $\tilde{A}(R)=1$. We observe that using the same normalization coefficient, the rescaled $\tilde{C}(R)$ is strictly larger than $\tilde{A}(R)$. This property will be established in Sect. 4. The function $A$ is non-zero almost everywhere in the whole radial direction $0< r\leq R$ while the function $C$ is non-zero only in the damaged part for $r>R-e$. This originates from the space definitions (41).

For a smaller internal length $\ell /R=0.05$, the $k$-dependence of the Rayleigh quotient as well as the optimal perturbation function $\tilde{v}$ at the instant of bifurcation $\lambda _{*}=1$ for $t/t_{\mathrm {c}}\approx 1.073$ are presented in Fig. 7. Compared to $\ell /R=0.1$, a larger optimal wave number $k_{*}=11$ is found for $\ell /R=0.05$. Also, the instant of bifurcation $t_{*}/t_{\mathrm {c}}$ is also decreasing.

Fig. 7

Bifurcation analysis for $\ell /R=0.05$ at $t/t_{\mathrm {c}}\approx 1.073$: (a) Rayleigh quotient $\lambda _{k}$ as a function of the wave number $k$; (b) the optimal normalized perturbation function $\tilde{v}$ with $k_{*}=11$

For $\ell /R=0.05$ and $\ell /R=0.1$, the time dependence of the optimal wave number $k_{*}$ and that of the minimum Rayleigh quotient $\lambda _{*}$ are presented in Fig. 8, where the observations above are clearly illustrated. In Fig. 8(a), while the optimal wave number $t\mapsto k_{*}$ is not constant after damage initiation, its variation is minimal ($\pm 1$ in the current time interval) and in any case we are only interested in its value at the instant of bifurcation when $\lambda _{*}=1$. In Fig. 8(b), we can see the optimal Rayleigh quotient gradually decreases with time. The bifurcation time can be identified when $\lambda _{*}=1$.

Fig. 8

Time dependence of the Rayleigh minimization problem for $\ell /R=0.05$ and $\ell /R=0.1$: (a) optimal wave number $k_{*}$; (b) minimum Rayleigh quotient $\lambda _{*}$

The instant of bifurcation $t_{\mathrm{b}}/t_{\mathrm {c}}$ and the optimal wave number $k_{*}$ are presented with respect to $\ell /R$ in Fig. 9. It illustrates size-dependance of bifurcation and will be analytically studied in Sect. 4. On the one hand, $t_{*}/t_{\mathrm {c}}$ scales linearly with the length scale $\ell /R$. In particular, for vanishing non-zero internal length $\ell \to 0^{+}$ the bifurcation takes place just after damage initiation $t_{*}\to t_{\mathrm {c}}$. On the other hand, $k_{*}$ scales inversely proportional with the length scale $\ell /R$ in particular for small $\ell /R$. These two properties illustrate the size-dependance of bifurcation and will be theoretically studied in Sect. 4.

Fig. 9

Size effect of bifurcation: (a) bifurcation time $t_{*}/t_{\mathrm {c}}$; (b) optimal wave number $k_{*}$

4 Asymptotic Behaviors for Small Internal Lengths

In the asymptotic approach, the internal length $\ell$ is assumed to be a small parameter compared to the cylinder radius $R$ in an asymptotic setting. The perturbation analysis is justified for the two following reasons:

• 1. The differential equation of asymmetric damage (30) involves a small coefficient $\ell$ in front of the highest order derivative, which suggests a boundary layer analysis similar to [1, 34].

• 2. In the bifurcation problem (or more precisely the eigenvalue problem) (44), the linear operators contain this small parameter $\ell$, which also calls for eigenvalue expansion analysis like [10, 12].

Therefore we investigate the elastic-damage problem in the neighborhood of the boundary $r=R$ by applying a zoom in space. A corresponding time rescaling is then carried out. The asymptotic analysis of the bifurcated solution from the fundamental solution is then performed for the boundary layer problem with respect to the small parameter. Finally, the bifurcation time and the wave number is then deducted from this analysis. For more references and applications of asymptotic method, we refer the reader to [39] for applications of this technique in fluid mechanics, [7, 24] for general boundary value problems and [1, 34] for solid mechanics applications.

Following the work of [35], we consider in this work that the radial thickness $e$ of the damaged region is of order $\ell$. With this hypothesis, the following non-dimensional variables are introduced

$$ \epsilon =\sqrt{2}\frac{\ell }{R}\ll 1,\quad \zeta = \frac{1-\mathsf {r}}{\epsilon }=\mathcal{O}(1)\geq 0, $$

(46)

where $\epsilon$ is the small parameter in our asymptotic analysis and $\zeta$ can be regarded as the new (stretched) spatial coordinate for the damage zone. Note that $\mathcal{O}(\epsilon ^{n})$ denotes a term of the order $\epsilon ^{n}$. Using this change of variable (46), we propose to analyze the asymptotic properties of damage evolution for small values of $\epsilon$.

4.1 Axisymmetric Damage Solution

We will first introduce a new loading parameter $\mathsf {t}=\mathcal{O}(1)$ compatible with the spatial coordinate $\zeta$ introduced in (46) by the following

Proposition 1

The new loading parameter $\mathsf {t}$ that governs damage evolution is defined by

$$ \mathsf {t}=\frac{1-t_{\mathrm {c}}/t}{\epsilon }=\mathcal{O}(1)\geq 0. $$

(47)

Proof

To prove the above relation, we perform asymptotic expansion in the damage region near the boundary $r=R$. Rewriting the axisymmetric equation (30) using (46), we obtain

$$\begin{aligned} &-\frac{t^{2}}{t_{\mathrm {c}}^{2}}\epsilon ^{2}\bigl(1-d(\zeta )\bigr)(1-3 \epsilon \zeta + \cdots )+1-\epsilon \zeta -\bigl((1-\epsilon \zeta )d''( \zeta )-\epsilon d'(\zeta )\bigr)+\mathcal{O}(\epsilon ^{2})=0\,, \\ &\quad \forall \zeta \in (0,\Sigma _{\zeta }), \end{aligned}$$

(48)

where $\Sigma _{\zeta }$ is the interface $\Sigma$ in (30) expressed in the stretched variable $\zeta$

$$ \Sigma _{\zeta }=\frac{1-\Sigma }{\epsilon }. $$

(49)

The boundary conditions in (29) are also rewritten using the new spatial variable $\zeta$, leading to

$$ d'(0)=0\,,\quad d'(\Sigma _{\zeta })=d(\Sigma _{\zeta })=0. $$

(50)

We assume an asymptotic expansion of damage field $d(\mathsf {r})$ in the form

$$ d(\mathsf {r})=d_{0}(\zeta )+\epsilon \cdot d_{1}(\zeta )+\cdots $$

(51)

Inserting (51) into (48), we obtain at order $\mathcal{O}(1)$

$$ d_{0}''(\zeta )-\frac{t^{2}}{t_{\mathrm {c}}^{2}}{d_{0}(\zeta )}=1- \frac{t^{2}}{t_{\mathrm {c}}^{2}}\Longrightarrow d_{0}(\zeta )=A\cosh \zeta +B \sinh \zeta +1-\frac{t_{\mathrm {c}}^{2}}{t^{2}}, $$

where $A$ and $B$ are two constants. Using the boundary conditions $d_{0}'(0)=d_{0}'(\Sigma _{\zeta })=0$ derived from (50), we obtain $A=B=0$, which implies

$$ d_{0}(\zeta )=1-\frac{t_{\mathrm {c}}^{2}}{t^{2}}. $$

But the above expression do not verify the another boundary condition $d_{0}(\Sigma _{\zeta })=0$. We conclude hence that $d_{0}=\mathcal{O}(\epsilon )$ and we deduce that

$$ 1-\frac{t_{\mathrm {c}}}{t}=\mathcal{O}(\epsilon ). $$

The proposed loading parameter (47) is thus justified. □

Using the new loading parameter (47) in (48), we obtain thus

$$\begin{aligned} &\bigl(1-d(\zeta )\bigr)\bigl(-1+\epsilon (-2\mathsf {t}+3\zeta +\cdots ) \bigr)+1-d''(\zeta )+\epsilon \bigl(-\zeta +d''(\zeta )+d'(\zeta ) \bigr)+\mathcal{O}(\epsilon ^{2})=0 \\ &\,,\quad \forall \zeta \in (0, \Sigma _{\zeta }). \end{aligned}$$

(52)

With the asymptotic expansion (51)), the differential equations at order $\epsilon ^{0}$ and $\epsilon$ are given by

$$\begin{aligned} & \text{At order $\epsilon ^{0}$:}\qquad d_{0}''(\zeta )-d_{0}(\zeta )=0 \,, \end{aligned}$$

(53)

$$\begin{aligned} & \text{At order $\epsilon ^{1}$:}\qquad d_{1}''(\zeta )-d_{1}(\zeta )+(2 \mathsf {t}-3\zeta )\bigl(1-d_{0}(\zeta )\bigr)+\zeta -d_{0}''-d_{0}'=0, \end{aligned}$$

(54)

with $d_{0}(\zeta )$ and $d_{1}(\zeta )$ satisfying the boundary conditions (50)). This leads to

$$ \begin{aligned}[b] & d_{0}(\zeta )=0\,, \\ & d_{1}''(\zeta )-d_{1}(\zeta )-2\zeta +2\mathsf {t}=0. \end{aligned} $$

(55)

The interface $\Sigma$ can be written with the new loading parameter $\mathsf {t}$ as

$$ \Sigma =1-\epsilon \cdot \mathsf {f}(\mathsf {t})+\mathcal{O}(\epsilon ^{2})\,, \quad \Sigma _{\zeta }=\mathsf {f}(\mathsf {t})=\mathcal{O}(1)\,, $$

(56)

where $\mathsf {f}(\mathsf {t})$ is positive by construction and is a universal function in the sense that it does not depend on the internal length $\ell$. The normalized thickness is hence given by

$$ \mathsf {e}=\frac{e}{R}=1-\Sigma =\epsilon \cdot \mathsf {f}(\mathsf {t})+ \mathcal{O}(\epsilon ^{2}). $$

(57)

After calculation, we obtain the following expressions for damage

$$\begin{aligned} d(\zeta ) & = 2\epsilon \left (\bigl(\mathsf {f}(\mathsf {t})-\mathsf {t}\bigr) \cosh \bigl(\mathsf {f}(\mathsf {t})-\zeta \bigr)-\sinh \bigl(\mathsf {f}(\mathsf {t})- \zeta \bigr)-\zeta +\mathsf {t}\right )+\cdots \,, \end{aligned}$$

(58)

$$\begin{aligned} d'(\zeta ) & = 2\left (\bigl(\mathsf {f}(\mathsf {t})-\mathsf {t}\bigr)\sinh \bigl(\mathsf {f}(\mathsf {t})-\zeta \bigr)-\cosh \bigl(\mathsf {f}(\mathsf {t})-\zeta \bigr)+1\right )+\cdots \,, \end{aligned}$$

(59)

where the universal function $\mathsf {f}(\mathsf {t})$ defined by (56) is governed by

$$ \bigl(\mathsf {t}-\mathsf {f}(\mathsf {t})\bigr)\sinh \mathsf {f}(\mathsf {t})+\cosh \mathsf {f}( \mathsf {t})=1. $$

(60)

Remark 1

Using the rescaled spatial (46) and temporal (47) variables, the asymptotic axisymmetric damage solution (58) does not explicitly depend on the small parameter $\epsilon$ aside from the multiplication factor. The temporal evolution of the axisymmetric damage can be directly explained by $\mathsf {t}$ and the universal function $\mathsf {f}(\mathsf {t})$.

Since no-closed form solution $\mathsf {f}(\mathsf {t})$ can be obtained from the nonlinear equation (60), it is solved numerically as a function of $\mathsf {t}$ in Fig. 10. On the one hand, it can be easily shown that

$$ \mathsf {f}(\mathsf {t})\approx 2\mathsf {t}\quad \text{for $\mathsf {t}\approx 0$}. $$

(61)

On the other hand, using the asymptotic behaviors $\cosh (\mathsf {f})\sim \exp (\mathsf {f})/2$ and $\sinh (\mathsf {f})\sim \exp (\mathsf {f})/2$ valid for larger $\mathsf {t}\gg 1$, we have

$$ \mathsf {f}(\mathsf {t})\approx 1+\mathsf {t}-2\exp \bigl(-\mathsf {f}(\mathsf {t})\bigr) \approx 1+\mathsf {t}\quad \text{for $\mathsf {t}\gg 1$}. $$

(62)

Fig. 10

Universal function $\mathsf {f}(\mathsf {t})$

Using (57) and (61), it can then be easily deduced that

$$ \dot{\mathsf {e}}(t)\equiv \frac{\mathrm {d}\mathsf {e}}{\mathrm {d}t}(t)= \frac{\mathrm {d}\mathsf {f}}{\mathrm {d}\mathsf {t}}(\mathsf {t})\cdot \frac{t_{\mathrm {c}}}{t^{2}}\Longrightarrow \dot{\mathsf {e}}(t_{\mathrm {c}})=2\,, $$

(63)

which formally proves that the normalized thickness evolves independently of the internal length at the onset of damage initiation. This result agrees well with our previous semi-analytical result in Fig. 4. The comparison with the asymptotic thickness (57) is presented in Fig. 11(a). The approximation is excellent even for moderate values of $\epsilon$ especially for $t/t_{\mathrm {c}}\to 1$.

Fig. 11

Comparison between the semi-analytical (exact) axisymmetric solutions and the asymptotic approach: (a) damage thickness evolution; (b) damage solutions at $t/t_{\mathrm {c}}=1.1$; (c) torque evolution; (d) maximum values of the torque

At fixed $t/t_{\mathrm {c}}$, the asymptotic behavior of the damage thickness can be analyzed as follows. For small values of $\ell$, we have $\mathsf {t}\gg 1$, hence the approximation (62) applies, which gives

$$ \mathsf {e}=\frac{e}{R}\approx \epsilon \cdot \mathsf {f}(\mathsf {t})\approx \epsilon \left (1+\frac{1-t_{\mathrm {c}}/t}{\epsilon }\right )=1- \frac{t_{\mathrm {c}}}{t}+\epsilon . $$

(64)

This equation shows that at fixed $t/t_{\mathrm {c}}\gg 1$, the thickness value decreases as $\ell$ becomes smaller, in agreement with the semi-analytical result in Fig. 4(a).

In Fig. 11(b), the asymptotic damage solution (58) is compared to the previous semi-analytical solution (31). The approximation is also remarkable especially for smaller values of $\ell$.

At fixed $t/t_{\mathrm {c}}$, the damage value on the boundary $\alpha (R)$ is now analyzed with respect to $\ell$. Using (58) and the approximation (62) valid for small $\ell$, we have

$$ \alpha (R)\approx 2\epsilon \left (\bigl(\mathsf {f}(\mathsf {t})-\mathsf {t}\bigr)\cosh \bigl(\mathsf {f}(\mathsf {t})\bigr)-\sinh \bigl(\mathsf {f}(\mathsf {t}) \bigr)+\mathsf {t}\right )\approx 2\epsilon (\mathsf {t}-1)=2\left (1- \frac{t_{\mathrm {c}}}{t}-\epsilon \right )\,, $$

(65)

which shows that $\alpha (R)$ increases for smaller values of $\ell$, at fixed $t/t_{\mathrm {c}}$. This result is in agreement with the semi-analytical results in Fig. 4(b).

Using the asymptotic approximation (58), the torque initially defined by (32) becomes

$$ M=\frac{\pi \mu _{0} \mathit{tR}^{4}}{2L}\left (1+8\epsilon ^{2}\bigl(\mathsf {f}( \mathsf {t})^{2}-2\mathsf {f}(\mathsf {t})\cdot \mathsf {t}\bigr)+\mathcal{O}( \epsilon ^{3})\right ), $$

(66)

where we recall that $\mathsf {t}$ is related to $t$ by (46). It can be deduced in particular that for $t\approx t_{\mathrm {c}}$ ($\mathsf {t}\approx 0$), $M$ evolves linearly with $t$ and is independent of $\ell$. This result confirms our previous result presented in Fig. 4(c). The comparison between the semi-analytical and the asymptotic solutions is given in Fig. 11(c). Similar to previous comparisons, the approximation by the asymptotic solution is outstanding for smaller $\ell$.

In Fig. 11(d), the maximum values of the torque achieved during the axisymmetric stage are presented for the semi-analytical and the asymptotic solutions. As expected, the difference becomes smaller as $\ell$ is decreased. It is also confirmed that the maximum torque is decreasing for smaller values of $\ell$.

4.2 Bifurcation Analysis of the Fundamental Branch

In this subsection, we perform an asymptotic analysis of the bifurcation of the axisymmetric solution for small values of $\ell$. Our analysis will be based on the minimization of the Rayleigh quotient (40) with the particular perturbations assumed in (41).

To begin with, we will assume that the bifurcation time is compatible with the new rescaled time parameter defined in (47). This implies in particular that the Rayleigh quotient remains of order $\mathcal{O}(1)$ for smaller values of $\epsilon$ since at bifurcation we have necessarily $\lambda _{*}=1$.

$$ \frac{1-t_{\mathrm {c}}/t_{\mathrm{b}}}{\epsilon }=\mathcal{O}(1)\,,\quad \lambda _{k}=\mathcal{O}(1). $$

(67)

This assumption will be proven a posteriori.

The first step is to evaluate the relative orders of magnitude of $k$, $A_{k}$ and $C_{k}$ with respect to the small parameter $\epsilon$. Recall that they minimize the Rayleigh quotient, see (44) and (45). Since $A_{k}$ and $C_{k}$ are the solution to the eigenvalue problem (44), we can assume without the loss of generality

$$ A_{k}=\mathcal{O}(\epsilon ). $$

(68)

The orders of magnitude of $k$ and $C_{k}$ will be determined from this choice.

Proposition 2

Assuming (68), we have the following estimates

$$ k=\mathcal{O}(1/\epsilon )\,, \quad C_{k} =\mathcal{O}(1). $$

Proof

Let us rewrite $\mathsf{A}$ and $\mathsf{B}$ in (43) of the Rayleigh quotient (42) using the normalized radial coordinate $\mathsf {r}=r/R$

$$\begin{aligned} & \begin{aligned}[b] \mathsf{A}(A_{k},C_{k}) = \,& R^{2}\displaystyle \int _{0}^{1}\Biggl(w_{1}\epsilon ^{2} \left (C_{k}^{\prime \,2}+\frac{C_{k}^{2}k^{2}}{\mathsf {r}^{2}}\right )+ \frac{\mu _{0}}{R^{2}}(1-d(\mathsf {r}))^{2}A_{k}^{\prime \,2} \\ &{}+ \frac{\mu _{0}}{R^{2}}\left (\frac{1-d(\mathsf {r})}{\mathsf {r}}\mathit{kA}_{k}- \frac{2\mathit{tR}^{2}}{L}\mathsf {r}C_{k}\right )^{2}\Biggr)\mathsf {r}\,\mathrm {d}\mathsf {r}\,, \end{aligned} \\ & \mathsf{B}(C_{k}) =3\mu _{0}\frac{t^{2}R^{4}}{L^{2}}\displaystyle \int _{0}^{1} \mathsf {r}^{3}C_{k}^{2}\,\mathrm {d}\mathsf {r}. \end{aligned}$$

(69)

Focus on the gradient damage term in $\mathsf{A}$ involving explicitly the small parameter $\epsilon$. For this term to be of the same order as $C_{k}$ due to (67), we deduce immediately

$$ k=\mathcal{O}(1/\epsilon )\,,\quad (\cdot )'=\mathcal{O}(1/\epsilon ) \,, $$

(70)

where $(\cdot )'$ denotes the derivation operator with respect to $\mathsf {r}$. This second relation justifies the use of a stretched variable $\zeta$ introduced previously in (46).

We recall that $d(\mathsf {r})=\mathcal{O}(\epsilon )$ according to (58), hence it can be neglected with respect to 1. Due to the definition (68) and with (70), the terms in $\mathsf{A}(A_{k},C_{k})$ involving $A_{k}$ are thus of order $\mathcal{O}(1)$. By comparison with $\mathsf{B}(C_{k})$, this means also $C_{k} =\mathcal{O}(1)$. The proof is thus complete. □

Differential Equation for $A_{k}$ at Fixed $k\in \mathbb{N}^{*}$

Integrating by parts (44) with $\hat{C}=0$ rewritten in the normalized radial coordinate $\mathsf {r}=r/R$, we obtain the following differential equation governing $A_{k}$

$$\begin{aligned} & \mathsf {r}\left ( \mathsf {r}A_{k}'(\mathsf {r}) \right )'- \frac{2 d'(\mathsf {r}) }{1-d(\mathsf {r})}\mathsf {r}^{2}A_{k}'(\mathsf {r})-k^{2}A_{k}+ \frac{2\mathit{tR}^{2}k}{L}\mathsf {r}^{2}\frac{C_{k}}{1-d(\mathsf {r})}=0\quad \text{for $0< \mathsf {r}< 1$}, \end{aligned}$$

(71)

$$\begin{aligned} & A_{k}'(0)=A_{k}'(1)=0\,,\quad [\!\![{A_{k}}]\!\!](\Sigma )=0\,,\quad [\!\![{A_{k}'}]\!\!](\Sigma )=0 \,, \end{aligned}$$

(72)

where $[\!\![{\cdot}]\!\!]$ denotes the usual jump operator. Note that in the undamaged region for $\mathsf {r}< 1-\mathsf {e}\equiv \Sigma$, we have $d=\beta _{k}=0$ which implies also $C_{k}=0$. We have hence

$$ \mathsf {r}^{2}A_{k}''(\mathsf {r})+\mathsf {r}A_{k}'(\mathsf {r})-k^{2}A_{k}( \mathsf {r})=0\quad \text{for $0< \mathsf {r}< \Sigma $}. $$

(73)

Since $A_{k}$ is bounded, the solution to (73) is given by

$$ A_{k}(\mathrm {r})=\mathsf{C}\mathrm {r}^{k}\quad \text{for $0< \mathsf {r}< \Sigma $}, $$

(74)

where $\mathsf{C}$ is an arbitrary constant depending on $k$.

Differential Equation for $C_{k}$ at Fixed $k\in \mathbb{N}^{*}$

After integrating by parts (44) with $\hat{A}=0$ rewritten in the normalized radial coordinate $\mathsf {r}=r/R$, we obtain the weak equation for $C_{k}$, we obtain the differential equation governing $C_{k}$

$$\begin{aligned} & -\epsilon ^{2} \mathsf {r}\left (\mathsf {r}C_{k}'(\mathsf {r}) \right )'+ \left (\epsilon ^{2}k^{2} + \left (4-3\lambda _{k}\right ) \frac{t^{2}}{t_{c}^{2}} \mathsf {r}^{4} \right )C_{k}(\mathsf {r})-2 \frac{t}{t_{c}^{2}}\frac{L}{R^{2}} k\mathsf {r}^{2}\left ({1-d(\mathsf {r})} \right ){A_{k}}(\mathsf {r})=0 \\ &\quad \text{for $\Sigma \leq \mathsf {r}\leq 1$}, \end{aligned}$$

(75)

$$\begin{aligned} & C_{k} ({\Sigma })=0\,,\quad C_{k}'(1)=0. \end{aligned}$$

(76)

We recall that the equation is reduced to the damaged interval $(\Sigma , 1)$ due to the definition of $\mathcal{D}^{\mathrm {d}}$ in (40). We can see that the small parameter $\epsilon$ appears in the highest derivative. This singular perturbation problem requires a zoom at $\mathsf {r}=1$.

Asymptotic Analysis of Displacement and Damage Fields for Small Internal Lengths

Using (67) and Proposition 2, we seek the leading-order solutions to (71) and (75) for $\Sigma \leq \mathsf {r}\leq 1$ [10, 12]

$$\begin{aligned} \lambda _{k}=\Lambda +\cdots \,,\quad \frac{t_{\mathrm {c}}}{t_{\mathrm{b}}}=1- \epsilon \cdot \mathsf {t}_{*}\,,\quad k=\frac{\mathsf{k}}{\epsilon }+ \cdots \,,\quad A_{k}=\epsilon \cdot \mathsf{a}+\cdots \,,\quad C_{k}= \mathsf{c}+\cdots \end{aligned}$$

(77)

Using the stretched variables $\zeta$ and $\Sigma _{\zeta }$ defined respectively in (46) and (56) and the fact that $d(\mathsf {r})=\mathcal{O}(\epsilon )$ and $d'(\mathsf {r})=\mathcal{O}(1)$ according to (58) and (59), we obtain at leading order for $0\leq \zeta \leq \Sigma _{\zeta }$

$$ \begin{aligned}[b] & \mathsf{a}''(\zeta ) -\mathsf{k}^{2}\mathsf{a}(\zeta ) + \frac{2t_{c}R^{2}\mathsf{k}}{L}{\mathsf{c}(\zeta )}=0, \\ & - \mathsf{c}''(\zeta )+\left (\mathsf{k}^{2} +\left (4-3\Lambda \right )\right )\mathsf{c}(\zeta )-\frac{2 \mathsf{k} }{ t_{c}} \frac{L}{R^{2}}{\mathsf{a}(\zeta )}=0. \end{aligned} $$

(78)

We seek approximate solutions for $\mathsf{a}(\zeta )$ and $\mathsf{c}(\zeta )$ as a power series of $\zeta$

$$ \mathsf{a}(\zeta )=a_{0}+a_{1}\zeta +a_{2}\zeta ^{2}+a_{3}\zeta ^{3}+a_{4} \zeta ^{4}+\cdots \,,\quad \mathsf{c}(\zeta )=b_{0}+b_{1}\zeta +b_{2} \zeta ^{2}+b_{3}\zeta ^{3}+b_{4}\zeta ^{4}+\cdots $$

(79)

The boundary conditions (72) and (76) are now expressed using the stretched variables

$$ \mathsf{a}'(0)=0\,,\quad \mathsf{c}'(0)=0\,,\quad [\!\![{\mathsf{a}}]\!\!]( \Sigma _{\zeta })=0\,,\quad [\!\![{\mathsf{a}}]\!\!]'(\Sigma _{\zeta })=0\,, \quad \mathsf{c}(\Sigma _{\zeta })=0\quad \text{where $(\cdot )'=\frac{\mathrm {d}}{\,\mathrm {d}\zeta}$}. $$

(80)

Using the first two conditions of (80), we find immediately $a_{1}=b_{1}=0$. Substituting (79) into (78), we obtain $a_{3}=b_{3}=0$ and

$$ \begin{aligned}[b] & 2a_{2}-\mathsf{k}^{2}a_{0}=-\frac{2t_{c} \mathsf{k}R^{2}}{L}{b_{0}}, \quad -2b_{2}+\left (\mathsf{k}^{2} +\left (4-3\Lambda \right ) \right )b_{0}=\frac{2 \mathsf{k} }{ t_{c} }\frac{L}{R^{2}}{a_{0}}, \\ & 12a_{4} -\mathsf{k}^{2}a_{2}=-\frac{2t_{c} \mathsf{k}R^{2}}{L}{b_{2}}, \quad -12b_{4}+\left (\mathsf{k}^{2} +\left (4-3\Lambda \right ) \right )b_{2}=\frac{2 \mathsf{k} }{ t_{c} }\frac{L}{R^{2}}{a_{2}}. \end{aligned} $$

(81)

Using the remaining boundary conditions in (80) and the solution (74) in $\mathsf {r}\in (0,\Gamma )$, we obtain

$$ \begin{aligned}[b] a_{0}+a_{2} \Sigma _{\zeta }^{2}+a_{4}\Sigma _{\zeta }^{4}=\mathsf{C} \Sigma ^{\mathsf{k}/\epsilon },\quad 2a_{2}\Sigma _{\zeta }+4a_{4} \Sigma _{\zeta }^{3} =-\mathsf{k}\mathsf{C}\Sigma ^{\mathsf{k}/ \epsilon -1}\,,\quad b_{0}+b_{2}\Sigma _{\zeta }^{2}+b_{4}\Sigma _{ \zeta }^{4}=0\,, \end{aligned} $$

(82)

where $\mathsf{C}$ is the integration constant in (74) and $\Sigma _{\zeta }$ and $\Sigma$ are related by (49). Since $\epsilon$ is a small parameter, we have $\mathsf{k}/\epsilon -1\approx \mathsf{k}/\epsilon$ and (82) can be reduced to the following homogeneous system

$$ \begin{aligned}[b] & \mathsf{k}(a_{0}+a_{2}\mathsf {f}(\mathsf {t})^{2}+a_{4}\mathsf {f}(\mathsf {t})^{4})+2a_{2} \mathsf {f}(\mathsf {t})+4a_{4}\mathsf {f}(\mathsf {t})^{3}=0, \\ & b_{0}+b_{2}\mathsf {f}(\mathsf {t})^{2}+b_{4}\mathsf {f}(\mathsf {t})^{4}=0, \end{aligned} $$

(83)

where $\Sigma _{\zeta }$ is replaced by $\mathsf {f}(\mathsf {t})$ due to (56).

Using (81), the variables $(a_{2}, b_{2}, a_{4}, b_{4})$ can be expressed using a linear combination of $(a_{0}, b_{0})$. Hence, the only unknowns in the homogeneous system (83) are $(a_{0}, b_{0})$. It admits a non-trivial solution if and only if the determinant $J$ is zero, which is given by the following quadratic equation in $\Lambda$

$$ J=J\bigl(\mathsf {f}(\mathsf {t}),\mathsf{k},\Lambda \bigr)=P(\mathsf {f}(\mathsf {t}), \mathsf{k})\Lambda ^{2}+Q(\mathsf {f}(\mathsf {t}),\mathsf{k})\Lambda +R(\mathsf {f}( \mathsf {t}),\mathsf{k})=0\Longrightarrow \Lambda =\Lambda \bigl(\mathsf {f}(\mathsf {t}), \mathsf{k}\bigr)\,, $$

(84)

with $(P,Q,R)$ three polynomials involving different powers of $\mathsf {f}$ and $\mathsf{k}$ up to $\mathsf {f}(\mathsf {t})^{8}\mathsf{k}^{8}$. The Rayleigh quotient $\Lambda =\Lambda \bigl (\mathsf {f}(\mathsf {t}),\mathsf{k}\bigr )$ is thus the smaller positive solution to (84). Observe that the asymptotic Rayleigh quotient $\Lambda$ is not an explicit function of the time variable $t$ or $\mathsf {t}$. Its time-dependence is through the value of the universal function $\mathsf {f}(\mathsf {t})$. It is also a universal function in the sense that it also does not depend on the small parameter $\epsilon$. Its effective $\epsilon$-dependence is explained by the rescaled time variable $\mathsf {t}$. The optimal asymptotic wave number $\mathsf{k}_{*}$ can be obtained by minimizing $\Lambda$ at fixed $\mathsf {f}(\mathsf {t})$.

$$ \frac{\partial \Lambda }{\partial \mathsf{k}}\bigl(\mathsf {f}(\mathsf {t}), \mathsf{k}_{*}\bigr)=0. $$

(85)

Using $\mathsf{k}_{*}$, we obtain thus the optimal Rayleigh quotient $\Lambda _{*}(\mathsf {t})=\Lambda \bigl (\mathsf {f}(\mathsf {t}),\mathsf{k}_{*} \bigr )$.

We can show that for $\mathsf {t}\approx 0$, the Rayleigh quotient is given by

$$ \Lambda =\frac{2-2\sqrt{3}/3}{\mathsf {f}(\mathsf {t})^{2}}+\frac{4}{3}+ \frac{\mathsf{k}^{2}}{3}+\mathcal{O}(\mathsf {f}(\mathsf {t})\cdot \mathsf{k}) \,, $$

(86)

which shows that for $\mathsf {t}\to 0$, we have $\mathsf{k}_{*}\to 0$ while $\Lambda _{*}\to \infty$. For $\mathsf {t}\to \infty$, we have

$$ \Lambda =\frac{\mathsf{k}^{2}}{3}+\mathcal{O}\left ( \frac{1}{\mathsf {f}(\mathsf {t})^{2}}\right )\,, $$

(87)

which implies $\mathsf{k}_{*}\to 0$ and $\Lambda _{*}\to 0$ for $\mathsf {t}\to \infty$. The optimal wave number and the Rayleigh quotient are presented in Fig. 12, which confirms (86) and (87).

Fig. 12

Universal asymptotic optimal Rayleigh quotient $\Lambda _{*}$ as well as the optimal asymptotic wave number $\mathsf{k}_{*}$

Remark 2

The limiting behaviors of the asymptotic Rayleigh quotient (86) and (87) actually confirms the previous assumption (67): the bifurcation time is actually a constant using the rescaled loading parameter (47), which implies $\lambda _{k}=\mathcal{O}(1)$.

The universal bifurcation time written using the variable $\mathsf {t}$ can be obtained by solving $\Lambda _{*}(\mathsf {t}_{*})=1$, which leads to

$$ f(\mathsf {t}_{*})\approx 1.685\Longrightarrow \mathsf {t}_{*}\approx 0.9982\,, \quad \mathsf{k}_{*}\approx 0.7946\,. $$

(88)

Using (77), in our asymptotic analysis the optimal wave number as well as the bifurcation time are hence given by

$$ \frac{t_{\mathrm{b}}}{t_{\mathrm {c}}}=\frac{1}{1-\epsilon \cdot \mathsf {t}_{*}} \approx 1+\epsilon \cdot \mathsf {t}_{*}\,,\quad k_{*}= \frac{\mathsf{k}_{*}}{\epsilon }. $$

(89)

In Fig. 13(a), we compare the $k$-dependence of the Rayleigh quotient at fixed time, obtained respectively by the semi-analytical approach (see Fig. 7) and the asymptotic solution (84). Although the approximate Rayleigh quotient is slightly larger than the exact value, their dependence with respect to $k$ is in perfect agreement. In fact the optimal wave number in this case is 11 using the exact approach, and approximately 11.3 with the asymptotic solution.

Fig. 13

Comparison between the semi-analytical (exact) bifurcation solutions and the asymptotic approach: (a) Rayleigh quotient $\lambda _{k}$ as a function of the wave number $k$ for $\ell /R=0.05$ at $t/t_{\mathrm {c}}\approx 1.073$; (b) time-dependence of the optimal Rayleigh quotient $\lambda _{*}$

The time-dependence of the optimal Rayleigh quotient $\lambda _{*}$, evaluated with the optimal wave number $k_{*}$, is presented in Fig. 13(b). The previous semi-analytical result in Fig. 8 and the asymptotic solution are compared. It can be seen that the approximation is better with smaller values $\epsilon$. Due to the universal nature, the implicit $\epsilon$-dependence of $\lambda _{*}$ is introduced by the rescaled time parameter $\mathsf{t}$ given by (47). Using the fact that $\mathsf{t}\mapsto \lambda _{*}$ is decreasing (see Fig. 12), we deduce immediately that $\lambda _{*}$ decreases when $\epsilon$ becomes smaller. This result is confirmed in Fig. 13(b).

Finally, in Fig. 14 we review the size effect computed by the semi-analytical approach and the asymptotic solution. The asymptotic solution (89) predicts relatively well the $\epsilon$-dependence of the bifurcation time and the optimal wave number.

Fig. 14

Size effect of bifurcation with the semi-analytical approach and the asymptotic solution: (a) bifurcation time $t_{*}/t_{\mathrm {c}}$; (b) optimal wave number $k_{*}$

5 Conclusion and Perspectives

In this work the elastic-gradient damage evolution problem of a cylinder under torsion is successfully analyzed using two approaches. In the first approach, the fundamental branch and the its subsequent bifurcation are solved using analytical and numerical methods, where the results obtained are valid for arbitrary values of the internal length. In the second asymptotic approach, we assume that the length scale $\epsilon =\ell /R$ between the material internal length $\ell$ and the cylinder radius $R$ is small. It is found that the simulation results obtained by the semi-analytical (or analytical-numerical) approach can be formally justified by the asymptotic methods.

One of the main contribution of this work is the application of such boundary layer method for the study of gradient-damage models. The compatibility between the rescaled spatial and temporal variables is formally proved in Proposition 1. The orders of magnitude of the bifurcated solutions with respect to the small parameter $\epsilon$ are also carefully analyzed in Proposition 2. It is shown that the axisymmetric damage evolution and the bifurcation are governed by two universal functions independent of the small parameter. The $\epsilon$-dependence of the solutions can be explained largely by the introduced spatial and temporal rescaling.

• 1. The first universal function as illustrated in Fig. 10 governs the axisymmetric damage, and in particular its thickness evolution.

• 2. The second as shown in Fig. 12 gives a universal temporal evolution of the optimal Rayleigh quotient, which governs bifurcation from the fundamental branch.

The size effects of bifurcation formally derived in (89) and illustrated in Fig. 14 constitute the main results of this paper. Similar to the unidimensional problem as well as the 2d thermal shock problem, bifurcation is more likely to produce earlier for smaller values of the internal length.

In this paper, we focused on the loss of uniqueness of the fundamental branch characterized by the asymmetric damage solution. However, a more complete analysis should also involve a stability study of the bifurcated solutions. Furthermore, subsequent bifurcations may produce since it is not clear that the bifurcated damage pattern as presented in Fig. 7(b) may eventually evolve smoothly into fully-established cracks. Our numerical simulations not reported in this paper actually suggest that the bifurcated solution analyzed in this paper is stable for a finite time, see Fig. 15(a), during which the damage field is indeed periodic and agrees well with our semi-analytical and asymptotic analyses. However afterwards a second bifurcation, more abrupt than the previous one, takes place and leads to the final fracture of the cylinder, see Fig. 15(b). The numerical results will be reported in another paper in which this second bifurcation will be analyzed.

Fig. 15

(a) Bifurcated damage solution for $t_{\mathrm{b}}< t< t_{\mathrm{r}}$; (b) final fracture pattern at $t_{\mathrm{r}}$ for $\ell /R=0.05$

The current study is carried out using a particular set of damage constitutive functions (14). This is in general a preferred choice compared to other constitutive laws in which the elastic domain is absent. Future work could be devoted to other strongly-brittle gradient-damage materials since bifurcation behaviors could be different.

The bifurcation analysis and the boundary layer method could also be applied for three-dimensional gradient-damage problems. The physical role played by the internal length as well as the size-effects in damage evolution can thus be investigated analytically beyond the usual uni- or two-dimensional settings. As mentioned in the introduction, mixed mode I and III loading can also be considered in the future. We may hope that the experimentally observed echelon cracks may correspond in fact to a bifurcation mode similar to that observed in Fig. 7(b).

Appendix. Numerical Minimization of the Rayleigh Quotient

The generalized symmetric eigenvalue problem defined by (44) and the subsequent minimization problem of the Rayleigh quotient (42) are solved numerically. Standard $\mathbb{P}_{1}$ finite elements are used to discretize the functions $(A,C)$ in the interval $[0,R]$. After discretization the eigenvalue problem (44) becomes

$$ \boldsymbol {K}_{k}\boldsymbol {x}_{k}=\lambda _{k}\boldsymbol {M}\boldsymbol {x}_{k}\,, $$

(90)

where

• The matrices $\boldsymbol {K}_{k}$ and $\boldsymbol {M}$ correspond to the discrete quadratic forms $\mathsf{A}$ and $\mathsf{B}$;

• The eigenvector $\boldsymbol {x}_{k}\neq \boldsymbol {0}$ regroups the nodal values of the functions $(A_{k},C_{k})$;

• The smallest eigenvalue $\lambda _{k}$ is a finite-element approximation of the continuous one.

In this paper spatial discretization is performed with the FEniCS framework [19]. A specific conjugate gradient procedure described in [14] implemented in the library SLEPc [33] is applied to solve the discrete eigenvalue problem (90).

The subsequent minimization problem (45) with respect to the wave number $k$ is performed through direct evaluations of the Rayleigh quotient $\lambda _{k}$ for $k\in \mathbb{K}$ where $\mathbb{K}$ is a subset of $\mathbb{N}^{*}$ which is supposed to contain the minimum wave number. The minimization procedure of the Rayleigh quotient is summarized in Algorithm 1.

Algorithm 1

Minimizing the Rayleigh quotient (42) at a given instant $t>t_{\mathrm {c}}$

The next objective would be to find the bifurcation time $t_{*}$ at which the optimal Rayleigh quotient reaches 1. Remark that the above Algorithm 1 materializes a scalar function $t\mapsto \lambda _{*}$ defined for $t>t_{\mathrm {c}}$. A classical root-finding method is thus applied to find the corresponding instant $t_{*}$ when $\lambda _{*}=1$.