Abstract
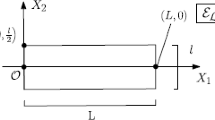
Simple extension and contraction of incompressible non-linearly elastic materials is considered here, with cuboid specimens stretched or contracted in one of the principal directions. Although the average stretch of infinitesimal line elements in such deformations is always extensile, the local response is much more nuanced. We examine the variation of the squared stretch with applied stretch and line element orientation in the undeformed configuration. The response of interest here is the percentage of directions at a point for which the material is in compression which we call the amount of material in compression. It is shown that the maximum amount of compression attainable is approximately \(61\%\) which occurs for infinitesimal contractions. Further contraction results in a decrease in the amount of material in compression, with the material being extensile almost everywhere in the limit of zero axial stretch. On the other hand, for simple extension, the amount of material in compression is a monotonically decreasing function of axial stretch, with \(39\%\) in compression for infinitesimal strains. The amount of material in compression therefore exhibits a discontinuity in the reference configuration. The amount of material in compression is still significant for moderate extensions, with, for example, \(25\%\) of the material still in compression for \(100\%\) stretch. Suspecting that this somewhat surprising response is a result of assuming perfect incompressibility, the effect of compressibility on the amount of material in compression is examined within the context of the linear theory for isotropic elastic materials.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Truesdell, C., Noll, W.: The Non-linear Field Theories of Mechanics. Springer, Berlin (2004)
Atkin, R.J., Fox, N.: An Introduction to the Theory of Elasticity. Longman, London (1980)
Ogden, R.W.: Non-linear Elastic Deformations. Dover, New York (1984)
Treloar, L.R.G.: The Physics of Rubber Elasticity. Oxford University Press, London (1975)
Horgan, C.O., Murphy, J.G.: Magic angles for fibrous incompressible elastic materials. Proc. R. Soc. A 474, 20170728 (2018)
Murphy, J.G.: Transversely isotropic biological soft tissue must be modeled using both anisotropic invariants. Eur. J. Mech. A, Solids 42, 90–96 (2013)
Horgan, C.O., Murphy, J.G.: The counterintuitive out-of-plane strength of incompressible orthotropic hyperelastic materials. Int. J. Solids Struct. 115, 170–179 (2017)
De Rosa, E., Latorre, M., Montans, F.J.: Capturing anisotropic constitutive models with WYPiWYG hyperelasticity; and on consistency with the infinitesimal theory at all deformation levels. Int. J. Non-Linear Mech. 96, 75–92 (2017)
Horgan, C.O., Murphy, J.G.: Magic angles and fibre stretch in arterial tissue: insights from the linear theory. J. Mech. Behav. Biomed. Mater. 88, 470–477 (2018)
Goriely, A., Tabor, M.: Rotation, inversion and perversion in anisotropic elastic cylindrical tubes and membranes. Proc. R. Soc. A 469, 20130011 (2013)
Demirkoparan, H., Pence, T.J.: Magic angles for fiber reinforcement in rubber-elastic tubes subject to pressure and swelling. Int. J. Non-Linear Mech. 68, 87–95 (2015)
Goriely, A.: The Mathematics and Mechanics of Biological Growth. Springer, New York (2017)
Horgan, C.O., Murphy, J.G.: Magic angles in the mechanics of fibrous soft materials. Mech. Soft Mater. 1, 1–6 (2019)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Horgan, C.O., Murphy, J.G. The Unexpected Kinematics of Simple Extension and Contraction of Incompressible Materials. J Elast 138, 195–203 (2020). https://doi.org/10.1007/s10659-019-09737-9
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-019-09737-9