Finite Anticlastic Bending of Hyperelastic Solids and Beams

Abstract

This paper deals with the equilibrium problem in nonlinear elasticity of hyperelastic solids under anticlastic bending. A three-dimensional kinematic model, where the longitudinal bending is accompanied by the transversal deformation of cross sections, is formulated. Following a semi-inverse approach, the displacement field prescribed by the above kinematic model contains three unknown parameters. A Lagrangian analysis is performed and the compressible Mooney-Rivlin law is assumed for the stored energy function. Once evaluated the Piola-Kirchhoff stresses, the free parameters of the kinematic model are determined by using the equilibrium equations and the boundary conditions. An Eulerian analysis is then accomplished to evaluating stretches and stresses in the deformed configuration. Cauchy stress distributions are investigated and it is shown how, for wide ranges of constitutive parameters, the obtained solution is quite accurate. The whole formulation proposed for the finite anticlastic bending of hyperelastic solids is linearized by introducing the hypothesis of smallness of the displacement and strain fields. With this linearization procedure, the classical solution for the infinitesimal bending of beams is fully recovered.

1 Introduction

The flexure of an elastic body is a classical problem of elastostatics that has been widely investigated in literature because of its great relevance in many practical tasks. The majority of studies has been performed by assuming infinitesimal strains and small displacements of the body under bending (see, among the others, Bernoulli Jacob [1], Bernoulli Jacques [2], Parent [3], Euler [4–7], Navier [8], Barré de Saint Venant [9], Bresse [10], Lamb [11], Kelvin and Tait [12] and Love [13]).

One of the first investigations dealing with the above equilibrium problem in the framework of finite elasticity was carried out by Seth [14], who studied a plate under flexure in the absence of body forces. Based on the semi-inverse method, he assumed the deformed configuration of the plate like a circular cylindrical shell, keeping valid the Bernoulli-Navier hypothesis for cross sections and assuming a linear dependence for the displacement field. Moreover, he assumed that the stress depends on the strain according to the linearized theory of elasticity. In his work, the bending couples needed to induce the hypothesized configuration of the plate together with the position of the unstretched fibers within the plate thickness (neutral axis) were also assessed.

The flexion problem of an elastic block has been studied by Rivlin [15], considering the deformation that transforms the elastic block into a cylinder having the base in the shape of a circular crown sector. No displacements along the axis of the cylinder have been taken into account, making the problem as a matter of fact two-dimensional. Surface tractions necessary to induced the assumed displacement field have been determined, showing that in the case of an incompressible neo-Hookean material, these surface tractions are equivalent to two equal and opposite couples acting at the end faces. Subsequently, Rivlin generalized his study formulating the equilibrium problem without specifying the form of the stored energy function [16].

Shield [17] investigated the problem of a beam under pure bending by assuming small strain but large displacements. He retrieves the Lamb’s solution [11] for the deflection of the middle surface of the beam. As remarked in that work, for large values of the width-to-thickness ratios, the deflection profile is flat in the central portion of the cross section and oscillatory near the edges.

A closed-form solution of a compressible rectangular body made of Hencky material under finite plane bending has been obtained by Bruhns et al. [18], giving explicit relationships for the bending angle and bending moment as functions of the circumferential stretch.

It is important to note that all the aforementioned works address the bending problem in a two-dimensional context, neglecting systematically the deformation in the direction perpendicular to the inflexion plane. Proceeding in this way, the modeling is simplified substantially, since the displacement field is assumed to be plane, renouncing to describe a phenomenon which in reality is purely three-dimensional. In particular, the transversal deformation, always coupled with the longitudinal inflexion of a solid, is known as the anticlastic effect.

This paper presents a fully nonlinear analysis of solids under anticlastic bending. In the next section, a three-dimensional kinematic model, where the longitudinal bending is accompanied by the transversal deformation of cross sections, is formulated by introducing three basic hypotheses. Following a semi-inverse approach, the displacement field prescribed by the kinematic model contains three unknown parameters. In Sect. 3, a Lagrangian analysis is performed and the compressible Mooney-Rivlin law is assumed for the stored energy function. Once evaluated the Piola-Kirchhoff stresses, the free parameters of the kinematic model are determined by using the equilibrium equations and the boundary conditions. With the purpose of evaluating stretches and stresses in the deformed configuration, an Eulerian analysis is accomplished in Sect. 4. Cauchy stress distributions are investigated and intervals for the constitutive parameters, in which the solution is particularly accurate, are established. The whole formulation proposed for the finite anticlastic bending of hyperelastic solids is linearized in Sect. 5, by introducing the hypothesis of smallness of the displacement and strain fields. With this linearization procedure, the classical solution for the infinitesimal bending of beams is fully recovered.

2 Kinematics

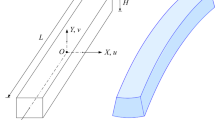
Let us consider a hyperelastic body composed of a homogeneous, isotropic and compressible material, having the shape of a rectangular parallelepiped. No requirement of slenderness (such as that usually postulated in technical theories of beams) is introduced. Reference is made to a Cartesian coordinate system $\{ O, X, Y, Z \}$ having the origin $O$ placed in the centroid of the body, as shown in Fig. 1a. Thus, the body can be identified with the closure of the following regular region:

$$ \mathcal{B}= \biggl\{ ( X, Y, Z ) \ \big| \ -\frac{B}{2}< X< \frac{B}{2}, -\frac{H}{2}< Y< \frac{H}{2}, - \frac{L}{2}< Z< \frac{L}{2} \biggr\} $$

of the three-dimensional Euclidean space ℰ. $B$, $H$ and $L$ respectively denote the width, height and length of the body. Although the formulation will be developed for a solid with a rectangular cross section, it can be readily extended to solids with a generic cross section provided that the symmetry with respect to the $Y$ axis is maintained.

Fig. 1

Prismatic solid $\bar{\mathcal{B}}$. (a) Undeformed configuration. (b) Deformed configuration

The undeformed configuration $\bar{\mathcal{B}}$ of the body is assumed as the reference configuration, whereas the deformed configuration is given by the deformation $\mathbf{f} : \bar{\mathcal{B}}\rightarrow \mathcal{V}$,¹ that is a smooth enough, injective and orientation-preserving (in the sense that $\det \mathbf{Df}>0$) vector field. The deformation of a generic material point $P$ can be expressed by the well-known relationship

$$ \mathbf{f}(P)=\mathbf{s}(P)+\mathbf{id}(P), $$

(1)

where $\mathbf{id}(P)$ and

$$ \mathbf{s}(P)=u(P) \mathbf{i}+ \mathit{v}(P)\mathbf{j}+w(P) \mathbf{k} $$

(2)

are the position and displacement vectors of the point $P$. Into (2), the functions $u(P)$, $v(P)$ and $w(P)$ are the scalar components of $\mathbf{s}(P)$, whereas $\mathbf{i}$, $\mathbf{j}$ and $\mathbf{k}$ are the unit vectors. The application of the material gradient operator $\mathbf{D}(\cdot )$ to (1) gives

$$ \mathbf{F}=\mathbf{H}+\mathbf{I}, $$

(3)

where $\mathbf{F}: \bar{\mathcal{B}}\rightarrow \mathit{Lin}^{+}$ and $\mathbf{H}: \bar{\mathcal{B}}\rightarrow \mathit{Lin}$ are the deformation and displacement gradients, respectively.² $\mathbf{I}$ is the identity tensor.

Fixed notation, hereinafter the formulation of the equilibrium problem of an inflexed solid will be performed. Solving such a problem means getting the displacement field. But, in general, this direct computation is a daunting task. Thus, to simplify the problem, some hypotheses, more or less based on the physical behavior of the solid, are generally postulated in the literature. In this work, the three-dimensionality of the problem is maintained, without renouncing to study none of the three components of the displacement field.³ This allows to examine, in addition to the longitudinal inflexion along the $Z$ axis of the solid, also the deformation of cross sections, which are initially parallel to the $XY$ plane. As show experimental evidences (see, e.g., [19] and [20]) the solid transversely undergoes a second inflexion, whose sign is opposite to that longitudinal, known as anticlastic effect. Although the longitudinal curvature is generally larger, the two curvatures may have comparable magnitudes.

Taking into account the above considerations, the displacement field will be partially defined by adopting a semi-inverse approach. To this aim, the following three basic hypotheses are introduced.

1. The solid is inflexed longitudinally with constant curvature. Namely, each rectilinear segment of the solid, parallel to the $Z$ axis, is transformed into an arc of circumference.

2. Plane cross sections, orthogonal to the $Z$ axis, remain as such after the solid has been inflexed. Cross sections can deform only in their own plane and all in the same way.

3. As a result of longitudinal inflexion, the solid is inflexed also transversally with constant curvature, in such a way that any horizontal plane of the solid is transformed into a toroidal open surface.

The longitudinal inflexion can be thought of as generated by the application of a pair of self-balanced bending moments or by a geometric boundary condition which imposes a prescribed relative rotation between the two end faces of the solid.

In this paper, on the basis of the three previous assumptions, a kinematic model containing some unknown deformation parameters is derived. The model describes the displacement field (2) of the solid and it is the outcome of coupled effects generated by the longitudinal and transversal curvatures. Through this kinematic model and relationship (1), the shape assumed by the solid in the deformed configuration is obtained (cf. Fig. 1b).

Points belonging to the deformed configuration are indicated with an apex, $(\cdot )'$. Components $u$, $v$ and $w$ are referred to the reference system $\{ O, X, Y, Z \}$ and for simplicity we begin to formulate our model by considering the displacement field of points belonging to the plane of symmetry $YZ$ (cf. Fig. 2).

Fig. 2

Deformation of the solid in the vertical $YZ$ plane

Figure 1b shows that material fibers at the top edge of the solid are elongated in the $Z$ direction (the corresponding longitudinal stretch $\lambda_{Z}$ will therefore be greater than one), while material fibers are shortened at the bottom edge ($\lambda_{Z}<1$). Accordingly, in the vertical $YZ$ plane, an intermediate curve, where there is no longitudinal deformation ($\lambda_{Z}=1$) exists. In Fig. 2 this special curve is represented by the circumferential arc drawn with a dotted line.⁴ On the other hand, fibers at the top edge of the solid are shortened in the $X$ and $Y$ directions, while they are elongated at the bottom edge (cf. Fig. 1b). This is the anticlastic effect associated with the inflexion of the solid in the $Z$ direction. In particular, in the generic cross section there will be a smooth curve with $\lambda_{Y}=1$. In the vertical $YZ$ plane, each of these curves has a point of intersection. Since cross sections are deformed all in the same way, these points longitudinally form the arc shown in Fig. 2. Points of this arc are images of points belonging to the horizontal rectilinear segment traced for the point $A$ of the undeformed configuration (cf. Fig. 2). The point $A$ is fixed, $A=A'$. The two longitudinal arcs, for which $\lambda_{Y}=1$ and $\lambda_{Z}=1$, are distinct. Furthermore, there is no a correlation between the points of these curves and the centroids of the deformed cross sections. These two arcs are crucial to describe the displacement field. The radius $R_{0}$ of the arc with $\lambda _{Z}=1$ is known, because it can be determined by using the geometric boundary condition which prescribes the angle $\alpha_{0}$, $R_{0}=L/2\alpha_{0}$.⁵ The radius $R$ of the arc with $\lambda_{Y}=1$ is instead unknown and its determination depends on resolving the equilibrium problem.

In the vertical $YZ$ plane, the generic point $P_{0} = (0, Y, Z)$ as a result of the deformation moves in $P_{0}'$ (cf. Fig. 2). This displacement is generated by a rigid translation, a rigid rotation and a pure deformation. The point $P_{0}$ belongs to the transversal $XY$ plane localized by variable $Z$. After deformation, this generic transversal plane for the hypothesis 2 is transformed into the plane identified by the angle $\alpha$ (cf. Fig. 2). The displacement of point $P_{0}$ is illustrated in Fig. 3. Figure 3a shows the displacement components $v_{1}$ and $w_{1}$ arising from the rigid translation of $Z$ cross section that shifts the point $P_{0}$ in $P_{1}$. These displacements components can be evaluated by observing that they coincide with those that transfer the point $N$ (belonging to the horizontal straight line $Y=-OA$) in its final position $N'$ (on the arc $\lambda_{Y}=1$) according to

$$ -v_{1}=R (1-\cos \alpha ), \quad \quad -w_{1}=Z-R \sin \alpha . $$

(4)

Due to the pure deformation along $Y$, the points that are positioned above $N'$, along the trace of the shifted cross section, undergo a contraction, while those below exhibit a dilation. These length variations are measured by the stretch $\lambda_{Y}$. The point $P_{1}$ thus moves to $P_{2}$ with the following vertical displacement (Fig. 3b):

$$ -v_{2}=P_{1}P_{2}=P_{0}N-P_{2}N'=Y+QN-P'_{0}N', $$

(5)

being

$$ P_{0}N=P_{1}N', \quad \quad P_{2}N'=P'_{0}N', \quad \quad P'_{0}N'= \int_{N}^{P_{0}} \lambda_{Y}(\hat{Y}) d \hat{Y}. $$

(6)

The rigid rotation of the cross section brings the point $P_{2}$ in $P'_{0}$ through the following displacement components (cf. Fig. 3b):

$$ -v_{3}=P'_{0}N' (1-\cos \alpha ), \quad \quad w_{3}=P'_{0}N' \sin \alpha , $$

(7)

where the point $N'$ acts as rotation center and the rotation angle $\alpha$ is amounting to $Z/R_{0}$. By summing the three contributions (4), (5) and (7), the displacement components $v$ and $w$ illustrated in Fig. 2, which transfer the point $P_{0}=(0, Y, Z)$ in $P'_{0}=(0, Y+v, Z+w)$, are evaluated

$$ \textstyle\begin{cases} v=-R (1-\cos \alpha )-Y-QN+P'_{0}N' \cos \alpha \\ w=-Z+R \sin \alpha +P'_{0}N' \sin \alpha . \end{cases} $$

(8)

These displacement components are due only to the longitudinal curvature of the solid. Now we turn to examine the displacement field in the transversal cross section $\varOmega$, inclined by the angle $\alpha$, as shown in Fig. 4. Even here it is essential to identify the curve that in the $X$ direction does not change its length. Points that are located above this curve suffer contractions in the $X$ and $\tilde{Y}$ directions, those below are elongated along the same directions. As shown by Fig. 4, the curve with $\lambda_{X}=1$ is an arc, whose radius is denoted by $r$. The radius $r$ is an unknown kinematic parameter, which, for the hypothesis 2, assumes the same value for all cross sections variously inclined. This parameter measures the anticlastic effect. Let us consider the point $P_{4}$, such that $P'_{0}N'=P_{4}N_{1}$, positioned to the generic $X$ distance from the point $N'$. Owing to the anticlastic curvature, the point $P_{4}$ goes in the position $P'$. This last transformation can be decomposed into a rigid translation that moves $P_{4}$ in $P_{5}$ and $N_{1}$ in $N_{2}$ (cf. Fig. 5)

$$ -u_{4}=X-r \sin \beta , \quad \quad \tilde{v}_{4}=r (1- \cos \beta ), $$

(9)

where $\beta =X/r$, and into a subsequent rotation, with center in $N_{2}$ and angle $\beta$, that brings $P_{5}$ in the final position $P'$ (cf. Fig. 5)

$$ -u_{5}=P'_{0}N' \sin \beta , \quad \quad -\tilde{v}_{5}=P'_{0}N' (1-\cos \beta ). $$

(10)

Therefore, in the cross section $\varOmega$, the following components are obtained:

$$ u=-X+r \cos \beta -P'_{0}N' \sin \beta , \quad \tilde{v}=r (1- \cos \beta )-P'_{0}N' (1-\cos \beta ). $$

(11)

The component $\tilde{v}$ can then be decomposed with respect to the reference system, as indicated in Fig. 5, obtaining

$$ \textstyle\begin{cases} u=-X+(r-P'_{0}N') \sin \beta \\ v=(r-P'_{0}N') (1-\cos \beta ) \cos \alpha \\ w=(r-P'_{0}N') (1-\cos \beta ) \sin \alpha . \end{cases} $$

(12)

These displacements components are due to the transversal curvature of the cross sections and are measured starting from the cylindrical configuration of the solid only longitudinally inflexed. Such a configuration can be described by means of (8) with the addition of $u=0$. Adding up (8) and (12), the displacement field, which carries the generic material point $P=(X, Y, Z)$ in its final position $P'=(X+u, Y+v, Z+w)$ in the deformed configuration of the solid, is achieved

$$ \textstyle\begin{cases} u=-X+(r-P'_{0}N') \sin \frac{X}{r} \\ v=-R (1-\cos \frac{Z}{R_{0}})-Y-QN+P'_{0}N' \cos \frac{Z}{R_{0}}+(r-P'_{0}N') (1-\cos \frac{X}{r}) \cos \frac{Z}{R_{0}} \\ w=-Z+(R+P'_{0}N') \sin \frac{Z}{R_{0}}+(r-P'_{0}N') (1-\cos \frac{X}{r}) \sin \frac{Z}{R_{0}}. \end{cases} $$

(13)

Fig. 3

Composition of the displacement field in the vertical $YZ$ plane for the generic cross section. (a) Rigid translation. (b) Pure deformation and rigid rotation

Fig. 4

Deformation of the generic cross section $\varOmega$

Fig. 5

Composition of the displacement field in the generic cross section $\varOmega$

In the above displacement field, an expression can be attributed to the segment $P'_{0}N'$. To assess the integral expression of $P'_{0}N'= \int_{N}^{P_{0}}\lambda_{Y}(\hat{Y}) d\hat{Y}$, the following relationship due to the isotropy property⁶ of the solid can be used:

$$ \lambda_{X}=\lambda_{Y}. $$

(14)

In order to evaluated these stretches it is useful to recall the definition of right Cauchy-Green strain tensor $\mathbf{C}$ and of left Cauchy-Green strain tensor $\mathbf{B}$

$$ \mathbf{C}=\mathbf{F}^{T}\mathbf{F}=\mathbf{U} \mathbf{R}^{-1} \mathbf{RU}=\mathbf{U}^{2}, \qquad \mathbf{B}= \mathbf{F} \mathbf{F}^{T}=\mathbf{R} \mathbf{UUR}^{-1}= \mathbf{RU}^{2}\mathbf{R}^{-1}, $$

(15)

where the two tensors R and U are obtained by the polar decomposition of the deformation gradient $\mathbf{F}= \mathbf{RU}$. R is a proper orthogonal tensor and denotes the rotation tensor, whereas U is a symmetric and positive definite tensor that indicates the right stretch tensor. For the state of deformation derived from (13), tensor U is diagonal, because the reference system $\{ O, X, Y, Z \}$ is principal. Diagonal components of U are the principal stretches. Therefore, the diagonal components of C are⁷

$$ \begin{aligned} &C_{11}=F_{11}^{2}+F_{21}^{2}+F_{31}^{2}= \lambda_{X}^{2}, \\ & C_{22}=F_{12}^{2}+F_{22}^{2}+F_{32}^{2}= \lambda_{Y}^{2}, \\ & C_{33}=F_{13}^{2}+F_{23}^{2}+F_{33}^{2}= \lambda_{Z}^{2}. \end{aligned} $$

(16)

Using (3) and computing the derivatives of the displacement field (13), equations (16) provide the following expressions for the stretches:

$$ \textstyle\begin{cases} \lambda_{X}=\frac{r-P'_{0}N'}{r} \\ \lambda_{Y}=\frac{\partial P'_{0}N'}{\partial Y} \\ \lambda_{Z}=\frac{R}{R_{0}}+\frac{P'_{0}N'}{R_{0}}+\frac{(r-P'_{0}N') (1-\cos \beta ) }{R_{0}}, \end{cases} $$

(17)

taking into account that stretches are strictly positive quantities. The condition (14) can now be set by equating the first two expressions of (17). In this way, the following differential equation is derived:

$$ r \frac{\partial (P'_{0}N')}{\partial Y}+P'_{0}N'-r=0, $$

(18)

whose solution is

$$ P'_{0}N'=r-e^{-\frac{1}{r}(Y+QN)-C_{1}}. $$

(19)

The integration constant $C_{1}$ can be determined by imposing the condition

$$ \lambda_{Y}(-QN)=\frac{\partial (P'_{0}N')}{\partial Y}\bigg|_{Y=-QN} =1, $$

(20)

that gives $e^{-C_{1}}=r$. Thus

$$ P'_{0}N'=r \bigl(1-e^{-\frac{1}{r}(Y+QN)} \bigr). $$

(21)

With this expression for $P'_{0}N'$, stretches (17) transform into

$$ \textstyle\begin{cases} \lambda_{X}=\lambda_{Y}=e^{-\frac{1}{r}(Y+QN)} \\ \lambda_{Z}=\frac{R+r-r e^{-\frac{1}{r}(Y+QN)}\cos \frac{X}{r}}{R _{0}}. \end{cases} $$

(22)

Although the displacement field (13) is quite complicated, the transversal stretches, $\lambda_{X}$ and $\lambda_{Y}$, are expressed by means of a very simple exponential function. It is immediate to verify that, for $Y=-QN$, $\lambda_{X}= \lambda_{Y}=1$. In addition, $\lambda_{X}$ and $\lambda_{Y}$ are lower than one (i.e., transversal fibers are shortened) for $Y>-QN$. Vice versa, they are greater than one (i.e., transversal fibers are elongated) for $Y<-QN$. This coherently with the kinematic model shown in Fig. 2 and Fig. 4. The expression of the longitudinal stretch $\lambda_{Z}$ has a slightly more complex form, due to the further dependence on the variable $X$. In fact, the transversal curvature, in the inclined plane $\varOmega$, produces a further contribution to the length variation of fibers in the $Z$ direction. In the vertical plane of symmetry, $X = 0$, this stretch is equal to one in correspondence of the particular value $Y_{M}$, ordinate of point $M$ in the undeformed configuration, for which it is $P'_{0}N'=M'A'=R_{0}-R$, namely⁸

$$ Y_{M}=-r \ln \biggl( \frac{R+r-R_{0}}{r} \biggr) -QN. $$

(23)

For $Y>Y_{M}$ the longitudinal fibers are elongated, while for $Y< Y_{M}$ they are shortened (cf. Fig. 2). Always in the same plane, $\lambda_{Z}=\frac{R+P'_{0}N'}{R_{0}}$. In particular, $\lambda_{Z}=\frac{R+r-r e^{-\frac{QN}{r}}}{R_{0}}$ for $Y=0$ and $\lambda_{Z}=\frac{R}{R _{0}}$ for $Y=-QN$. Moreover, $\lambda_{Y}=\frac{R+r-R_{0}}{r}$ for $Y=Y_{M}$. Diagrams of stretches minus one for the vertical line with $X = Z = 0$ are shown in Fig. 6. These diagrams, obtained by using (22), allow to readily view the portions of the cross section that are elongated (positive values) and those which are shortened (negative values). Inside the cross section, the plot of $\lambda_{Y}$ is the same for all $X\in [ -\frac{B}{2}, \frac{B}{2} ]$, while that of $\lambda_{Z}$ varies for the presence of the term $\cos \frac{X}{r}$. This scenario regarding to the cross section $Z=0$ repeats equal to itself for all cross sections of the solid, namely for all $Z\in [- \frac{L}{2}, \frac{L}{2}]$. From Fig. 6 it can be observed that the two functions ($\lambda_{Z}-1$) and ($\lambda_{Y}-1$) have the opposite sign at the upper and lower fibers, so as to generate the anticlastic effect. While they have the same sign in the central portion $MA$.

Fig. 6

Plot of stretches $\lambda_{Z}$ and $\lambda_{X}=\lambda _{Y}$ for $X=Z=0$

Substituting (21) into (13), the definitive displacement field is obtained

$$ \textstyle\begin{cases} u=-X+r e^{-\frac{1}{r}(Y+QN)} \sin \frac{X}{r} \\ v=-Y-R-QN+ [ R+r-r e^{-\frac{1}{r}(Y+QN)}\cos \frac{X}{r} ] \cos \frac{Z}{R_{0}} \\ w=-Z+ [ R+r-r e^{-\frac{1}{r}(Y+QN)}\cos \frac{X}{r} ] \sin \frac{Z}{R_{0}}. \end{cases} $$

(24)

This system has three unknown kinematic parameters: $QN$, $R$ and $r$. By applying the material gradient to (24) and using (3), components of the deformation gradient F are calculated

$$ [ \mathbf{F} ] =\left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \lambda_{X}\cos \beta & -\lambda_{Y}\sin \beta & 0 \\ \lambda_{X}\sin \beta \cos \alpha & \lambda_{Y}\cos \beta \cos \alpha & -\lambda_{Z}\sin \alpha \\ \lambda_{X}\sin \beta \sin \alpha & \lambda_{Y}\cos \beta \sin \alpha & \lambda_{Z}\cos \alpha \end{array}\displaystyle \right ] . $$

(25)

Given the polar decomposition theorem, it is immediate to write the deformation gradient (25) as product of the rotation tensor by the stretch tensor

$$\begin{aligned} & [ \mathbf{R} ] =\left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \cos \beta & -\sin \beta & 0 \\ \sin \beta \cos \alpha & \cos \beta \cos \alpha & -\sin \alpha \\ \sin \beta \sin \alpha & \cos \beta \sin \alpha & \cos \alpha \end{array}\displaystyle \right ] , \end{aligned}$$

(26)

$$\begin{aligned} &[ \mathbf{U} ] =\left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \lambda_{X} & 0 & 0 \\ 0 & \lambda_{Y} & 0 \\ 0 & 0 & \lambda_{Z} \end{array}\displaystyle \right ] . \end{aligned}$$

(27)

3 Lagrangian Analysis

Constitutive properties of a hyperelastic material are described by the stored energy function $\omega$

$$ \mathbf{T}_{R}=\frac{\partial \omega }{\partial \mathbf{F}}, $$

(28)

where $\mathbf{T}_{R}$ is the (first) Piola-Kirchhoff stress tensor. If the material is homogeneous and isotropic, and if the function $\omega$ is frame-indifferent, then, it depends only on the principal invariants of $\mathbf{B}$ or equivalently of $\mathbf{C}$

$$ \omega =\hat{\omega } ( I_{1}, I_{2}, I_{3} ) , $$

(29)

where⁹

$$\begin{aligned} &I_{1}=\| \mathbf{F}\|^{2}= \lambda_{X}^{2}+\lambda_{Y} ^{2}+ \lambda_{Z}^{2}, \\ & I_{2}=\| \mathbf{F}^{\star }\|^{2}= \lambda_{X}^{2} \lambda_{Y}^{2}+ \lambda_{X}^{2}\lambda_{Z}^{2}+ \lambda_{Y}^{2}\lambda _{Z}^{2}, \\ & I_{3}=(\det \mathbf{F})^{2}=\lambda_{X}^{2} \lambda_{Y}^{2}\lambda _{Z}^{2}. \end{aligned}$$

Substituting the derivative of $\omega$ with respect to the deformation gradient into (28), the constitutive law is derived

$$ \mathbf{T}_{R}=2 \biggl( \frac{\partial \omega }{\partial I_{1}}+I_{1} \frac{ \partial \omega }{\partial I_{2}} \biggr) \mathbf{F}-2\frac{\partial \omega }{\partial I_{2}}\mathbf{BF}+2I_{3} \frac{\partial \omega }{ \partial I_{3}}\mathbf{F}^{-T}. $$

(30)

Being $\mathbf{BF}=\mathbf{R}\mathbf{U}^{3}$ and $\mathbf{F}^{-T}=\mathbf{R}\mathbf{U}^{-1}$, this equation can be rewritten as

$$ \mathbf{T}_{R}=\mathbf{RS}, $$

(31)

where S is a diagonal tensor

$$ [ \mathbf{S} ] =\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} S_{X} & 0 & 0 \\ 0 & S_{Y} & 0 \\ 0 & 0 & S_{Z} \end{array}\displaystyle \right ] , $$

(32)

with

$$ S_{J}=2 \biggl( \frac{\partial \omega }{\partial I_{1}}+I_{1}\frac{ \partial \omega }{\partial I_{2}} \biggr) \lambda_{J}-2\frac{\partial \omega }{\partial I_{2}}\lambda_{J}^{3}+2I_{3} \frac{\partial \omega }{ \partial I_{3}}\frac{1}{\lambda_{J}},\quad \mbox{for}\ J=X, Y, Z. $$

(33)

Equilibrium requires that the following vectorial equation must be satisfied locally:

$$ \mathrm{Div} \mathbf{T}_{R}+\mathbf{b}=\mathbf{o}. $$

(34)

In the absence of body forces b and computing the scalar components of the material divergence of $\mathbf{T}_{R}$, a system of three partial differential equations is obtained

$$ \textstyle\begin{cases} -S_{X}\frac{1}{r}\sin \frac{X}{r}+S_{X,X}\cos \frac{X}{r}-S_{Y,Y} \sin \frac{X}{r}=0 \\ S_{X}\frac{1}{r}\cos \frac{X}{r}\cos \frac{Z}{R_{0}}+S_{X,X}\sin \frac{X}{r}\cos \frac{Z}{R_{0}}+S_{Y,Y}\cos \frac{X}{r}\cos \frac{Z}{R _{0}}-S_{Z}\frac{1}{R_{0}}\cos \frac{Z}{R_{0}}-S_{Z,Z}\sin \frac{Z}{R _{0}}\\\quad =0 \\ S_{X}\frac{1}{r}\cos \frac{X}{r}\sin \frac{Z}{R_{0}}+S_{X,X}\sin \frac{X}{r}\sin \frac{Z}{R_{0}}+S_{Y,Y}\cos \frac{X}{r}\sin \frac{Z}{R _{0}}-S_{Z}\frac{1}{R_{0}}\sin \frac{Z}{R_{0}}+S_{Z,Z}\cos \frac{Z}{R _{0}}\\\quad =0, \end{cases} $$

(35)

where $S_{J,J}=\frac{\partial S_{J}}{\partial J}$ for $J=X, Y, Z$ (no sum). These derivatives are computed in Appendix A. System (35), which governs locally equilibrium conditions, has a very complex form. But above all, it must be taken in mind that, having been hypothesized a priori the displacement field, it does not exist the actual possibility to exactly solve the system (35) for all internal points of the body.

Nevertheless, some information about the free parameters of the displacement field can be obtained by imposing the equilibrium in special points of the body. In particular, the longitudinal basic line, whose points have the following coordinates: $X=0, Y=-QN$ and $Z=Z$, shows a kinematics completely and properly described by the two radii $R$ and $r$. In the sense that these two parameters have been defined precisely for the longitudinal basic line and then, assumed as constant values by the kinematic model, they have also been employed to describe the kinematics of all other points of the solid. Therefore, as one moves away from the basic line, the values of $R$ and $r$ are becoming increasingly approximated. The longitudinal basic line is characterized by

$$ \lambda_{X}=\lambda_{Y}=1, \qquad \lambda_{Z}= \frac{R}{R_{0}}. $$

(36)

For it and taking into account quantities (79) reported in Appendix A, the system (35) specializes in

$$ \textstyle\begin{cases} S_{X,X}=0 \\ S_{X}\frac{1}{r}\cos \frac{Z}{R_{0}}+S_{Y,Y}\cos \frac{Z}{R_{0}}-S _{Z}\frac{1}{R_{0}}\cos \frac{Z}{R_{0}}=0 \\ S_{X}\frac{1}{r}\sin \frac{Z}{R_{0}}+S_{Y,Y}\sin \frac{Z}{R_{0}}-S _{Z}\frac{1}{R_{0}}\sin \frac{Z}{R_{0}}=0, \end{cases} $$

(37)

and, since the two trigonometric functions $\sin \frac{Z}{R_{0}}$ and $\cos \frac{Z}{R_{0}}$ are never simultaneously zero, this system reduces to

$$ \textstyle\begin{cases} S_{X,X}=0 \\ S_{X}\frac{1}{r}+S_{Y,Y}-S_{Z}\frac{1}{R_{0}}=0. \end{cases} $$

(38)

To proceed it should now be assigned a specific law to the stored energy function $\omega$. For it the compressible Mooney-Rivlin form is assumed:¹⁰

$$ \omega (I_{1}, I_{2}, I_{3})=a I_{1}+b I_{2}+c I_{3}-\frac{d}{2} \ln I_{3}, $$

(39)

where the constants $a$, $b$, $c$ and $d$ are strictly positive quantities. Is well known that the above stored energy function describes properly the constitutive behavior of rubbers and rubber-like materials. Through (39), the following set of derivatives is computed:

$$ \begin{aligned} &\omega_{1}=a,\qquad \omega_{1,X}=\omega_{1,Y}=0, \\ &\omega_{2}=b,\qquad \omega_{2,X}=\omega_{2,Y}=0, \\ &\omega_{3}=c-\frac{d}{2I_{3}},\qquad \omega_{3,X}= \frac{d}{R_{0}} \frac{1}{ \lambda_{Z}^{3}} e^{\frac{3}{r}(Y+QN)} \sin \frac{X}{r}, \\ &\omega_{3,Y}=-\frac{d}{2} e^{\frac{4}{r}(Y+QN)} \biggl( \frac{4}{r} \frac{1}{ \lambda_{Z}^{2}}-\frac{2}{R_{0}} \frac{1}{\lambda_{Z}^{3}} e^{- \frac{1}{r}(Y+QN)}\cos \frac{X}{r} \biggr) . \end{aligned} $$

(40)

Among the four constants in (39), a relationship can be established by imposing that, in the absence of deformation, the stress vanishes. By setting $\alpha =\beta =0$ into (30), the stresses $T_{R,ij}$, with $i\neq j, \mbox{for}\ i, j=1,~2, 3$, are zero, whereas the diagonal components for $\lambda_{J}=1$ are

$$ T_{R,11}=T_{R,22}=T_{R,33}=2 ( \omega_{1}+2 \omega_{2}+\omega_{3} ) |_{\lambda_{J}=1}=0. $$

(41)

Using (40), this condition gives¹¹

$$ d=2 ( a+2 b+c ) . $$

(42)

Let us go back now to equilibrium equations (38) written for the longitudinal basic line. Taking into account the expression of $S_{X,X}$, provided by (79), and being $\omega_{1,X}= \omega_{2,X}=0$ for (40) and $\omega_{3,X}=0$ in correspondence of the basic line, the first equation of system (38), which governs the equilibrium along $X$, is identically satisfied,¹² since all its terms are null. With (36), (79) and (40), the following terms can be evaluated:

$$ \begin{aligned} & S_{X}=2a+2b \biggl[ 1+ \biggl( \frac{R}{R_{0}} \biggr) ^{2} \biggr] +2c \biggl( \frac{R}{R _{0}} \biggr) ^{2}-d, \\ & S_{Y,Y}=-\frac{2}{r} a+ \biggl[ -\frac{6}{r}+4 \frac{R}{R_{0}^{2}}- \frac{2}{r} \biggl( \frac{R}{R_{0}} \biggr) ^{2} \biggr] b+ \biggl[ 4 \frac{R}{R _{0}^{2}}-\frac{6}{r} \biggl( \frac{R}{R_{0}} \biggr) ^{2} \biggr] c- \frac{d}{r}, \\ & S_{Z}=2a \frac{R}{R_{0}}+4b \frac{R}{R_{0}}+2c \frac{R}{R_{0}}-d \frac{R _{0}}{R}. \end{aligned} $$

(43)

Substituting (42) and (43) in the second equation of system (38), which governs the equilibrium along $Y$ and $Z$, the following expression between the two kinematic unknown parameters $r$ and $R$ is derived:

$$ r \bigl[ a \bigl( R_{0}^{2}-R^{2} \bigr) +2bR_{0}^{2}+c \bigl( R_{0}^{2}+R ^{2} \bigr) \bigr] -2R \bigl[ aR_{0}^{2}+3bR_{0}^{2}+c \bigl( R_{0}^{2}+R ^{2} \bigr) \bigr] =0. $$

(44)

If relationship (44) is satisfied, all points of the longitudinal basic line are in equilibrium. Although in our model there are still two relationships among the free parameters to be determined, for all points of the basic line the displacement field is correct when (44) is satisfied, being it kinematically compatible and equilibrated.

When the basic line is abandoned, the equilibrium equations become much more complicated. Nevertheless, it is reasonable to expect, as a result of the continuity of the displacement field, that the above solution will be yet accurate in a neighborhood of each single point belonging to the basic line (to show this particular aspect of the problem, in the next section, a specific numerical analysis will be performed).

To complete the formulation of the boundary-value problem, the boundary conditions must be added to the field equations (35). Let us leave aside for now the boundary conditions on the two bases of the solid (i.e., for the two cross sections with $Z=-L/2$ and $Z=L/2$), which will be used to prescribe the angle $\alpha_{0}$. For the lateral surface of the solid, the boundary conditions can be imposed by requiring that it is unloaded,

$$ \begin{aligned} & \mathbf{t}_{R}=\mathbf{T}_{R} \mathbf{ n}=\mathbf{o}, \quad \mbox{for} \\ & X=\pm \frac{B}{2},\qquad Y\in \biggl[ -\frac{H}{2}, \frac{H}{2} \biggr] , \qquad Z\in \biggl[ -\frac{L}{2}, \frac{L}{2} \biggr] , \\ & X\in \biggl[ -\frac{B}{2}, \frac{B}{2} \biggr] ,\qquad Y=\pm \frac{H}{2}, \qquad Z\in \biggl[ -\frac{L}{2}, \frac{L}{2} \biggr] , \end{aligned} $$

(45)

where $\mathbf{t}_{R}$ is the Piola-Kirchhoff stress vector and $\mathbf{n}$ is the outward unit normal. Looking at the Piola-Kirchhoff stress tensor (31), hereafter rewritten in components for convenience, with $S=S_{X}=S_{Y}$ (given (14)):

$$ [\mathbf{T}_{R} ] =\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} S \cos \frac{X}{r} & -S \sin \frac{X}{r} & 0 \\ S \sin \frac{X}{r} \cos \frac{Z}{R_{0}} & S \cos \frac{X}{r} \cos \frac{Z}{R_{0}} & -S_{Z} \sin \frac{Z}{R_{0}} \\ S \sin \frac{X}{r} \sin \frac{Z}{R_{0}} & S \cos \frac{X}{r} \sin \frac{Z}{R_{0}} & S_{Z} \cos \frac{Z}{R_{0}} \end{array}\displaystyle \right ] , $$

(46)

it can be observed that: (i) to write the conditions (45) only the first two columns are used; (ii) the first two components $T_{R11}$ and $T_{R12}$ do not depend on the variable $Z$; (iii) again independently from $Z$, the components $T_{R21}$ and $T_{R22}$ , as well as the components $T_{R31}$ and $T_{R32}$, vanish when the terms $S \sin \frac{X}{r}$ and $S \cos \frac{X}{r}$ are zero, respectively. Previous observations allow a considerable simplification, since conditions (45) can be imposed for only one cross section of the solid, without considering the variability in Z. Therefore, choosing the cross section with $\mathit{Z}=0$, (45) reduces to

$$ \begin{aligned} &\mathrm{t}_{R\gamma } \biggl(\frac{B}{2}, Y, 0 \biggr)=0,\quad \forall Y\in \biggl[ -\frac{H}{2}, \frac{H}{2} \biggr] , \\ &\mathrm{t}_{R\gamma } \biggl(X, \frac{H}{2}, 0 \biggr)=0,\quad \forall X\in \biggl[ -\frac{B}{2}, \frac{B}{2} \biggr] , \\ &\mathrm{t}_{R\gamma } \biggl(-\frac{B}{2}, Y, 0 \biggr)=0,\quad \forall Y\in \biggl[ -\frac{H}{2}, \frac{H}{2} \biggr] , \\ &\mathrm{t}_{R\gamma } \biggl(X, -\frac{H}{2}, 0 \biggr)=0,\quad \forall X\in \biggl[ -\frac{B}{2}, \frac{B}{2} \biggr] , \end{aligned} $$

(47)

for $\gamma =1, 2$. At this point it is important to note that even for these boundary conditions, because a semi-inverse approach has been applied, it is not conceivable to satisfy them locally, namely, at each individual point of the boundary. In order to extract anyway some information from the equilibrium equations at the boundary, the nature of conditions (47) is transformed by imposing them in a global form by means of the following circulation integral:

$$\begin{aligned} &\frac{1}{2 ( B+H ) } \biggl\{ \int_{-\frac{H}{2}}^{\frac{H}{2}} \biggl[ \mathrm{t}_{R\gamma } \biggl( \frac{B}{2}, Y, 0 \biggr)- \mathrm{t}_{R\gamma } \biggl(-\frac{B}{2}, Y, 0 \biggr) \biggr] dY+ \int_{-\frac{B}{2}}^{\frac{B}{2}} \biggl[ \mathrm{t}_{R\gamma } \biggl(X, - \frac{H}{2}, 0 \biggr) \\ &\quad {}-\mathrm{t}_{R\gamma } \biggl(X, \frac{H}{2}, 0 \biggr) \biggr] dX \biggr\} =0. \end{aligned}$$

(48)

The calculus of this integral, carried out in the Appendix B, provides the following relationship:

$$ R_{0}-R=r \biggl( 1-\cos \frac{B}{2r} \biggr) . $$

(49)

Equilibrium conditions have been already exploited, reaching the equations (44) and (49), however, it still remains to determine the kinematic parameter $QN$. This last parameter can be evaluated by observing that, as already mentioned, it is numerically small and that the variation of the stretch $\lambda _{Y}$ along the depth of the cross section is quasi-rectilinear, even if this function has an exponential form. On the basis on these two observations, the following relationship can be written:

$$ \frac{1}{2} \bigl[ e^{-\frac{1}{r}(\frac{H}{2}+QN)}+e^{-\frac{1}{r}(- \frac{H}{2}+QN)} \bigr] \simeq 1, $$

(50)

from which it derives

$$ QN=r \ln \biggl[ \cosh \biggl( \frac{H}{2r} \biggr) \biggr] . $$

(51)

Ultimately, through the relations (44), (49) and (51), the three kinematic parameters $r$, $R$ and $QN$ may be evaluated and the displacement field (24) can be considered completely defined.

4 Eulerian Analysis

To assess stretches and stresses in the deformed configuration it is necessary to reverse the displacement field (24), with the purpose of expressing the Lagrangian coordinates $(X, Y, Z)$, used in the previous Section, in function of Eulerian coordinates $(x, y, z)$. Using (1) and (24), the Eulerian coordinates of a generic point of the body are

$$ \textstyle\begin{cases} x=X+u=r e^{-\frac{1}{r}(Y+QN)} \sin \frac{X}{r} \\ y=Y+v=-R-QN+ [ R+r-r e^{-\frac{1}{r}(Y+QN)}\cos \frac{X}{r} ] \cos \frac{Z}{R_{0}} \\ z=Z+w= [ R+r-r e^{-\frac{1}{r}(Y+QN)}\cos \frac{X}{r} ] \sin \frac{Z}{R_{0}}. \end{cases} $$

(52)

The inversion of this coupled system provides¹³

$$ \textstyle\begin{cases} X=r \arctan [ \frac{x}{R+r-\frac{y+R+QN}{\cos ( \arctan \frac{z}{y+R+QN} ) }} ] \\ Y=-QN-r \ln ( \frac{1}{r\cos \{ \arctan [ \frac{x}{R+r-\frac{y+R+QN}{ \cos ( \arctan \frac{z}{y+R+QN} ) }} ] \} } [ R+r-\frac{y+R+QN}{ \cos [ \arctan ( \frac{z}{y+R+QN} ) ] } ] ) \\ Z=R_{0}\arctan ( \frac{z}{y+R+QN} ) . \end{cases} $$

(53)

Although these equations have a rather complicated form, they formally allow the transition from Lagrangian coordinates to Eulerian coordinates.

The middle cross section $Z=0$ is the only cross section that does not rotate. It therefore does not exhibit displacements outside its plane, but only displacements in its plane. For this cross section the system (53) becomes

$$ \textstyle\begin{cases} X=r \arctan [ \frac{x}{r-y-QN} ] \\ Y=-QN-r \ln ( \frac{1}{r\cos \{ \arctan [ \frac{x}{r-y-QN} ] \} } [ r-y-QN ] ) \\ Z=0. \end{cases} $$

(54)

Employing (52), Fig. 7 shows the shape assumed by the middle cross section of the reference case in the deformed configuration (here and thereafter, the reference case is characterized by the following parameters: $B=2$, $H=1$, $L=10$ and $\alpha_{0}=\pi /3$. These geometrical parameters have to be considered dimensionless). In particular, this figure highlights the anticlastic effect.

Fig. 7

Middle cross section of the reference case in the deformed configuration

For the vertical line $x=0$ of the middle cross section, in Fig. 8 the diagrams of the stretches $\lambda_{z}$ and $\lambda$ are plotted. These stretches, assessed in the deformed configuration, were obtained by replacing (54) in (22). It is important to note from Fig. 8 that the graphs of stretches are exactly rectilinear, in fact, they assume the following expressions:

$$ \lambda_{z}=\frac{1}{R_{0}} ( R+y+QN ) , \quad \quad \lambda = \frac{1}{r} ( r-y-QN ) . $$

(55)

Fig. 8

Diagrams of the stretches minus one along the line $x=z=0$ for the reference case. (a) Longitudinal stretch $\lambda_{z}$. (b) Transversal stretch $\lambda$

Moreover, also the stretches plotted for the other vertical lines, i.e., by varying the variable $x$, show diagrams qualitatively straight. And this occurs for a wide range of geometric and constitutive parameters. The stretch $\lambda_{z}$ is unitary for $y=0.0349941$. The stretch $\lambda$ is unitary for a different value: $y=-0.0116366$. Figure 9 highlights the line of points with $\lambda_{z}=1$. Even it is substantially rectilinear. This straight line can be considered as the neutral axis for the deformation.¹⁴

Fig. 9

Line of points with $\lambda_{z}=1$

The practically straight developments obtained for stretches and for the neutral axis are consistent with the proposed kinematic model, based on the hypothesis of the planarity preservation for all cross sections after deformation. Such a hypothesis, as mentioned at the beginning, requires that cross sections maintain plane and rotate rigidly around the neutral axis. The rotation is finite. Within each cross section, it can then be observed the deformation generated by the anticlastic bending and described by the curvature $1/r$. These kinematic aspects become evident only when the deformed configurations of cross sections are considered. In other words, these aspects are not perceived with the use of Lagrangian coordinates.

Leaving now the middle cross section, we turn to examine the deformation along the longitudinal axis of the solid. In Fig. 10, some diagrams of the stretch $\lambda_{z}$ minus one are shown for discrete values of the variable $z$, taking fixed the variable $x$ ($X=x=0$). In this last figure, the reference case is always considered, but the angle $\alpha_{0}$ is now set equal to $\pi /2$. As it can be noted, the diagrams of $\lambda_{z}$ are substantially rectilinear. The pair of numerical values of $\lambda_{z}$ at the upper fiber ($\lambda_{z,\max}$) and at the lower fiber ($\lambda_{z,\min}$) is: (1.13461251, 0.8209771) for the cross section 1 ($\alpha =0$); (1.13461252, 0.8209773) for the cross section 2 ($\alpha =\pi /4$) and (1.13461251, 0.8209771) for the cross section 3 ($\alpha =\pi /2$). This first part of the Section, that deals with the kinematics in the deformed configuration, can be concluded by noting that the obtained formulae reproduce exactly the same graphics of stretches for all cross sections of the solid.

Fig. 10

Longitudinal distribution of stretches $\lambda_{z}$ in the deformed configuration. Reference case with $\alpha_{0}=\pi /2$

The stress measure, coherently employed in the spatial configuration, is that of Cauchy. The Cauchy stress tensor T is obtained from the Piola-Kirchhoff stress tensor $\mathbf{T}_{R}$ through the well-known transformation

$$ \mathbf{T}_{R}=\mathbf{TF}^{\star }. $$

(56)

Using (25), (26), (31) and (56), the following components are computed ($S=S_{x}=S_{y}$, $\lambda =\lambda_{x}=\lambda_{y}$):

$$ (\det \mathbf{F}) [ \mathbf{T} ] =\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} S \lambda & 0 & 0 \\ 0 & S \lambda \cos^{2}\frac{Z}{R_{0}}+S_{z} \lambda_{z} \sin^{2}\frac{Z}{R _{0}} & (S \lambda -S_{z} \lambda_{z}) \sin \frac{Z}{R_{0}} \cos \frac{Z}{R_{0}} \\ 0 & (S \lambda -S_{z} \lambda_{z}) \sin \frac{Z}{R_{0}} \cos \frac{Z}{R _{0}} & S \lambda \sin^{2}\frac{Z}{R_{0}}+S_{z} \lambda_{z} \cos ^{2}\frac{Z}{R_{0}} \end{array}\displaystyle \right ] . $$

(57)

The tensor T is symmetric. The matrix (57) can be rewritten in diagonal form by evaluating its eigenvalues. The resolution of the characteristic polynomial allows the determination of the principal stresses in the deformed configuration

$$ [ \mathbf{T} ] =\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{S}{\lambda \lambda_{z}} & 0 & 0 \\ 0 & \frac{S}{\lambda \lambda_{z}} & 0 \\ 0 & 0 & \frac{S_{z}}{\lambda^{2}} \end{array}\displaystyle \right ] , $$

(58)

where

$$ \begin{aligned} &T_{1}=T_{2}= \frac{S}{\lambda \lambda_{z}}=\frac{2}{ \lambda_{z}} \bigl[ \omega_{1}+ \bigl( \lambda^{2}+\lambda_{z}^{2} \bigr) \omega_{2}+\lambda^{2}\lambda_{z}^{2} \omega_{3} \bigr] , \\ &T_{3}=\frac{\mathit{S_{z}}}{\lambda^{2}}=\frac{2}{\lambda ^{2}} \bigl[ \lambda_{z} \omega_{1}+2\lambda^{2} \lambda_{z} \omega _{2}+\lambda^{4} \lambda_{z} \omega_{3} \bigr] . \end{aligned} $$

(59)

The principal directions of stress are the eigenvectors associated with these eigenvalues. The principal direction corresponding to the eigenvalue $T_{3}$ is the unit vector orthogonal to the plane $\Omega$ (cf. Fig. 4) with components (0, $-\sin \frac{Z}{R_{0}}$, $\cos \frac{Z}{R_{0}}$). The other two eigenvectors are any two unit vectors orthogonal to each other and belonging to the plane $\Omega$. Substituting (40) and (42) in (59), the principal stresses become

$$ \begin{aligned} &T_{1}=T_{2}= \frac{2}{\lambda^{2} \lambda_{z}} \bigl\{ \bigl( \lambda ^{2}-1 \bigr) a+ \bigl[ \bigl( \lambda^{2}+ \lambda_{z}^{2} \bigr) \lambda^{2}-2 \bigr] b+ \bigl(\lambda^{4} \lambda_{z}^{2}-1 \bigr) c \bigr\} , \\ &T_{3}=\frac{2}{\lambda^{2} \lambda_{z}} \bigl\{ \bigl(\lambda_{z} ^{2}-1 \bigr)a+2 \bigl(\lambda^{2} \lambda_{z}^{2}-1 \bigr)b+ \bigl( \lambda^{4}\lambda_{z}^{2}-1 \bigr) c \bigr\} . \end{aligned} $$

(60)

These expressions of the principal stresses of Cauchy for a compressible Mooney-Rivlin material will be used below for some numerical investigations. Note that in the absence of deformation these stresses vanish.

Stress distributions inside the solid may assume different shapes depending on the selected constitutive parameters. The influence exerted on stresses by the constant $b$, proportional to the area variation coefficients (cf. (39)), is shown in Fig. 11. Generally this parameter is not greater than $a$. Considering the reference case, Fig. 11 shows two diagrams of the stress along the line $x=z=0$, plotted for $b=0$ (compressible neo-Hookean material) and for $b=1$, while the other two constitutive constants are kept fixed and equal to: $a=1$ and $c=5$.¹⁵ The constant $a$, $b$ and $c$ have been considered dimensionless. From Fig. 11, it can be observed that there are no qualitative differences between the two diagrams: the stress $T_{3}$ grows by increasing $b$, whereas $T _{1}$ remains substantially unchanged.

Fig. 11

Diagrams of Cauchy principal stresses along the line $x=z=0$ for the reference case with different values of the constitutive parameter $b$. (a) $b=0$. (b) $b=1$

The variation of the constitutive parameter $c$ involves a more articulated scenario. This parameter is related to the change of volume and it can take larger values than the parameter $a$. Increasing the constant $c$, the constitutive law tends toward an internal condition of incompressibility ($\det \mathbf{F}=1$), but without reaching it completely. This occurrence can be observed in Fig. 12, where the ratio $\delta$, between an infinitesimal volume of the solid after deformation $dv$ and before deformation $dv_{0}$ ($\delta =\frac{dv}{dv_{0}}=\det \mathbf{F}= \lambda^{2}\lambda_{z}$), is evaluated along the line $x=z=0$ by varying the parameter $c$. From Fig. 12 it may be observed that, in the case of $c=100$, the ratio $\delta$ tends to assume for all points a value just lower than one. This means that an almost uniform volumetric contraction occurs in the bending of the solid. On the other hand, for $c=1$, in the upper part of the cross section volumetric dilatations ($\delta >1$) appear, which varying locally increase approaching the upper edge. Similarly, the lower part of the cross section exhibits volumetric contractions ($\delta <1$) that increase approaching the bottom edge. The behavior just described for the cases with $c=1$ seems to be more natural for compressible solids.

Fig. 12

Diagrams of the ratio $\delta =dv/dv_{0}$ along the line $x=z=0$ for the reference case with different values of the constitutive parameter $c$

The six images in Fig. 13 display the stress diagrams for $c=0.1, 1, 5, 10, 23, 100$. For low values of $c$, $T_{3}$ has a linear development and $T_{1}$ is almost zero. For mean values of $c$, $T_{3}$ and $T_{1}$ assume a curved shape, with $T_{3}$ (in absolute value and in most part of the diagram) greater than $T_{1}$. For high values of $c$, the diagrams assume forms increasingly concave. In particular, for $c=23$, $T_{3}$ has no null points. $T_{1}$ grows and assumes values similar to those of $T_{3}$ for $c=100$, so reproducing a hydrostatic state of stress $(T_{1}=T_{2}=T_{3}<0)$. For these last cases, in the formulae (60), the third term, equal in both expressions, becomes predominant with respect to the first two. Namely, in the constitutive law, contributions to the stress due to the volume variations are prevailing. Here, it should be noted that these stress distributions due to high values of $c$, in the case of an inflexed solid, appear to be totally unrealistic.

Fig. 13

Diagrams of Cauchy principal stresses along the line $x=z=0$ for the reference case with different values of the constitutive parameter $c$. (a) $c=0.1$. (b) $c=1$. (c) $c=5$. (d) $c=10$. (e) $c=23$. (f) $c=100$

Having established a range of variation physically plausible for the constitutive parameter $c$, we turn to control numerically the obtained solution, having now the possibility to also investigate the stress distributions in the deformed configuration. The plots of Figs. 14, 15 and 16 are related to the reference case with the values of the parameter $c$ equal to 0.1, 1 and 5, respectively.

Fig. 14

Numerical check of the obtained solution. Case with $c=0.1$. Plots for the deformed cross section $z=0$. Adopted parameters: $B=2,H=1$, $L=10$ and $\alpha_{0}=\pi /3$ (kinematic); $a=1$, $b=0.5$ (constitutive). (a) Equilibrium equation along the $X$ axis. (b) Equilibrium equation along the $Y$ axis. (c) Cauchy principal stress $T_{33}$. (d) Cauchy principal stresses $T_{11}=T _{22}$

Fig. 15

Numerical check of the obtained solution. Case with $c=1$. Plots for the deformed cross section $z=0$. Adopted parameters: $B=2,H=1$, $L=10$ and $\alpha_{0}=\pi /3$ (kinematic); $a=1$, $b=0.5$ (constitutive). (a) Equilibrium equation along the $X$ axis. (b) Equilibrium equation along the $Y$ axis. (c) Cauchy principal stress $T_{33}$. (d) Cauchy principal stresses $T_{11}=T _{22}$

Fig. 16

Numerical check of the obtained solution. Case with $c=5$. Plots for the deformed cross section $z=0$. Adopted parameters: $B=2,H=1$, $L=10$ and $\alpha_{0}=\pi /3$ (kinematic); $a=1$, $b=0.5$ (constitutive). (a) Equilibrium equation along the $X$ axis. (b) Equilibrium equation along the $Y$ axis. (c) Cauchy principal stress $T_{33}$. (d) Cauchy principal stresses $T_{11}=T _{22}$

The diagrams of Fig. 14(a) and 14(b), relating to the case $c=0.1$, show that the equilibrium equations along the $X$ and $Y$ axes can be considered fulfilled in all points of the cross section, being the numerical values very close to zero.¹⁶ Fig. 14(d) highlights that the Cauchy principal stresses $T_{1}= T_{2}$ are practically null. In particular, these values are also null at the boundary of the cross section, thus satisfying the boundary condition which requires that the lateral surface of the solid is unloaded. Definitively, the equilibrium solution for $c=0.1$ is very accurate.

Figure 15 illustrates the case $c=1$, that is the case in which the two non-normalized constants $a$ and $c$ coincide. The equilibrium along the $X$ axis is well satisfied for all points of the cross section (cf. Fig. 15(a)), while the equilibrium along the $Y$ axis shows some slight approximations approaching the upper and the lower edge (cf. Fig. 15(b)). Stresses $T_{1}=T_{2}$ are still close to zero (cf. Fig. 15(d)) and overall the solution can be considered still accurate.

In the case with $c=5$, shown in Fig. 16, numerical approximations become more evident. The equilibrium equations are well satisfied only in the central core of the cross section. Stresses $T_{1}=T_{2}$ remain small only at the left and right edges of cross section (cf. Fig. 16(d)). Therefore, the value $c=5$ for the reference case can be regarded as the upper limit for the numerical accuracy of the solution.¹⁷

In Fig. 17, for the middle cross section in its deformed configuration, the neutral axis for the deformation (points with $\lambda_{z}=1$) and the neutral line for the stress (points with $T_{3}=0$) are compared. As can be observed, for low values of $c$, the two lines practically coincide. In this case, the neutral line for the stress is practically straight. Instead, for mean values of $c$, the two lines turn away in the central portion of the cross section and, for high values of $c$ (cases physically unrealistic), two lateral neutral lines for the stress appear.

Fig. 17

Comparison between the neutral axis for the deformation and the neutral line for stress in the middle cross section for the reference case with different values of the constitutive parameter $c$. (a) $c=0.1$. (b) $c=1$. (c) $c=5$. (d) $c=10$. (e) $c=23$. (f) $c=100$

The longitudinal diagrams of the stress $T_{3}$ are shown in Fig. 18 for the reference case with $\alpha =\pi /2$. As in the case of the stretches illustrated by Fig. 10, the stress diagrams are all equal. At the upper fiber, $T_{3}=0.40831$ (tensile), while at the lower fiber $T_{3}=-2.39005$ (compression).

Fig. 18

Longitudinal diagrams of the stress $T_{3}$ in the deformed configuration. Reference case with $\alpha_{0}=\pi /2$

Knowing the stress distributions, the normal force $n$ and the bending moment $m_{x}$ can be evaluated. Using a polar coordinate system $(\rho , \theta )$ with pole at the point $C_{2}$ of Fig. 4, for the generic deformed cross section the following expressions are derived:

$$ n= \int_{-\beta_{0}}^{\beta_{0}} \int_{\rho_{\min}}^{\rho_{\max}} \rho T_{3}(\rho , \theta ) d\rho d\theta , \qquad m_{x}= \int_{-\beta_{0}}^{\beta_{0}} \int_{\rho_{\min}}^{\rho_{\max}} \rho T_{3}(\rho , \theta ) \tilde{y} d\rho d\theta , $$

(61)

where $x=\rho \sin \theta$, $\tilde{y}=r-QN-\rho \cos \theta$, $\rho_{\min}=r e^{-\frac{H+2 QN}{2r}}$, $\rho_{\max}=r e^{\frac{H-2 QN}{2r}}$.

In Fig. 19 the calculations performed to evaluate the normal force $n$ are reported. The two upper curves are related to the limit case $c=5$, those lower to the case $c=0.1$. As can be observed, the normal force $n$ is small, but it becomes even smaller for $\alpha_{0}$ decreasing or $L$ increasing.

Fig. 19

Plot of the normal force $n$ versus the curvature $1/r$

Using the expression (61)₂, the diagram plotted in Fig. 20 has been obtained. In this figure, for the middle cross section¹⁸ and for the reference case, the moment $m_{x}$ is assessed numerically by varying the angle $\alpha_{0}$. On the basis of this result, the boundary conditions at the two end faces can be set geometrically by means of the angle $\alpha_{0}$ or statically through the application of the corresponding moment $m_{x}$.

Fig. 20

Plot of the bending moment $m_{x}$ versus the angle $\alpha_{0}$

5 Infinitesimal Fields

From a finite (or nonlinear) theory an infinitesimal (or linearized) theory can be derived by introducing two fundamental hypotheses, which require that both the displacement and the displacement gradient fields are small.

In order to linearize the formulation, all formulas derived in the previous sections will be developed in power series as functions of the radii $r$ and $R_{0}$. These series will be truncated preserving the infinitesimals of order $\mathcal{O}(r^{-1})$ and $\mathcal{O}(R_{0} ^{-1})$ as $r\rightarrow \infty$ or $R_{0}\rightarrow \infty$. Operatively, the following series expansions will be employed:¹⁹

$$\begin{aligned} &QN\simeq \frac{H^{2}}{8 r}+o \bigl(r^{-2} \bigr),\qquad R_{0}-R\simeq \frac{B^{2}}{8 r}+o \bigl(r^{-2} \bigr), \\ &e^{-\frac{1}{r}(Y+QN)}\simeq 1-\frac{Y}{r}-\frac{H^{2}}{8 r^{2}}+ \frac{Y ^{2}}{8 r^{2}}+o \bigl(r^{-3} \bigr),\qquad \sin \frac{X}{r} \simeq \frac{X}{r}+o \bigl(r ^{-2} \bigr), \\ & \cos \frac{X}{r}\simeq 1-\frac{X^{2}}{2 r^{2}}+o \bigl(r^{-3} \bigr), \quad \quad \sin \frac{Z}{R_{0}}\simeq \frac{Z}{R_{0}}+o \bigl(R_{0}^{-2} \bigr),\\ & \cos \frac{Z}{R _{0}}\simeq 1-\frac{Z^{2}}{2 R_{0}^{2}}+o \bigl(R_{0}^{-3} \bigr), \quad \quad R \sin \frac{Z}{R_{0}}\simeq Z-\frac{Z B^{2}}{8 r R_{0}}-\frac{Z ^{3}}{6 R_{0}^{2}}+o \bigl(R_{0}^{-2} \bigr), \\ & R \cos \frac{Z}{R_{0}} \simeq R-\frac{Z^{2}}{2 R_{0}}+o \bigl(R_{0}^{-2} \bigr),\qquad \sinh \frac{H}{2 r} \simeq \frac{H}{2 r}+o \bigl(r^{-2} \bigr). \end{aligned}$$

(62)

Using (62), the displacement field (24) can be approximated as

$$ \begin{aligned} u&\simeq -X+r \biggl(1-\frac{Y}{r}- \frac{H^{2}}{8 r^{2}}+ \frac{Y^{2}}{8 r ^{2}}+o \bigl(r^{-3} \bigr) \biggr) \biggl( \frac{X}{r}+o \bigl(r^{-2} \bigr) \biggr)\simeq - \frac{XY}{r}+o \bigl(r^{-1} \bigr), \\ v&\simeq -Y-R-\frac{H^{2}}{8 r}+o \bigl(r^{-2} \bigr)+ \biggl[ R+r-r \biggl(1-\frac{Y}{r}-\frac{H ^{2}}{8 r^{2}}+\frac{Y^{2}}{8 r^{2}}+o \bigl(r^{-3} \bigr) \biggr) \\ &\phantom{\simeq\,\,}{} \times \biggl(1-\frac{X^{2}}{2 r ^{2}}+o \bigl(r^{-3} \bigr) \biggr) \biggr] \biggl(1-\frac{Z^{2}}{2 R_{0}^{2}}+o \bigl(R_{0}^{-3} \bigr) \biggr)\\&\simeq -\frac{Y ^{2}}{2 r}+\frac{X^{2}}{2 r}-\frac{Z^{2}}{2 R_{0}}+o \bigl(r^{-1} \bigr)+o \bigl(R _{0}^{-1} \bigr), \\ w&\simeq -Z+ \biggl[ R+r-r \biggl(1-\frac{Y}{r}-\frac{H^{2}}{8 r^{2}}+ \frac{Y ^{2}}{8 r^{2}}+o \bigl(r^{-3} \bigr) \biggr) \biggl(1- \frac{X^{2}}{2 r^{2}}+o \bigl(r^{-3} \bigr) \biggr) \biggr] \\ &\phantom{\simeq\,\,}{} \times \biggl(\frac{Z}{R_{0}}+o \bigl(R_{0}^{-2} \bigr) \biggr)\simeq \frac{YZ}{R_{0}}+o \bigl(r^{-1} \bigr)+o \bigl(R _{0}^{-1} \bigr), \end{aligned} $$

(63)

having neglected the infinitesimal terms of higher order than $r^{-1}$ and $R_{0}^{-1}$. In the linearized theory of inflexed beams, the following two relationships hold:²⁰

$$ \frac{1}{R_{0}}=\frac{M_{X}}{E J_{X}},\quad \quad r=\frac{R_{0}}{\nu }, $$

(64)

where $M_{X}$ denotes the bending moment around the $X$ axis, $J_{X}$ the moment of inertia of the cross section with respect to the $X$ axis, $E$ the Young’s modulus and $\nu$ the Poisson’s ratio. Introducing (64) into (63), the infinitesimal displacement field is finally derived²¹

$$ \textstyle\begin{cases} u=-\frac{\nu M_{X}}{E J_{X}} XY \\ v=\frac{1}{2} \frac{M_{X}}{E J_{X}}(\nu X^{2}-\nu Y^{2}-Z^{2}) \\ w=\frac{M_{X}}{E J_{X}} YZ, \end{cases} $$

(65)

in the classic form which can be found in any textbook (see, e.g., system (7.28) at p. 184 of [31]).

Computing from (63) the displacement gradient H,

$$ [ \mathbf{H} ] = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} -\frac{Y}{r} & -\frac{X}{r} & 0 \\ \frac{X}{r} & -\frac{Y}{r} & -\frac{Z}{R_{0}} \\ 0 & \frac{Z}{R_{0}} & \frac{Y}{R_{0}} \end{array}\displaystyle \right ] , $$

(66)

and applying then the theorem of additive decomposition, the symmetric tensor of infinitesimal strain E and the skew-symmetric tensor of infinitesimal rigid rotation W are obtained

$$\begin{aligned} & [ \mathbf{E} ] = \biggl[\frac{1}{2} \bigl( \mathbf{H}+ \mathbf{H}^{ T} \bigr) \biggr]=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \varepsilon_{x} & \frac{1}{2}\gamma_{xy} & \frac{1}{2}\gamma_{xz} \\ \frac{1}{2}\gamma_{xy} & \varepsilon_{y} & \frac{1}{2}\gamma_{yz} \\ \frac{1}{2}\gamma_{xz} & \frac{1}{2}\gamma_{yz} & \varepsilon_{z} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} -\frac{Y}{r} & 0 & 0 \\ 0 & -\frac{Y}{r} & 0 \\ 0 & 0 & \frac{Y}{R_{0}} \end{array}\displaystyle \right ] , \end{aligned}$$

(67)

$$\begin{aligned} & [ \mathbf{W} ] = \biggl[\frac{1}{2} \bigl( \mathbf{H}- \mathbf{H}^{ T} \bigr) \biggr]=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & -\omega_{z} & \omega_{y} \\ \omega_{z} & 0 & -\omega_{x} \\ -\omega_{y} & \omega_{x} & 0 \end{array}\displaystyle \right ] =\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & -\frac{X}{r} & 0 \\ \frac{X}{r} & 0 & -\frac{Z}{R_{0}} \\ 0 & \frac{Z}{R_{0}} & 0 \end{array}\displaystyle \right ] . \end{aligned}$$

(68)

The linearized strain state is triaxial and principal, it depends (linearly) only on the variable $Y$ and vanishes for $Y=0$. Among components of the tensor W, the rotation $\alpha$ around the $X$ axis and $\beta$ around the $Z$ axis are recognizable. Using (62), the deformation gradient (25) can be rewritten in the following approximated form:²²

$$ [ \mathbf{F} ] =\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1-\frac{Y}{r} & -\frac{X}{r} & 0 \\ \frac{X}{r} & 1-\frac{Y}{r} & -\frac{Z}{R_{0}} \\ 0 & \frac{Z}{R_{0}} & 1+\frac{Y}{R_{0}} \end{array}\displaystyle \right ] . $$

(69)

In the same way, the linearization of tensors (26) and (27) gives the following relationships:²³

$$ \begin{aligned} & [ \mathbf{R} ] \simeq \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1 & -\frac{X}{r} & 0 \\ \frac{X}{r} & 1 & -\frac{Z}{R_{0}} \\ 0 & \frac{Z}{R_{0}} & 1 \end{array}\displaystyle \right ] \equiv [\mathbf{I}+ \mathbf{W}], \\ & [ \mathbf{U} ] \simeq \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 1-\frac{Y}{r} & 0 & 0 \\ 0 & 1-\frac{Y}{r} & 0 \\ 0 & 0 & 1+\frac{Y}{R_{0}} \end{array}\displaystyle \right ] \equiv [\mathbf{I}+ \mathbf{E}]. \end{aligned} $$

(70)

Let us now turn to stresses. With the linearization, the Piola-Kirchhoff stress tensor becomes

$$ [ \mathbf{T}_{R} ] =\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} S \cos \frac{X}{r} & -S \sin \frac{X}{r} & 0 \\ S \sin \frac{X}{r} \cos \frac{Z}{R_{0}} & S \cos \frac{X}{r} \cos \frac{Z}{R_{0}} & -S_{Z} \sin \frac{Z}{R_{0}} \\ S \sin \frac{X}{r} \sin \frac{Z}{R_{0}} & S \cos \frac{X}{r} \sin \frac{Z}{R_{0}} & S_{Z} \cos \frac{Z}{R_{0}} \end{array}\displaystyle \right ] \simeq \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} S & 0 & 0 \\ 0 & S & 0 \\ 0 & 0 & S_{Z} \end{array}\displaystyle \right ] , $$

(71)

where²⁴

$$ \begin{aligned} T_{R_{1}} &=T_{R_{2}}=S=2a \lambda +2b \lambda^{3}+2b \lambda \lambda _{Z}^{2}+2c \lambda^{3} \lambda_{Z}^{2}-\frac{d}{\lambda } \\&\simeq -(4a+12b+8c) \frac{Y}{r}+(4b+4c) \frac{Y}{R_{0}}, \\ T_{R_{3}}&=S_{Z}=2a \lambda_{Z}+4b \lambda^{2}\lambda_{Z}+2c \lambda ^{4} \lambda_{Z}-\frac{d}{\lambda_{Z}}\simeq -(8b+8c) \frac{Y}{r}+(4a+8b+4c) \frac{Y}{R_{0}}. \end{aligned} $$

(72)

The linearized Piola-Kirchhoff stress state is triaxial and principal, it depends (linearly) only on the variable $Y$ and vanishes for $Y=0$. The linearization of the Cauchy stress components (60) gives²⁵

$$ \begin{aligned} T_{1}&=T_{2}= \frac{2}{\lambda^{2} \lambda_{z}} \bigl\{ \bigl(\lambda^{2}-1 \bigr)\mathit{ a}+ \bigl[ \bigl( \lambda^{2}+\lambda_{z}^{2} \bigr) \lambda^{2}-2 \bigr] \mathit{ b}+ \bigl(\lambda^{4} \lambda_{z}^{2}-1 \bigr) \mathit{c} \bigr\} \\&\simeq -(4a+12b+8c) \frac{Y}{r}+(4b+4c) \frac{Y}{R_{0}}, \\ T_{3}&=\frac{2}{\lambda^{2} \lambda_{z}} \bigl\{ \bigl(\lambda_{z} ^{2}-1 \bigr)\mathit{ a}+2 \bigl(\lambda^{2} \lambda_{z}^{2}-1 \bigr)\mathit{ b}+ \bigl( \lambda^{4}\lambda_{z}^{2}-1 \bigr) \mathit{c} \bigr\} \\& \simeq -(8b+8c) \frac{Y}{r}+(4a+8b+4c) \frac{Y}{R_{0}}. \end{aligned} $$

(73)

These components coincide with (72), showing, as well known, that in the infinitesimal theory the two stress measures coincide. Moreover, the neutral axis of strain coincides with that of the stress and they pass through the centroid of the cross section.

Obviously, the above stresses (72) and (73) are different from those of the usual linearized theory, since the constitutive laws used are different. However, certain conditions can be established for the constitutive parameters $a$, $b$ and $c$ of a compressible Mooney-Rivlin material so as to reproduce the stresses provided by the Navier’s inverse relationships, which are the constitutive law commonly used in the infinitesimal theory,

$$ \bar{\mathbf{T}}=2G \mathbf{E}+\bar{\lambda }(\mathrm{tr}\mathbf{E}) \mathbf{I}, $$

(74)

where $G$ and $\bar{\lambda }$ are the Lamé constants and $\mathrm{tr}\mathbf{E}=\varepsilon_{x}+\varepsilon_{y}+\varepsilon_{z}$. The diagonal components of $\bar{\mathbf{T}}$ are denoted by $\sigma_{x}, \sigma_{y}, \sigma_{z}$. Equaling the component $\sigma_{x}$ of (74) with the linearized expression (72)₁ of $S$, the following relations are obtained:

$$ \textstyle\begin{cases} G=2(a+b), \\ \bar{\lambda }=4(b+c). \end{cases} $$

(75)

The Lamé constants $G$ and $\bar{\lambda }$ can be thus converted into the pair of elastic constants $E$ and $\nu$

$$ \textstyle\begin{cases} E=\frac{G (3\bar{\lambda }+2G)}{\bar{\lambda }+G}= \frac{4(a+b)(a+4b+3c)}{a+3b+2c}, \\ \nu =\frac{\bar{\lambda }}{2(\bar{\lambda }+G)}=\frac{b+c}{a+3b+2c}. \end{cases} $$

(76)

Introducing the strain tensor E, in the form specified by (67), into the constitutive law (74) and using relations (64)₂ and (76), the stress tensor $\bar{\mathbf{T}}$ assumes the following form:

$$ [\bar{\mathbf{T}}]=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & E \varepsilon_{z} \end{array}\displaystyle \right ] , $$

(77)

showing, as well known, that in the linearized theory the stress state is uniaxial being different from zero only the component $\sigma_{z}$.²⁶

With this last step, the linearization procedure which leads from the finite anticlastic bending of a solid to the well-know infinitesimal bending of a beam is completed.

6 Conclusions

The most popular mathematical model for inflexed solids, with both large deformation and displacement fields, was proposed by Rivlin [15]. This model, formulated under the plane displacement condition, does not allow to describe the transversal deformation of cross sections, which in such a model preserve their shape and size and undergo only finite rotations. On the contrary, from a purely physical point of view, the longitudinal inflexion of a solid is always associated with a traversal inflexion, known as anticlastic effect (cf. Fig. 1b).

In the fully nonlinear context of finite elasticity, this paper extends the aforementioned models, because the bending of a solid is described by a three-dimensional displacement field which takes into account the transversal pure deformation of cross sections.

Adopting a semi-inverse approach, this three-dimensional displacement field is defined by a kinematical model based on the following assumptions: the solid is inflexed longitudinally with constant curvature; after deformation, cross sections maintain their planarity and are inflexed in their plane with constant curvature. The kinematic model has three free parameters, which are determined imposing the equilibrium conditions.

Despite the elaborate shape of the displacement field, the stretches resulting from it have simple and compact expressions in terms of exponential functions (cf. Eq. (22)). The deformation state is triaxial and non-homogeneous.

The compressible Mooney-Rivlin law has been assigned to the stored energy function. Once determined the Piola-Kirchhoff stress tensor $\mathbf{T}_{R}$, the equilibrium equations have been derived. But, having adopted the semi-inverse method, i.e., in practice having assigned for hypothesis the shape of solution a priori, it is inconceivable that the equilibrium equations can be correctly solved for all points of the solid. Nevertheless, a basic longitudinal line has been recognized, where the compatibility and equilibrium conditions are fully satisfied.

To assess the accuracy of the displacement field in correspondence of the other points, the equilibrium equations were normalized and, by means of numerical analyses, it was estimated how much they deviate from zero as one moves away from the basic line. Through a set of diagrams, the existence of a central core surrounding the basic line, where the solution proposed can be considered acceptable, has been highlighted. The extension of this central core depends on the parameters involved. The most important geometric parameters are the length of the solid $L$ and the angle of inflexion $\alpha_{0}$, because the central core becomes wider as $L$ increases and as $\alpha_{0}$ decreases.

Once completed the Lagrangian analysis, the Eulerian analysis was conducted with the purpose of evaluating stretches and stresses in the deformed configuration. The expressions of the Cauchy principal stresses have been obtained (cf. Eq. (60)) and the effective stress distributions in the inflexed solid are shown by some diagrams. Successively, the influence exerted on these stresses by the normalized constitutive parameters $b$ and $c$ have been investigated (cf. Figs. 11 and 13).

The parameter $b$ does not exert a qualitative influence on the stress distributions in cross sections. More care is needed for the parameter $c$. When the parameter $c$ is small or at most equal to the first constitutive parameter $a$, the obtained solution is numerically accurate, since the equilibrium equations are well satisfied for all points of the cross sections and the lateral surface of the solid is unloaded (cf. Figs. 14 and 15). Increasing the value of the parameter $c$, the approximations become more evident. The case $c=5$ may be considered the upper limit for a numerically accurate solution (cf. Fig. 16).

By varying the parameter $c$, a comparison was made between the neutral line for the stress ($T_{3}=0$) and the neutral axis for the deformation ($\lambda_{z}=1$). For low values of $c$, the two lines coincide. For average values of $c$, the two lines differ. In particular, the neutral line for the stress assumes a curved shape. For high values of $c$ (cases physically unrealistic), two distinct neutral lines for the stress even appear (cf. Fig. 17).

Knowing the stress distributions, explicit formulae to calculate the normal force and the bending moment in the deformed configuration were given (cf. Eq. (61)). A further verification of the obtained solution was made by checking that the normal force is close to zero. Being available the expression for the bending moment, the value of the moment needed to produce a specific inflexion angle $\alpha_{0}$ can be assessed. This allows to impose the boundary conditions statically, through the application on the two end faces of the solid of a pair of bending moments (cf. Fig. 20).

The whole formulation exposed in the paper for the finite anticlastic bending of hyperelastic solids was linearized by introducing the hypothesis of smallness of the displacement and strain fields. All derived formulae were rewritten as power series. These series, which depend on the radii $r$ and $R_{0}$, were truncated by preserving the first order infinitesimals as $r\rightarrow \infty$ and $R_{0}\rightarrow \infty$.

Operating in this way, the nonlinear displacement field (24) was linearized getting exactly the well-known displacement field of the linear theory of inflexed beams (cf. Eq. (65)).

Unlike to what was obtained using the finite theory, in the infinitesimal theory the neutral axis of strain coincides with the neutral line of the stress and they pass through the centroid of the cross section.

The linearization procedure, based on the assumptions of smallness, has shown the transition from the proposed solution for the finite anticlastic bending of solids to the classical solution for the infinitesimal bending of beams.

Appendices

Appendix A: Derivatives $S_{J,J}$

The derivatives $S_{J,J}$ of equilibrium equations (35) have the following expressions:

$$ \begin{aligned} S_{X,X}&=2 ( \omega_{1,X}+I_{1,X} \omega_{2}+I_{1} \omega_{2,X} ) \lambda_{X}-2 \omega_{2,X} \lambda_{X}^{3}+2 ( I_{3,X} \omega _{3}+I_{3} \omega_{3,X} ) \frac{1}{\lambda_{X}}, \\ S_{Y,Y}&=2 ( \omega_{1,Y}+I_{1,Y} \omega_{2}+I_{1} \omega_{2,Y} ) \lambda_{Y}+2 ( \omega_{1}+I_{1} \omega_{2} ) \lambda_{Y,Y}-2 \omega_{2,Y} \lambda_{Y}^{3} \\ &\phantom{=\,\,}{}-6 \omega_{2} \lambda_{Y}^{2} \lambda_{Y,Y}+2 I_{3,Y} \omega_{3} \frac{1}{\lambda_{Y}}+2 I_{3} \omega_{3,Y} \frac{1}{\lambda_{Y}}-2 I_{3} \omega_{3} \frac{\lambda_{Y,Y}}{\lambda_{Y}^{2}}, \\ S_{Z,Z}&=0, \end{aligned} $$

(78)

where $\omega_{i}=\frac{\partial \omega }{\partial I_{i}}$ for $i=1, 2, 3$, $I_{i,K}=\frac{\partial I_{i}}{\partial K}$ and $\omega_{i,K}=\frac{\partial }{\partial K} ( \frac{\partial \omega }{\partial I_{i}} )$ for $K=X, Y$, and with

$$\begin{aligned} & \lambda_{Y,Y}=\frac{\partial \lambda_{Y}}{\partial Y}=-\frac{1}{r} e ^{-\frac{1}{r}(Y+QN)}, \\ &I_{1,X}=2 \lambda_{Z} \frac{1}{R_{0}} e^{-\frac{1}{r}(Y+QN)} \sin \frac{X}{r}, \\ &I_{1,Y}=-\frac{4}{r} e^{-\frac{2}{r}(Y+QN)}+2 \lambda_{Z} \frac{1}{R _{0}} e^{-\frac{1}{r}(Y+QN)} \cos \frac{X}{r}, \\ &I_{3,X}=2 e^{-\frac{5}{r}(Y+QN)} \lambda_{Z} \frac{1}{R_{0}} \sin \frac{X}{r}, \\ & I_{3,Y}=-\frac{4}{r} e^{-\frac{4}{r}(Y+QN)} \lambda_{Z}^{2}+ 2 e ^{-\frac{5}{r}(Y+QN)} \lambda_{Z} \frac{1}{R_{0}} \cos \frac{X}{r}. \end{aligned}$$

For the longitudinal basic line ($X=0, Y=-QN$ and $Z=Z$), the previous derivatives simplify in:

$$ \begin{aligned} &S_{X,X}=2 \omega_{1,X}+2 \biggl[ 1+ \biggl( \frac{R}{R_{0}} \biggr) ^{2} \biggr] \omega_{2,X}+2 \biggl( \frac{R}{R_{0}} \biggr) ^{2} \omega_{3,X}, \\ &S_{Y,Y}=-\frac{2}{r} \omega_{1}+2 \omega_{1,Y}+ \biggl[ -\frac{6}{r}+4\frac{R}{R _{0}^{2}}- \frac{2}{r} \biggl( \frac{R}{R_{0}} \biggr) ^{2} \biggr] \omega _{2}+2 \biggl[ 1+ \biggl( \frac{R}{R_{0}} \biggr) ^{2} \biggr] \omega_{2,Y}\\ &\phantom{S_{Y,Y}=\,\,}{}+ \biggl[ 4\frac{R}{R_{0}^{2}}- \frac{6}{r} \biggl( \frac{R}{R_{0}} \biggr) ^{2} \biggr] \omega_{3}+2 \biggl( \frac{R}{R_{0}} \biggr) ^{2} \omega_{3,Y}, \\ & S_{Z,Z}=0, \end{aligned} $$

(79)

with

$$\begin{aligned} & I_{1}=2+ \biggl( \frac{R}{R_{0}} \biggr) ^{2},\qquad I_{1,X}=0,\qquad I_{1,Y}=- \frac{4}{r}+ \frac{2R}{R_{0}^{2}}, \\ & I_{3}= \biggl( \frac{R}{R_{0}} \biggr) ,\qquad I_{3,X}=0,\qquad I_{3,Y}=- \frac{4}{r} \biggl( \frac{R}{R_{0}} \biggr) ^{2}+\frac{2R}{R_{0}^{2}}, \\ & S_{X}=2 \omega_{1}+2 \omega_{2}+2 \biggl( \frac{R}{R_{0}} \biggr) ^{2}\omega_{2}+2 \biggl( \frac{R}{R_{0}} \biggr) ^{2}\omega_{3}, \\ & S_{Z}=2 \omega_{1}\frac{R}{R_{0}}+4 \omega_{2}\frac{R}{R_{0}}+2 \omega_{3}\frac{R}{R_{0}}. \end{aligned}$$

Appendix B: Calculus of Circulation Integral (48)

For the first component of the Piola-Kirchhoff stress vector, (48) provides ($\gamma =1$)

$$\begin{aligned} &\int_{-\frac{H}{2}}^{\frac{H}{2}}\hat{S} \biggl(\frac{B}{2}, Y \biggr) \cos \frac{B}{2r} dY+ \int_{-\frac{H}{2}}^{\frac{H}{2}}\hat{S} \biggl(- \frac{B}{2}, Y \biggr) \cos \biggl(-\frac{B}{2r} \biggr) dY \\ &\quad {}+ \int_{-\frac{B}{2}}^{ \frac{B}{2}}\hat{S} \biggl(X, -\frac{H}{2} \biggr) \sin \frac{X}{r} dX+ \int_{-\frac{B}{2}}^{\frac{B}{2}}\hat{S} \biggl(X, \frac{H}{2} \biggr) \sin \frac{X}{r} dX=0, \end{aligned}$$

(80)

where $(\lambda =\lambda_{X}=\lambda_{Y})$

$$ S=\hat{S}(X, Y)=2a \lambda +2b \lambda^{3}+2b \lambda \lambda_{Z} ^{2}+2c \lambda^{3} \lambda_{Z}^{2}-\frac{d}{\lambda }. $$

The calculus of the first integral gives

$$\begin{aligned} &\int_{-\frac{H}{2}}^{\frac{H}{2}}\hat{S} \biggl(\frac{B}{2}, Y \biggr) \cos \frac{B}{2r} dY \\ &\quad =2r \cos \frac{B}{2r}\biggl[2a e^{-\frac{QN}{r}} \sinh \frac{H}{2r}+\frac{2b}{3} e^{-\frac{3QN}{r}} \sinh \frac{3H}{2r}+ 2b \biggl[ \biggl( \frac{R+r}{R_{0}} \biggr) ^{2}e^{-\frac{QN}{r}}\sinh \frac{H}{2r} \\ &\quad \quad {}-\frac{r ( R+r ) }{R_{0}^{2}} e^{-\frac{2QN}{r}} \sinh \frac{H}{r} \cos \frac{B}{2r}+ \frac{1}{3} \biggl( \frac{r}{R_{0}} \biggr) ^{2}e^{-\frac{3QN}{r}} \sinh \frac{3H}{2r} \cos^{2}\frac{B}{2r}\biggr] \\ &\quad \quad {}+2c \biggl[ \frac{1}{3} \biggl( \frac{R+r}{R _{0}} \biggr) ^{2}e^{-\frac{3QN}{r}} \sinh \frac{3H}{2r} -\frac{r}{2}\frac{ ( R+r ) }{R_{0}^{2}} e^{-\frac{4QN}{r}} \sinh \frac{4H}{2r} \cos \frac{B}{2r} \\ &\quad \quad {}+ \frac{1}{5} \biggl( \frac{r}{R _{0}} \biggr) ^{2}e^{-\frac{5QN}{r}} \sinh \frac{5H}{2r} \cos^{2} \frac{B}{2r}\biggr] - d e^{\frac{QN}{r}}\sinh \frac{H}{2r}\biggr]. \end{aligned}$$

(81)

The second integral of (80) provides the same result (81) of the first integral, whereas the third and fourth integral of (80) are null. Therefore, to satisfy condition (48) with $\gamma =1$, it must be annulled the expression (81), which, however, does not have a simple form. To simplify (81), it can observed that the parameter $QN$ is numerically small and even smaller is the ratio $QN/r$ $(QN/r\ll 1)$. Furthermore, also the ratio $H/r$ is small. Therefore, setting $e^{\frac{QN}{r}}\simeq 1$ and approximating the hyperbolic sine with its argument ($\sinh x\simeq x$), (81) provides the following relationship among the radii of the kinematic model:²⁷

$$ R_{0}-R=r \biggl( 1-\cos \frac{B}{2r} \biggr) . $$

For the second component of the Piola-Kirchhoff stress vector, (48) provides ($\gamma =2$)

$$\begin{aligned} & \int_{-\frac{H}{2}}^{\frac{H}{2}}\hat{S} \biggl(\frac{B}{2}, Y \biggr) \sin \frac{B}{2r} dY+ \int_{-\frac{H}{2}}^{\frac{H}{2}}\hat{S} \biggl(- \frac{B}{2}, Y \biggr) \sin \biggl(-\frac{B}{2r} \biggr) dY \\ &\quad {} - \int_{-\frac{B}{2}}^{\frac{B}{2}}\hat{S} \biggl(X, -\frac{H}{2} \biggr) \cos \frac{X}{r} dX- \int_{-\frac{B}{2}}^{\frac{B}{2}}\hat{S} \biggl(X, \frac{H}{2} \biggr) \cos \frac{X}{r} dX=0. \end{aligned}$$

(82)

With the previous positions, (49) annuls the first and the second integral of (82). The calculus of the third integral gives

$$\begin{aligned} &\int_{-\frac{B}{2}}^{\frac{B}{2}}\hat{S} \biggl(X, -\frac{H}{2} \biggr) \cos \frac{X}{r} dX \\ &\quad =2a e^{-\frac{1}{r}(-\frac{H}{2}+QN)} 2r \sin \frac{B}{2r}+2b e^{-\frac{3}{r}(-\frac{H}{2}+QN)} 2r \sin \frac{B}{2r} \\ &\quad\quad {} + 2b \biggl[ \biggl( \frac{R+r}{R_{0}} \biggr) ^{2} e^{-\frac{1}{r}(-\frac{H}{2}+QN)} 2r \sin \frac{B}{2r}-2\frac{r(R+r)}{R_{0}^{2}} e^{-\frac{2}{r}(- \frac{H}{2}+QN)} r \\ &\quad\quad {} \times \biggl( \sin \frac{B}{2r} \cos \frac{B}{2r}+ \frac{B}{2r} \biggr) + \biggl( \frac{r}{R_{0}} \biggr) ^{2}e^{-\frac{3}{r}(-\frac{H}{2}+QN)} 2r \biggl( \sin \frac{B}{2r}-\frac{1}{3}\sin^{3} \frac{B}{2r} \biggr) \biggr] \\ &\quad\quad {} +2c \biggl[ \biggl( \frac{R+r}{R_{0}} \biggr) ^{2} e^{-\frac{3}{r}(-\frac{H}{2}+QN)} 2r \sin \frac{B}{2r} -2\frac{r(R+r)}{R_{0}^{2}} e^{-\frac{4}{r}(-\frac{H}{2}+QN)} r \\ &\quad\quad {} \times \biggl( \sin \frac{B}{2r} \cos \frac{B}{2r}+ \frac{B}{2r} \biggr) + \biggl( \frac{r}{R _{0}} \biggr) ^{2}e^{-\frac{5}{r}(-\frac{H}{2}+QN)} 2r \biggl( \sin \frac{B}{2r}- \frac{1}{3}\sin^{3}\frac{B}{2r} \biggr) \biggr] \\ &\quad\quad {} -d e^{\frac{1}{r}(-\frac{H}{2}+QN)} 2r \sin \frac{B}{2r}. \end{aligned}$$

(83)

The fourth integral is equal to the third one provided that the exponent $(-H/2)$ is replaced with $(H/2)$. Adding up the results of the third and fourth integral, setting $e^{\frac{QN}{r}}\simeq 1$ and approximating the hyperbolic cosine with unity, the following expression is obtained:

$$\begin{aligned} \mathit{Int} =&4ar \sin \frac{B}{2r}+4br \sin \frac{B}{2r}+4b \biggl[ \biggl( \frac{R+r}{R _{0}} \biggr) ^{2}r \sin \frac{B}{2r} \\ &{}- \frac{r(R+r)}{R_{0}^{2}} r \biggl( \sin \frac{B}{2r} \cos \frac{B}{2r}+ \frac{B}{2r} \biggr) + \biggl( \frac{r}{R_{0}} \biggr) ^{2}r \biggl( \sin \frac{B}{2r}-\frac{1}{3} \sin^{3}\frac{B}{2r} \biggr) \biggr] \\ &{}+4c \biggl[ \biggl( \frac{R+r}{R_{0}} \biggr) ^{2}r \sin \frac{B}{2r}- \frac{r(R+r)}{R_{0}^{2}} r \biggl( \sin \frac{B}{2r} \cos \frac{B}{2r}+ \frac{B}{2r} \biggr) \\ &{}+ \biggl( \frac{r}{R_{0}} \biggr) ^{2}r \biggl( \sin \frac{B}{2r}- \frac{1}{3}\sin^{3} \frac{B}{2r} \biggr) \biggr]-2dr \sin \frac{B}{2r}. \end{aligned}$$

(84)

This expression can be rearranged by using expression (49), however it does not completely vanish but it exhibits some residual terms,

$$ \mathit{Int}=4 ( a+b ) \biggl( \frac{r}{R_{0}} \biggr) ^{2} \biggl[ ( R+r ) \biggl( \sin \frac{B}{2r} \cos \frac{B}{2r}-\frac{B}{2r} \biggr) + \frac{2}{3}r \sin^{3}\frac{B}{2r} \biggr] , $$

(85)

that become numerically negligible as $B$ decreases with respect to $r$.

Essentially with this last remark also the boundary conditions can be considered fulfilled, of course on average over the whole boundary and with some numerical approximations. In any case, the procedure followed has allowed to obtain the formula (49), which has a simple and compact form, despite the complexity of the problem studied.