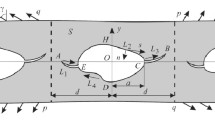
Abstract
An exact expression is derived for a path independent integral surrounding an elliptical hole in an infinite plate with tensile tractions at infinity for plane stress loading conditions. The plate is composed of a non-work-hardening material satisfying the Tresca yield condition under proportional loading and small strain assumptions. This problem may serve as a simple classroom example for the derivation of a relationship between crack opening displacement and path independent integral for a nonlinear elastic material satisfying the Tresca yield condition.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Cherepanov, G.P.: Crack propagation in continuous media. Prikl. Mat. Meh. 31, 476–488 (1967) (in Russian)
Cherepanov, G.P.: Mechanics of Brittle Fracture. McGraw-Hill, New York (1979)
Dugdale, D.S.: Yielding of steel sheets containing slits. J. Mech. Phys. Solids 8, 100–104 (1960)
Hutchinson, J.W.: Singular behavior at the end of a tensile crack in a hardening material. J. Mech. Phys. Solids 16, 13–31 (1968)
Hutchinson, J.W.: Plastic stress and strain fields at a crack tip. J. Mech. Phys. Solids 16, 337–347 (1968)
Griffith, A.A.: The phenomena of rupture and flow in solids. Trans. R. Soc. Lond. A 221, 163–198 (1920)
Inglis, C.E.: Stresses in a plate due to the presence of cracks and sharp notches. Trans. Inst. Naval Architects 55, 219–241 (1913)
Ivlev, D.D., Ershov, L.V.: Perturbation Method in the Theory of an Elastic–Plastic Body, pp. 160–170. “Nauka,” Glav. red. fiziko-matematicheskoi lit-ry, Moscow (1978) (in Russian)
Lawrence, J.D.: A Catalog of Special Plane Curves, pp. 42–43. Dover, Mineola, NY (1972)
Kachanov, L.M.: Fundamentals of the Theory of Elasticity. Dover, Mineola NY (2004)
Kharchenko, A.P.: Deformation in the vicinity of an elliptical hole in an elastic–plastic solid. Prikl. Meh. (Kiev) 10, 48–55 (1974) (in Russian)
Malvern, L.E.: Introduction to the Mechanics of a Continuous Medium, pp. 510–511. Prentice-Hall, Englewood Cliffs, NJ (1969)
Perlin, P.I.: Approximate method of solution of elastic–plastic problems. Inzhenernyi Sbornik 28, 145–150 (1960) (in Russian)
Rice, J.R.: A path independent integral and the approximate analysis of strain concentrations by notches and cracks. J. Appl. Mech. 35, 379–386 (1968)
Rice, J.R., Rosengren, G.F.: Plane strain deformation near a crack tip in a power-law hardening material. J. Mech. Phys. Solids 16, 1–12 (1968)
Rice, J.R.: Mathematical analysis in the mechanics of fracture. In: Liebowitz, H. (ed.) Fracture: An Advanced Treatise, vol 2, pp. 191–311. Academic, New York (1968)
Sokolnikoff, I.S.: Mathematical Theory of Elasticity. McGraw-Hill, New York (1956)
Sokolovskii, V.V.: Theory of Plasticity, 3rd edn. pp. 228–237. Vyssh. shkola, Moscow (1969) (in Russian)
Timoshenko, S.P.: Theory of Elasticity, 3rd edn. McGraw-Hill, New York (1970)
Unger, D.J.: Analytical Fracture Mechanics. Dover, Mineola, NY (2001)
Unger, D.J.: Perfectly plastic caustics for the opening mode of fracture. Theor. Appl. Fract. Mech. 44, 82–94 (2005)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Unger, D.J. Path Independent Integral for an Elliptical Hole in a Plate under Tension for Plane Stress Deformation Theory. J Elasticity 92, 217–226 (2008). https://doi.org/10.1007/s10659-008-9159-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-008-9159-z