Abstract
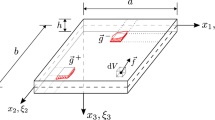
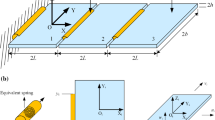
We present a deduction of the Kirchhoff–Love and Reissner–Mindlin kinematics of a simply-connected plate by using the formal asymptotic development method applied to the compatibility conditions of Saint-Venant and the formula of Cesàro–Volterra. This formal deduction is purely geometrical because we do not use any information coming from the loading or the constitutive behavior.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Amrouche, C., Ciarlet, P.G., Gratie, L., Kesavan, S.: On the characterizations of matrix fields as linearized strain tensor fields. J. Math. Pures Appl. 86, 116–132 (2006)
Cesàro, E.: Sulle formole del Volterra, fondamentali nella teoria delle distorsioni elastiche. Rend. Napoli Serie, Anno XLV 7(3a), 311–321 (1906)
Ciarlet, P.G.: Mathematical Elasticity, vol. II: Theory of Plates, Studies in Mathematics and its Applications. North-Holland, Amsterdam (1997)
Ciarlet, P.G., Ciarlet, P. Jr.: Another approach to linearized elasticity and a new proof of Korn’s inequality. Math. Models Methods Appl. Sci. 15, 259–271 (2005)
Fosdick, R., Royer-Carfagni, G.: A Stokes theorem for second-order tensor fields and its implications in continuum mechanics. Int. J. Non-Linear Mech. 40, 381–386 (2005)
Geymonat, G., Krasucki, F.: Some remarks on the compatibilty conditions in elasticity. Rend. Accad. Naz. Sci. XL 123, 175–182 (2005)
Geymonat, G., Krasucki, F.: Beltrami’s solutions of general equilibrium equations in continuum mechanics. C. R. Acad. Sci. Paris Série I 342, 359–363 (2006)
Gurtin, M.E.: The linear theory of elasticity. In: Truesdell, C. (ed.) Encyclopedia of Physics, vol. VIa/2. Springer, Berlin Heidelberg New York (1972)
Miara B., Podio-Guidugli, P.: Deduction by scaling: a unified approach to classical plate and rod theories. Asymptot. Anal. 51, 113–131 (2007)
Moreau, J.J.: Duality characterization of strain tensor distributions in arbitrary open set. J. Math. Anal. Appl. 72, 760–770 (1979)
Müller, S.: Paper presented at the course, classical and advanced theories of thin structures: mechanical and mathematical aspects. CISM, Udine, 5–9 June 2006
Paroni, R., Podio-Guidugli, P., Tomassetti, G.: A justification of the Reissner–Mindlin plate theory through variational convergence. Anal. Appl. 5, 165–182 (2007)
Podio-Guidugli, P.: An exact derivation of the thin plate equation. J. Elast. 22, 121-133 (1989)
Ting, T.W.: St. Venant’s compatibility conditions. Tensor 28, 5–12 (1974)
Volterra, V.: Sur l’équilibre des corps élastiques multiplement connexes. Ann. Sci. Ec. Norm. Super. 3ème Série 24, 401–517 (1907)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Geymonat, G., Krasucki, F. & Serpilli, M. The Kinematics of Plate Models: A Geometrical Deduction. J Elasticity 88, 299–309 (2007). https://doi.org/10.1007/s10659-007-9133-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-007-9133-1