Skip to main content
SpringerLink
Log in

Modeling oil dispersion under breaking waves. Part I: Wave hydrodynamics

  • Original Article
  • Published:
Environmental Fluid Mechanics Aims and scope Submit manuscript

Abstract

The dispersion (transport and breakup) of oil droplets under breaking waves is essential for evaluating the impact of oil spills on the environment, and for designing countermeasures. In this part of the work (Part I), the hydrodynamics of a wave breaker in a 1.0 m deep tank obtained experimentally by Rapp and Melville (Philos Trans R Soc Lond A Math Phys Eng Sci 331(1622):735–800, 1990) using the dispersive focusing method was investigated numerically using Reynold-averaged Navier–Stokes (RANS) within the CFD code ANSYS Fluent. The renormalization group (RNG) k–ε turbulence closure model was adopted to simulate wave turbulence, and the transient water–air interface was captured using volume of fluid (VOF) method. The simulated surface excursion and velocity fields matched closely the experimental observations during wave breaking. The energy dissipation of the wave crest showed good agreement with recent laboratory work and numerical simulations through evaluating the breaking parameter. The RANS approach was able to reproduce the turbulent kinetic energy field engendered by the breakers and simulated the residual turbulence within about two wave periods after the passage of the wave train. The VOF scheme Compressive provided a better agreement with the observation than the Geo-reconstruct scheme. The approach herein suggests that RANS method coupled with VOF in ANSYS Fluent is capable of capturing the major hydrodynamic forces and turbulence, and thus could be used to predict environmental processes within the breaking waves such as oil droplet formation and transport.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Alagan Chella M, Bihs H, Myrhaug D, Muskulus M (2016) Hydrodynamic characteristics and geometric properties of plunging and spilling breakers over impermeable slopes. Ocean Model 103:53–72

    Google Scholar 

  2. ANSYS (2013). ANSYS FLUENT Theory Guide 15.0

  3. Brackbill JU, Kothe DB, Zemach C (1992) A continuum method for modeling surface tension. J Comput Phys 100(2):335–354

    Google Scholar 

  4. Bradford SF (2000) Numerical simulation of surf zone dynamics. J Waterway Port Coast Ocean Eng 126(1):1–13

    Google Scholar 

  5. Brocchini M (2002) Free surface boundary conditions at a bubbly/weakly splashing air–water interface. Phys Fluids 14(6):1834–1840

    Google Scholar 

  6. Brown SA, Greaves DM, Magar V, Conley DC (2016) Evaluation of turbulence closure models under spilling and plunging breakers in the surf zone. Coast Eng 114:177–193

    Google Scholar 

  7. Chang K-A, Liu PL-F (1999) Experimental investigation of turbulence generated by breaking waves in water of intermediate depth. Phys Fluids 11(11):3390–3400

    Google Scholar 

  8. Chen G, Kharif C, Zaleski S, Li J (1999) Two-dimensional Navier–Stokes simulation of breaking waves. Phys Fluids 11(1):121–133

    Google Scholar 

  9. Cui F, Boufadel MC, Geng X, Gao F, Zhao L, King T, Lee K (2018) Oil droplets transport under a deep-water plunging breaker: impact of droplet inertia. J Geophys Res Oceans 123:9082–9100

    Google Scholar 

  10. De Padova D, Ben Meftah M, De Serio F, Mossa M, Sibilla S (2019) Characteristics of breaking vorticity in spilling and plunging waves investigated numerically by SPH. Environ Fluid Mech 20:233–260

    Google Scholar 

  11. Dean RG, Dalrymple RA (1991) Water wave mechanics for engineers and scientists. World Scientific Publishing Co Inc, Singapore

    Google Scholar 

  12. Deane GB, Stokes MD (2002) Scale dependence of bubble creation mechanisms in breaking waves. Nature 418(6900):839–844

    Google Scholar 

  13. Deike L, Melville WK, Popinet S (2016) Air entrainment and bubble statistics in breaking waves. J Fluid Mech 801:91–129

    Google Scholar 

  14. Deike L, Pizzo N, Melville WK (2017) Lagrangian transport by breaking surface waves. J Fluid Mech 829:364–391

    Google Scholar 

  15. Deike L, Popinet S, Melville WK (2015) Capillary effects on wave breaking. J Fluid Mech 769:541–569

    Google Scholar 

  16. Derakhti M, Kirby JT (2014) Bubble entrainment and liquid–bubble interaction under unsteady breaking waves. J Fluid Mech 761:464–506

    Google Scholar 

  17. Derakhti M, Kirby JT (2016) Breaking-onset, energy and momentum flux in unsteady focused wave packets. J Fluid Mech 790:553–581

    Google Scholar 

  18. Derakhti M, Kirby JT, Shi F, Ma G (2016) Wave breaking in the surf zone and deep-water in a non-hydrostatic RANS model. Part 1: organized wave motions. Ocean Model 107:125–138

    Google Scholar 

  19. Devolder B, Rauwoens P, Troch P (2017) Application of a buoyancy-modified k-ω SST turbulence model to simulate wave run-up around a monopile subjected to regular waves using OpenFOAM®. Coast Eng 125:81–94

    Google Scholar 

  20. Devolder B, Troch P, Rauwoens P (2018) Performance of a buoyancy-modified k–ω and k–ω SST turbulence model for simulating wave breaking under regular waves using OpenFOAM®. Coast Eng 138:49–65

    Google Scholar 

  21. Drazen DA, Melville WK (2009) Turbulence and mixing in unsteady breaking surface waves. J Fluid Mech 628:85–119

    Google Scholar 

  22. Drazen DA, Melville WK, Lenain LUC (2008) Inertial scaling of dissipation in unsteady breaking waves. J Fluid Mech 611:307–332

    Google Scholar 

  23. Duncan JH, Longuet-Higgins MS (1981) An experimental investigation of breaking waves produced by a towed hydrofoil. Proc R Soc Lond A Math Phys Sci 377(1770):331–348

    Google Scholar 

  24. Elliott AJ (1986) Shear diffusion and the spread of oil in the surface layers of the North Sea. Dtsch Hydrogr Z 39(3):113–137

    Google Scholar 

  25. Grare L, Peirson WL, Branger H, Walker JW, Giovanangeli J-P, Makin V (2013) Growth and dissipation of wind-forced, deep-water waves. J Fluid Mech 722:5–50

    Google Scholar 

  26. Iafrati A (2009) Numerical study of the effects of the breaking intensity on wave breaking flows. J Fluid Mech 622:371–411

    Google Scholar 

  27. Iafrati A (2011) Energy dissipation mechanisms in wave breaking processes: spilling and highly aerated plunging breaking events. J Geophys Res Oceans 116(C07024)

  28. Iafrati A, Campana EF (2005) Free-surface fluctuations behind microbreakers: space–time behaviour and subsurface flow field. J Fluid Mech 529:311–347

    Google Scholar 

  29. Kamath A, Alagan Chella M, Bihs H, Arntsen ØA (2016) Breaking wave interaction with a vertical cylinder and the effect of breaker location. Ocean Eng 128:105–115

    Google Scholar 

  30. Lakehal D, Liovic P (2011) Turbulence structure and interaction with steep breaking waves. J Fluid Mech 674:522–577

    Google Scholar 

  31. Larsen BE, Fuhrman DR (2018) On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier–Stokes models. J Fluid Mech 853:419–460

    Google Scholar 

  32. Li C, Miller J, Wang J, Koley S, Katz J (2017) Size distribution and dispersion of droplets generated by impingement of breaking waves on oil slicks. J Geophys Res Oceans 122(10):7938–7957

    Google Scholar 

  33. Li Z, Lee K, King T, Boufadel MC, Venosa AD (2009) Evaluating chemical dispersant efficacy in an experimental wave tank: 1—Dispersant effectiveness as function of the energy dissipation rate. Environ Eng Sci 26(6):1139–1148

    Google Scholar 

  34. Lim H-J, Chang K-A, Huang Z-C, Na B (2015) Experimental study on plunging breaking waves in deep water. J Geophys Res Oceans 120(3):2007–2049

    Google Scholar 

  35. Lin M-Y, Moeng C-H, Tsai W-T, Sullivan PP, Belcher SE (2008) Direct numerical simulation of wind-wave generation processes. J Fluid Mech 616:1–30

    Google Scholar 

  36. Longuet-Higgins MS (1988) Mechanisms of wave breaking in deep water. In: Kerman BR (ed) Sea surface sound: natural mechanisms of surface generated noise in the ocean. Springer, Dordrecht, pp 1–30

    Google Scholar 

  37. Longuet-Higgins MS (1998) Vorticity and curvature at a free surface. J Fluid Mech 356:149–153

    Google Scholar 

  38. Longuett-Higgins MS, Cokelet ED (1976) The deformation of steep surface waves on water I. A numerical method of computation. Proc R Soc Lond A 350:1–26

    Google Scholar 

  39. Lubin P, Glockner S (2015) Numerical simulations of three-dimensional plunging breaking waves: generation and evolution of aerated vortex filaments. J Fluid Mech 767:364–393

    Google Scholar 

  40. Lubin P, Vincent S, Abadie S, Caltagirone J-P (2006) Three-dimensional large eddy simulation of air entrainment under plunging breaking waves. Coast Eng 53(8):631–655

    Google Scholar 

  41. Lupieri G, Contento G (2015) Numerical simulations of 2-D steady and unsteady breaking waves. Ocean Eng 106:298–316

    Google Scholar 

  42. Ma G, Shi F, Kirby JT (2011) A polydisperse two-fluid model for surf zone bubble simulation. J Geophys Res Oceans 116(C05010)

  43. Melville WK (1994) Energy dissipation by breaking waves. Oceanograph Lit Rev 24(10):2041–2049

    Google Scholar 

  44. Melville WK, Veron F, White CJ (2002) The velocity field under breaking waves: coherent structures and turbulence. J Fluid Mech 454:203–233

    Google Scholar 

  45. Menter FR (1994) Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J 32(8):1598–1605

    Google Scholar 

  46. Noh WF, Woodward P (1976) SLIC (Simple Line Interface Calculation). In: van de Vooren AI, Zandbergen PJ (eds) Proceedings of the fifth international conference on numerical methods in fluid dynamics 28 June–July 2 1976 Twente University, Enschede. Springer, Berlin, pp 330–340

  47. Perlin M, He J, Bernal LP (1996) An experimental study of deep water plunging breakers. Phys Fluids 8(9):2365–2374

    Google Scholar 

  48. Phillips OM (1985) Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J Fluid Mech 156:505–531

    Google Scholar 

  49. Pizzo NE, Melville WK (2013) Vortex generation by deep-water breaking waves. J Fluid Mech 734:198–218

    Google Scholar 

  50. Pizzo NE, Melville WK (2016) Wave modulation: the geometry, kinematics, and dynamics of surface-wave packets. J Fluid Mech 803:292–312

    Google Scholar 

  51. Rapp RJ, Melville W (1990) Laboratory measurements of deep-water breaking waves. Philos Trans R Soc Lond A Math Phys Eng Sci 331(1622):735–800

    Google Scholar 

  52. Romero L, Melville WK, Kleiss JM (2012) Spectral energy dissipation due to surface wave breaking. J Phys Oceanogr 42(9):1421–1444

    Google Scholar 

  53. Sullivan PP, McWilliams JC, Melville WK (2007) Surface gravity wave effects in the oceanic boundary layer: large-eddy simulation with vortex force and stochastic breakers. J Fluid Mech 593:405–452

    Google Scholar 

  54. Tanaka M (2001) A method of studying nonlinear random field of surface gravity waves by direct numerical simulation. Fluid Dyn Res 28(1):41–60

    Google Scholar 

  55. Tian Z, Perlin M, Choi W (2010) Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model. J Fluid Mech 655:217–257

    Google Scholar 

  56. Tian Z, Perlin M, Choi W (2012) An eddy viscosity model for two-dimensional breaking waves and its validation with laboratory experiments. Phys Fluids 24(3):036601

    Google Scholar 

  57. Ting FCK, Kirby JT (1994) Observation of undertow and turbulence in a laboratory surf zone. Coast Eng 24(1):51–80

    Google Scholar 

  58. Ubbink O (1997). Numerical prediction of two fluid systems with sharp interfaces. Doctor of Philosophy, Imperial College of Science, Technology and Medicine

  59. Wilcox DC (2008) Formulation of the k-w turbulence model revisited. AIAA J 46(11):2823–2838

    Google Scholar 

  60. Xie Z (2013) Two-phase flow modelling of spilling and plunging breaking waves. Appl Math Model 37(6):3698–3713

    Google Scholar 

  61. Yakhot V, Orszag S, Thangam S, Gatski T, Speziale C (1992) Development of turbulence models for shear flows by a double expansion technique. Phys Fluids A 4(7):1510–1520

    Google Scholar 

  62. Yakhot V, Orszag SA (1986) Renormalization group analysis of turbulence. I. Basic theory. J Sci Comput 1(1):3–51

    Google Scholar 

  63. Youngs D (1982) Time-dependent multi-material flow with large fluid distortion. Numer Methods Fluid Dyn 24:273–285

    Google Scholar 

  64. Zhao L, Torlapati J, Boufadel MC, King T, Robinson B, Lee K (2014) VDROP: a comprehensive model for droplet formation of oils and gases in liquids-Incorporation of the interfacial tension and droplet viscosity. Chem Eng J 253:93–106

    Google Scholar 

  65. Zhao Q, Tanimoto K (1999) Numerical simulation of breaking waves by large eddy simulation and VOF method. Coast Eng 1998:892–905

    Google Scholar 

  66. Zheyu Z, Tian-Jian H, Daniel C, Xiaofeng L (2017) Large-eddy simulation of wave-breaking induced turbulent coherent structures and suspended sediment transport on a barred beach. J Geophys Res Oceans 122(1):207–235

    Google Scholar 

  67. Zhou Z, Sangermano J, Hsu T-J, Ting FCK (2014) A numerical investigation of wave-breaking-induced turbulent coherent structure under a solitary wave. J Geophys Res Oceans 119(10):6952–6973

    Google Scholar 

Download references

Acknowledgements

This research was supported by a contract with the Department of Fisheries and Oceans Canada, Center for Offshore Oil and Gas Exploration Research, and through a grant from the Multi-Partner Research Initiative under Grant Number MECTS-#3939073-v1-OFSCP. However, no official endorsement should be implied by these entities. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (NSF) Grant Number TG-BCS190002. Specifically, we used the Bridges computer cluster, which is an NSF-funded system at the Pittsburgh Supercomputing Center (PSC).

Author information

Authors and Affiliations

  1. Center for Natural Resources, Civil and Environmental Engineering Department, New Jersey Institute of Technology, Newark, NJ, USA

    Fangda Cui, Cosan Daskiran & Michel C. Boufadel

  2. Department of Fisheries and Oceans, Dartmouth, NS, Canada

    Thomas King, Brian Robinson & Kenneth Lee

  3. Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD, USA

    Joseph Katz

Authors
  1. Fangda Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Cosan Daskiran
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thomas King
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Brian Robinson
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Kenneth Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Joseph Katz
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Michel C. Boufadel
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michel C. Boufadel.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

See Table 3 and Fig. 16.

Table 3 Wavenumber and frequency of the wave packet with a constant wave amplitude an = 0.34 cm
Full size table
Fig. 16
figure 16

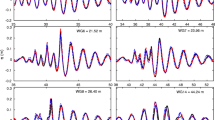
Time series of the horizontal velocity (left panel) and vertical velocity (right panel) at x = 0.0 m (inlet boundary) and z = 0.6 m (water level in the absence of waves). The vertical velocity is 90o degree out of phase with the horizontal velocity, so, for example, the vertical velocity is zero when the horizontal velocity is maximum

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cui, F., Daskiran, C., King, T. et al. Modeling oil dispersion under breaking waves. Part I: Wave hydrodynamics. Environ Fluid Mech 20, 1527–1551 (2020). https://doi.org/10.1007/s10652-020-09753-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10652-020-09753-7

Keywords

Search

Navigation