Waves and turbulence in katabatic winds

Abstract

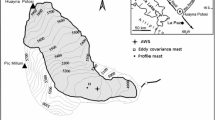
The measurements taken during the Vertical Transport and Mixing Experiment (VTMX, October, 2000) on a northeastern slope of Salt Lake Valley, Utah, were used to calculate the statistics of velocity fluctuations in a katabatic gravity current in the absence of synoptic forcing. The data from ultrasonic anemometer-thermometers placed at elevations 4.5 and 13.9 m were used. The contributions of small-scale turbulence and waves were isolated by applying a high-pass digital (Elliptical) filter, whereupon the filtered quantities were identified as small-scale turbulence and the rest as internal gravity waves. Internal waves were found to play a role not only at canonical large gradient Richardson numbers $(\overline{\hbox {Ri}_\mathrm{g} } >1)$, but sometimes at smaller values $(0.1 < \overline{\hbox {Ri}_\mathrm{g}}<1)$, in contrast to typical observations in flat-terrain stable boundary layers. This may be attributed, at least partly, to (critical) internal waves on the slope, identified by Princevac et al. [1], which degenerate into turbulence and help maintain an active internal wave field. The applicability of both Monin-Obukhov (MO) similarity theory and local scaling to filtered and unfiltered data was tested by analyzing rms velocity fluctuations as a function of the stability parameter z/L, where L is the Obukhov length and z the height above the ground. For weaker stabilities, $\hbox {z/L}<1$, the MO similarity and local scaling were valid for both filtered and unfiltered data. Conversely, when $\hbox {z/L}>1$, the use of both scaling types is questionable, although filtered data showed a tendency to follow local scaling. A relationship between z/L and $\overline{\hbox {Ri}_\mathrm{g} }$ was identified. Eddy diffusivities of momentum $\hbox {K}_\mathrm{M}$ and heat $\hbox {K}_\mathrm{H}$ were dependent on wave activities, notably when $\overline{\hbox {Ri}_\mathrm{g} } > 1$. The ratio $\hbox {K}_{\mathrm{H}}/\hbox {K}_{\mathrm{M}}$ dropped well below unity at high $\overline{\hbox {Ri}_\mathrm{g} }$, in consonance with previous laboratory stratified shear layer measurements as well as other field observations.