The flow of high-Reynolds axisymmetric gravity currents of a stratified fluid into a stratified ambient: shallow-water and box model solutions

Abstract

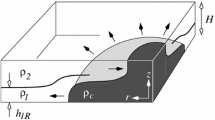
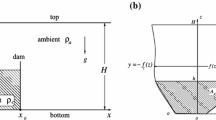
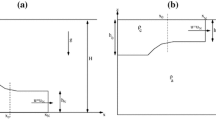
We consider the axisymmetric flow (in a full cylinder or a wedge) of high-Reynolds-number Boussinesq gravity currents and intrusions systems in which both the ambient and the propagating “current” are linearly stratified. The main focus is on a current of fixed volume released from a cylinder lock; the height ratio of the fluids H, and the stratification parameter of the ambient S, are quite general. We develop a one-layer shallow-water model. The internal stratification enters as a new dimensionless parameter, ${\sigma \in [0, 1]}$. In general, the time-dependent motion is obtained by standard finite-difference solutions; a self-similar analytical solution exists for S = 0. We show that, in general, the speed of propagation decreases when the internal stratification becomes more pronounced (σ increases). We also developed a box-model approximation, and show that the resulting radius of propagation is in good agreement with the more rigorous shallow-water prediction.