Abstract
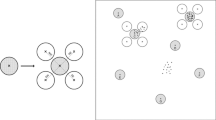
A probabilistic sampling approach for design-unbiased estimation of area-related quantitative characteristics of spatially dispersed population units is proposed. The developed field protocol includes a fixed number of 3 units per sampling location and is based on partial triangulations over their natural neighbors to derive the individual inclusion probabilities. The performance of the proposed design is tested in comparison to fixed area sample plots in a simulation with two forest stands. Evaluation is based on a general approach for areal sampling in which all characteristics of the resulting population of possible samples is derived analytically by means of a complete tessellation of the areal sampling frame. The example simulation shows promising results. Expected errors under this design are comparable to sample plots including a much greater number of trees per plot.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Affleck D, Gregoire T, Valentine H (2005) Design unbiased estimation in line intersect sampling using segmented transects. Environ Ecol Stat 12(2): 139–154
Aurenhammer F (1991) Voronoi diagrams–a survey of a fundamental geometric data structure. ACM Comput Surv 23(3): 345–405. doi:10.1145/116873.116880
Barabesi L (2001) A design-based approach to the estimation of plant density using point-to-plant sampling. J Agric Biol Environ Stat 6(1): 89–98
Barabesi L, Franceschi S (2010) Sampling properties of spatial total estimators under tessellation stratified designs. Environmetrics. doi:10.1002/env.1046
Batcheler CL (1971) Estimation of density from a sample of joint point and nearest-neighbor distances. Ecology 52(4): 703–709
Clark PJ, Evans FC (1954) Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology 35(4): 445–453
Cochran WG (1977) Sampling Techniques. Whiley, New York
Condit R (1998) Tropical Forest Census Plots. Springer and R. G. Landes Company, Berlin, Germany, and Georgetown, Texas
Cottam G, Curtis JT (1956) The use of distance measures in phytosociological sampling. Ecology 37(3): 451–460
Cox TF (1976) The robust estimation of the density of a forest stand using a new conditioned distance method. Biometrika 63(3): 493–499
Delincé J (1986) Robust density-estimation through distance measurements. Ecology 67(6): 1576–1581
Eberhardt LL (1967) Some developments in ‘distance sampling’. Biometrics 23: 207–216
Engeman RM, Sugihara RT, Pank LF, Dusenberry WE (1994) A comparison of plotless density estimators using monte carlo simulation. Ecology 75(6): 1769–1779
Engeman RM, Nielson RM, Sugihara RT (2005) Evaluation of optimized variable area transect sampling using totally enumerated field data sets. Environmetrics 16(7): 767–772
Errico D (1981) Some methods of sampling triangle based probability polygons for forestry applications. Master’s thesis, Department of forestry, University of British Columbia
Fraser A (1977) Triangle-based probability polygons for forest sampling. For Sci 23: 111–121
Gregoire T (1998) Design-based and model-based inference in survey sampling: appreciating the difference. Can J For Res 28(10): 1429–1447
Gregoire TG, Valentine HT (2008) Sampling strategies for natural resources and the environment. Applied environmental statistics. Chapman Hall/CRC, London
Halls PJ, Bulling M, White PCL, Garland L, Harris S (2001) Dirichlet neighbours: revisiting dirichlet tessellation for neighbourhood analysis. Comput Environ Urban Syst 25(1): 105–117. doi:10.1016/S0198-9715(00)00035-1
Hubbel S, Foster R, O’Brian S, Harms K, Condit R, Wechsler B, Wright S, de Lao L (1999) Light gap disturbance, recruitment limitation, and tree diversity in a neotropical forest. Science 283: 554–557
Kleinn C, Vilčko F (2006a) Design-unbiased estimation for point-to-tree distance sampling. Can J For Res 36: 1407–1414
Kleinn C, Vilčko F (2006b) A new empirical approach for estimation in k-tree sampling. For Ecol Manag 237: 522–533
Kronenfeld BJ (2009) A plotless density estimator based on the asymptotic limit of ordered distance estimation values. For Sci 55(4): 283–292
Law R, Illian J, Burslem D, Gratzer G, Gunatilleke CVS, Gunatilleke IAUN (2009) Ecological information from spatial patterns of plants: insights from point process theory. J Ecol 97: 616–628
Lessard VC, Drummer TD, Reed DD (2002) Precision of density estimates from fixed-radius plots compared to n-tree distance sampling. For Sci 48(1): 1–6
Lowell KE (1997) An empirical evaluation of spatially based forest inventory samples. Can J For Res 27: 352–360
Lynch T, Wittwer R (2003) n-Tree distance sampling for per-tree estimates with application to unequal-sized cluster sampling of increment core data. Can J For Res 33(7): 1189–1195. doi:10.1139/X03-036
Lynch TB, Rusydi R (1999) Distance sampling for forest inventory in indonesian teak plantations. For Ecol Manag 113: 215–221
Magnussen S, Kleinn C, Picard N (2008a) Two new density estimators for distance sampling. Eur J For Res 127(3): 213–224. doi:10.1007/s10342-007-0197-z
Magnussen S, Picard N, Kleinn C (2008b) A Gamma-Poisson distribution of point to k nearest event distance. For Sci 54(4): 429–441
Mandallaz D (1991) A unified approach to sampling theory for forest inventory based on infinite population models. Phd thesis, ETH Zürich
McIntire EJB, Fajardo A (2009) Beyond description: the active and effective way to infer processes from spatial patterns. Ecology 90(1): 46–56. doi:10.1890/07-2096.1
Nielson RM, Sugihara RT, Boardman TJ, Engeman RM (2004) Optimization of ordered distance sampling. Environmetrics 15(2): 119–128
Nothdurft A, Saborowski J, Nuske R, Stoyan D (2010) Density estimation based on k-tree sampling and point pattern reconstruction. Can J For Res 40: 953–967
Okabe A, Boots B, Sugihara K, Chiu SN (1999) Spatial tesselations. concepts and applications of voronoi diagrams. Wiley Series in Probability and Statistics. Wiley, New york
Payandeh B, Ek A (1986) Distance methods and density estimators. Can J For Res 16(5): 918–924
Picard N, Kouyate A, Dessard H (2005) Tree density estimations using a distance method in mali savanna. For Sci 51(1): 7–18
Prodan M (1968) Punktstichprobe für die Forsteinrichtung. Forst und Holzwirt 23(11): 225–226
Ripley BD (1977) Modelling spatial patterns. J Royal Stat Soc Ser B (Methodological) 39(2): 172–212
Roesch FA, Green EJ, Scott CT (1993) An alternative view of forest sampling. Surv Methodol 19(2): 199–204
Särndal CE, Swensson B, Wretman J (1992) Model assisted survey sampling. Springer, New York, p 694
Sibson R (1980) The dirichlet tessellation as an aid in data analysis. Scand J Stat 7(1): 14–20
Staupendahl K (2008) The modified six-tree-sample—a suitable method for forest stand assessment. Allgemeine Forst und Jagdzeitung 179(2–3): 21–33
Steinke I, Hennenberg K (2006) On the power of plotless density estimators for statistical comparisons of plant populations. Can J Bot 84(3): 421–432. doi:10.1139/B05-135
Thompson HR (1956) Distribution of distance to nth neighbor in a population of randomly distributed individuals. Ecology 37(2): 391–394
Ward D (1991) Triangular tesselation: a new approach to forest inventory. For Ecol Manag 44: 285–290
White N, Engeman R, Sugihara R, Krupa H (2008) A comparison of plotless density estimators using monte carlo simulation on totally enumerated field data sets. BMC Ecol 8(1): 6. doi:10.1186/1472-6785-8-6
Williams MS (2001) New approach to areal sampling in ecological surveys. For Ecol Manag 154: 11–22
Acknowledgments
This research was supported by the German Research Foundation DFG (KL 894/ 13-1). We thank Sebastian Schnell for helpful methodological and technical discussions. Further we thank two anonymous reviewers. Their extensive contributions to formulate the idea was substantial. We appreciated constructive comments, help and valuable suggestions to improve the manuscript.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Fehrmann, L., Gregoire, T.G. & Kleinn, C. Triangulation based inclusion probabilities: a design-unbiased sampling approach. Environ Ecol Stat 19, 107–123 (2012). https://doi.org/10.1007/s10651-011-0177-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10651-011-0177-9