Skip to main content
SpringerLink
Log in

Using Fast and Slow Processes to Manage Resources with Thresholds

  • Published:
Environmental and Resource Economics Aims and scope Submit manuscript

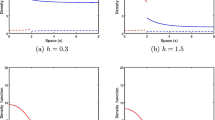
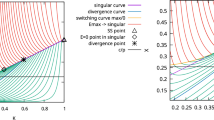
Abstract

Economists have relied on convexity assumptions for a long time but many natural resources that stem from ecosystems have non-convexities in their dynamics. This article illustrates the consequences of relaxing convexity assumptions for management and the role of fast and slow variables. The paper presents a general framework to handle systems with fast and slow variables, and illustrates the method using a model of coral reefs subject to fishing pressure. The insights obtained are used to discuss alternative management strategies.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Arrow K. J., Fisher A. C. (1974) Environmental Preservation Uncertainty, and Irreversibility. Quarterly Journal of Economics 88:312–319

    Article  Google Scholar 

  • Brock W. A., Starrett D. (2003) Managing Systems with Non-convex Positive Feedback. Environmental and Resource Economics 26(4):575–602

    Article  Google Scholar 

  • Carpenter S. R. (2003) Regime Shifts in Lake Ecosystems: Pattern and Variation, Vol 15, Excellence in Ecology Series. Ecology Institute, Oldendorf/Luhe, Germany

    Google Scholar 

  • Carpenter S. R., Brock W. A. (2004) Spatial Complexity, Resilience, and Policy Diversity: Fishing on Lake-rich Landscapes. Ecology and Society 9(1):1–31

    Google Scholar 

  • Carpenter S. R., Turner M. G. (2000a) Special Issue on Interactions of Fast and Slow Variables in Ecosystems. Ecosystems 3(6):495–595. Special issue

    Article  Google Scholar 

  • Carpenter S. R., Turner M. G. (2001) Hares and Tortoises: Interactions of Fast and Slow Variables in Ecosystems. Ecosystems 3(6):495–497

    Article  Google Scholar 

  • Clark, C. W. (1990), Mathematical Bioeconomics – The Optimal Management of Renewable Resources, in: Pure and Applied Mathematics, 2nd edition. Wiley. First published in 1976.

  • Claussen M., Kubatzki C., Brovkin V., Ganopolski A., Hoelzmann P., Pachur H. (1999) Simulation of an Abrupt Change in Saharan Vegetation at the End of Mid-Holocene. Geophysical Research Letters 26(14):2037–2040

    Article  Google Scholar 

  • Crépin, A.-S. (2002), Tackling the Economics of Ecosystems, PhD Thesis, Stockholm University, Department of Economics. Dissertations in Economics 2002, 6.

  • Crépin A.-S. (2003) Multiple Species Boreal Forests – What Faustmann Missed. Environmental and Resource Economics 26(4):625–646

    Article  Google Scholar 

  • Dasgupta, P. and K.-G. Mäler (2003), The Economics of Non-convex Environments. Environmental and Resource Economics 26(4), Special issue.

  • Epstein, L. S. (1980) Decision-making and the Temporal Resolution of Uncertainty. International Economic Review 21(2):269–284

    Article  Google Scholar 

  • Fenichel N. (1979) Geometric Singular Perturbation Theory for Ordinary Differential Equations. Journal of Differential Equations 31:53–98

    Article  Google Scholar 

  • Folke, C., S. Carpenter, T. Elmqvist, L. C. Gunderson, B. Walker, J. Bengtsson, F. Berkes, J.␣Colding, K. Danell, M. Falkenmark, L. Gordon, R. Kasperson, N. Kautsky, A. Kinzig, S. Levin, K.-G. Mäler, F. Moberg, L. Ohlsson, P. Olsson, E. Ostrom, W. Reid, J.␣Rockström, H. Savenise and U. Svedin (2002), Resilience and Sustainable Development: Building Adaptive Capacity in a World of Transformation, Edita Nordstedts Tryckeri AB, Stockholm. Scientific Background Paper on Resilience for the Process of The World Summit on Sustainable Development on Behalf of The Environmental Advisory Council to the Swedish Government.

  • Freixas, X. and J.-J. Laffont (1984), ‘On the Irreversibility Effect’, in M. Boyer and R.␣Kihlstrom, eds., Bayesian Models in Economic Theory. Elsevier, Dordrecht.

  • Gollier C. (2001) Should we beware of the precautionary principle?. Economic Policy 0(33):301–321

    Article  Google Scholar 

  • Groffman P. M., Baron J. S., Blett T., Gold A. J., Goodman I., Gunderson L. H., Levinson B. M., Palmer M. A., Paerl H. W., Peterson G. D., Poff N. L., Rejeski D. W., Reynolds J. F., Turner M. G., Weathers K. C., Wiens J. (2006) Ecological Thresholds: The Key to Succesful Environmental Management or an Important Concept with No Practical Application? Ecosystems 9(1):1–13

    Article  Google Scholar 

  • Henry C. (1974) Investment Decisions Under Uncertainty: The “Irreversibility Effeet”. American Economic Review 64(5):1006–1012

    Google Scholar 

  • Holling C. (1959) The Components of Predation as Revealed by a Study of Small Mammal Predation of the European Pine Sawfly. Canadian Entomologist 91:293–320

    Article  Google Scholar 

  • Holling, C.S. (ed) (1978), Adaptive Environmental Assessment and Management. New York: John Wiley and Sons

  • Immordino G. (2003) Looking for a Guide to Protect the Environment: The Development of the Precautionary Principle. Journal of Economic Surveys 17(5):629–643

    Article  Google Scholar 

  • Jennings S., Polunin N. (1997) Impacts of Predator Depletion by Fishing on the Biomass and Diversity of Non-target Reef Fish Communities. Coral Reefs 16:71–82

    Article  Google Scholar 

  • Knowler D., Barbier E. B. (2005) Managing the Black Sea Anchovy Fishery with Nutrient Enrichment and a Biological Invader. Marine Resource Economics 20(3):263–285

    Google Scholar 

  • Kokotovic P., Sannuti P. (1968) Singular Perturbation Methods for Reducing Model Order in Optimal Control Design. IEEE Transactions on Automatic Control 13(4):377–384

    Article  Google Scholar 

  • Krutilla, J. V., C. J. Cichetti, M. A. I. Freeman and C. S. Russell (1972), ‘Observations on the Economics of Irreplaceable Assets’, in A. V. Kneese and B. T. Bower, eds., Environmental Quality Analysis, Chapter 3, pp. 69–112. The Johns Hopkins Press. Papers from a Resources for the Future conference.

  • Kuznetsov, Y. A. (1995), ‘Elements of Applied Bifurcation Theory’, in Applied Mathematical Sciences, Vol. 112. Springer-Verlag.

  • Ludwig D., Carpenter S., Brock W. (2003) Optimal Phosphorus Loading for a Potentially Eutrophic Lake. Ecological Applications 13(4):1135–1152

    Google Scholar 

  • Ludwig D., Jones D. D., Holling C. S. (1978) Qualitative Analysis of Insect Outbreak Systems: The Spruce Budworm and the Forest. Journal of Animal Ecology 47:315–332

    Article  Google Scholar 

  • Mäler K.-G., Xepapadeas A., de Zeeuw A. (2003) The Economics of Shallow Lakes. Environmental and Resource Economics 26(4):603–624

    Article  Google Scholar 

  • Mäler, K.-G. and A. Fisher (2005), `Environment, Uncertainty and Option Values', Ch. 13 in K.G. Mäler and J. R. Vincent, eds., Handbook of Environmental Economics, Vol. 2. North-Holland

  • Margolis, M. B. and E. Naevdal (2004), Safe Minimum Standards in Dynamic Resource Problems—Conditions for Living on the Edge of Risk, RFF Discussion paper 04-03. Available at www.rff.org/rff/Documents/RFF-DP-04-03.pdf

  • McClanahan T. R., Bergman K., Huitric M., McField M., Elfwing T., Nyström M., Nordemar I. (2000) Response of Fishes to Algae Reduction on Glover Reef, Belize. Marine Ecology Progress Series 206:273–282

    Google Scholar 

  • Milik A., Prskawetz A., Feichtinger G., Sanderson W. C. (1996) Slow-fast Dynamics in Wonderland. Environmental Modeling and Assessment 1(1,2):3–17

    Google Scholar 

  • Naidu D. (2002) Singular Perturbations and Time Scales in Control Theory and Applications: An Overview. Dynamics of Continuous. Discrete and Impulsive Systems 9:233–278

    Article  Google Scholar 

  • Nyström M., Folke C., Moberg F. (2000) Coral Reef Disturbance and Resilience in a Human-dominated Environment. Trends in Ecology and Evolution 15(10):413–417

    Article  Google Scholar 

  • Perrings, C. (1991), ‘Reserved Rationality and the Precautionary Principle: Technological Change, Time and Uncertainty in Environemntal Decision Making’, in R. Costanza, ed., Ecological Economics – The Science and Management of Sustainability, Chapter 11, pp. 153–167. Columbia University Press.

  • Pontryagin, L., V. Boltyanskii, R. Gamkrelidze and E. Mishchenko (1964), The Mathematical Theory of Optimal Processes. Pergamon Press. Translated by D. E. Brown.

  • Real, L. (1977), `The Kinetics of Functional Response', American Naturalist, 111, 289–300

    Google Scholar 

  • Rinaldi S., Scheffer M. (2000) Geometric Analysis of Ecological Models with Slow and Fast Processes. Ecosystems 3(6):507–521

    Article  Google Scholar 

  • Roberts C. M. (1995) Effects of Fishing on the Ecosystem Structure of Coral Reefs. Conservation Biology 9(5):988–995

    Article  Google Scholar 

  • Scheffer M., Szabó S., Gragnani A., Van Nes E. H., Rinaldi S., Kautsky N., Norberg J., Roijackers R. M., Franken R. J. (2003) Floating Plant Dominance as a Stable State. Proceedings of the National Academy of Sciences of the United States of America 100(7):4040–4045

    Article  Google Scholar 

  • Segel L. A. (1972) Simplification and Scaling. SIAM Review 14(4):547–571

    Article  Google Scholar 

  • Stewart B., Jones G. (2001) Associations Between the Abundance of Piscivorous Fishes and Their Prey on Coral Reefs: Implications for Prey-fish Mortality. Marine Biology 138:383–397

    Article  Google Scholar 

  • Tikhonov A. (1952) Systems of Differential Equations Containing Small Parameters at Derivatives. Matematicheskii Sbornik 31:575–86. In Russian

    Google Scholar 

  • Turchin P. (2003) Complex Population Dynamics – A Theoretical/Empirical Analysis, Vol. 35, Monographs in Population Biology. Princeton University Press, Princeton/Oxford

    Google Scholar 

  • Ulph A., Ulph D. (1997) Global Warming, Irreversibility and Learning. Economic Journal 107(442):636–649

    Article  Google Scholar 

  • Wagener F. (2003) Skiba Points and Heteroclinic Bifurcation Points, with Applications to the Shallow Lake System. Journal of Economic Dynamics and Control 27(9):1533–1561

    Article  Google Scholar 

  • Walters, C. (1986), Adaptive Management of Renewable Resources. New York: MacMillan

  • Weisbrod B. A. (1964) Collective-consumption Services of Individual-consumption Goods. The Quarterly Journal of Economics 78(3):471–477

    Article  Google Scholar 

Download references

Acknowledgments

Thanks to Claire Armstrong, Stephen Carpenter, Miriam Huitric, Karl-Göran␣Mäler, David Starrett, Anastasios Xepapadeas, and to two anonymous referees for their useful comments on the paper. Grants from FORMAS are gratefully acknowledged.

Author information

Authors and Affiliations

  1. The Beijer International Institute of Ecological Economics, The Royal Swedish Academy of Sciences, Box 50005, 10405, Stockholm, Sweden

    Anne-Sophie Crépin

Authors
  1. Anne-Sophie Crépin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anne-Sophie Crépin.

Electronic supplementary material

Rights and permissions

Reprints and permissions

About this article

Cite this article

Crépin, AS. Using Fast and Slow Processes to Manage Resources with Thresholds. Environ Resource Econ 36, 191–213 (2007). https://doi.org/10.1007/s10640-006-9029-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10640-006-9029-8

Keywords

JEL classification

Search

Navigation