A neural network solution for forecasting labor demand of drop-in peer tutoring centers with long planning horizons

Abstract

Like many other service organizations, drop-in peer tutoring centers often struggle to determine the required number of qualified tutors necessary to meet learner expectations. Service work is largely a response to probabilistic calls for staff action and therefore difficult to forecast with precision. Moreover, forecasting models under long planning horizons often lack the complexity or specificity necessary to accurately predict flexible labor demand due to sparse availability of influential model inputs. This study builds upon the flexible demand literature by exploring the use of neural networks for labor demand forecasting for a drop-in peer tutoring center of a large university. Specifically, this study employs a neural network solution that includes a genetic algorithm to search for optimal solutions using evolutional processes. The proposed forecasting model outperforms traditional smoothing and extrapolation forecasting methods.

Appendix 1 – Technical overview of the NNSOA

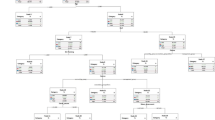
This section provides a technical overview of the Neural Network Simultaneous Optimization Algorithm (NNSOA) used in this study. The NNSOA first determines the appropriate number of hidden nodes for the neural network. Starting with two hidden nodes, the neural network is trained for 1000 generations and the best solution is saved. An additional hidden node is inserted into the best solution and trained for another 1000 generations. The best solution from the previous architecture is brought into the next architecture by setting the weights of the additional node to zero in order to preserve previous learning. The remaining solutions of the new neural network are reinitialized using a different random seed for drawing initial weights. The process of adding new hidden nodes and retraining continues until the new hidden node fails to improve overall performance. At this point the initial structure of the neural network is set.

It has been shown that a variety of neural network structures will reduce to the same equivalent structure (Dorsey et al. 1994a; Dorsey et al. 1994b). The NNSOA next follows the genetic algorithm logic as shown in Fig. 4 to determine the most parsimonious set of inputs for the model. It first builds a population of 12 solutions by modifying the input and output weights of the neural network. The input weights are randomly drawn from a uniform probability distribution [−1,1]. The output weights are determined by ordinary least squares, which prior research has found most effective and efficient (Dorsey et al. 1994a; Sexton et al. 1998; Sexton et al. 2003). These 12 solutions make up the first generation. The algorithm next creates a series of 10,000 successive populations, each a genetically modified version of the previous.

Fig. 4

NNSOA flowchart

At the beginning of each iteration all solutions of the current generation are individually evaluated by an objective function based on the sum of squares error (SSE). The function rewards parsimony by penalizing for each non-zero weight in the solution multiplied by the solution’s root mean square error (RMSE). The objective function is presented in eq. 3 below.

$$ E={\sum}_{i=1}^N{\left({O}_i-{\hat{O}}_i\right)}^2+C\sqrt{\frac{\sum_{i-1}^N{\left({O}_i-{\hat{O}}_i\right)}^2}{N}}. $$

(3)

where:

N:

the number of observations in the solution

O:

the observed value of the dependent variable

$\hat{O}$ :

the estimated value of the dependent variable

C:

the number of non-zero weights in the solution

The probability of a solution being redrawn in the next generation is determined by eq. 4. A next generation of 12 solutions is then randomly drawn with replacement from the current generation (i.e. reproduction). Duplication is allowed. Probabilities assigned in the evaluation step ensure that better solutions are more likely than poor solutions to appear in the next generation. In this way, traits that favor the objective function will reproduce and thrive in future generations, while weaker traits will die out over time.

$$ P(survival)=\frac{E_{max}-E}{\sum_{i=1}^{12}\left({E}_{max}-{E}_i\right)} $$

(4)

where:

E:

objective value of a given solution

E_max:

maximum objective value of the current population

The 12 solutions of the next generation are then randomly organized into mating pairs. A random number is drawn from a uniform distribution [−1,1] for each pair. Each weight in the mating pair that is numerically less than the random number is switched for the weight in the same position of the mating solution. This crossover creates two new solutions, each with some parameters (weights) from each parent solution. Finally, each weight in each of the 12 solutions may receive additional adjustment (i.e. mutation). Each weight has a 5% chance for replacement by a randomly drawn value from the entire weight space. Searching the entire weight space enhances the algorithm’s ability to find global solutions. After 70% of specified generations are processed, convergence is enhanced by varying each mutation by a small random amount. The size of the random amount decreases with each subsequent generation. Once the specified number of generations have processed (10,000 for this study) the best solution is selected from the last generation according to the same objective function of the evaluation step.