Skip to main content
SpringerLink
Log in

On the approximate solution of weakly singular integro-differential equations of Volterra type

  • Numerical Methods
  • Published:
Differential Equations Aims and scope Submit manuscript

Abstract

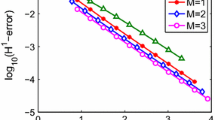
Recently, the convergence rate of the collocation method for integral and integro-differential equations with weakly singular kernels has been studied in a series of papers [1–7]. The present paper belongs to the same series. We analyze the possibility of constructing approximate solutions of high-order accuracy on a uniform or almost uniform grid for weakly singular integro-differential equations of Volterra type.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. A.A. Pedas (1999) Differents. Uravn. 35 IssueID9 1253–1261

    Google Scholar 

  2. A.A. Pedas E. Timak (2001) Differents. Uravn. 37 IssueID10 1415–1424

    Google Scholar 

  3. R.R. Pallav A.A. Pedas (2003) Differents. Uravn. 39 IssueID9 1272–1281

    Google Scholar 

  4. H. Brunner A. Pedas G. Vainikko (1999) Math. Comp. 68 IssueID227 1079–1095

    Google Scholar 

  5. H. Brunner A. Pedas G. Vainikko (2001) SIAM J. Numer. Anal. 39 IssueID3 957–982

    Google Scholar 

  6. H. Brunner A. Pedas G. Vainikko (2001) BIT 41 IssueID5 891–900

    Google Scholar 

  7. Parts, I. and Pedas, A., in Numerical Mathematics and Advanced Applications, Enumath 2001, Brezzi, F., Buffa, A., Corsaro, S., and Murli, A., Eds., Milano, 2003, pp. 919–928.

  8. Brunner, H. and van der Houwen, P.J., The Numerical Solution of Volterra Equations, Amsterdam, 1986.

  9. H. Brunner (1986) IMA J. Numer. Anal. 6 221–239

    Google Scholar 

  10. T. Tang (1992) Numer. Math. 61 373–382

    Google Scholar 

  11. T. Tang (1993) IMA J. Numer. Anal. 13 93–99

    Google Scholar 

  12. J. Norbury A.M. Stuart (1987) Proc. Roy. Soc. Edinburgh 106 A 361–373

    Google Scholar 

  13. J. Abdalkhani (1993) J. Integral Equations Appl. 5 IssueID2 149–166

    Google Scholar 

  14. T. Diogo S. McKee T. Tang (1994) Proc. Roy. Soc. Edinburgh 124 A 199–210

    Google Scholar 

  15. G. Monegato L. Scuderi (1998) Math. Comput. 67 IssueID224 1493–1515

    Google Scholar 

  16. E.A. Galperin E.J. Kansa A. Makroglou S.A. Nelson (2000) J. Comput. Appl. Math. 115 93–211

    Google Scholar 

  17. A. Pedas G. Vainikko (2004) Proc. Estonian Acad. Sci. Phys. Math. 53 IssueID2 99–106

    Google Scholar 

  18. Q. Hu (1998) IMA J. Numer. Anal. 18 151–164

    Google Scholar 

  19. S.G. Krantz (1992) Theory of Several Complex Variables Pacific Grove California

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Applied Mathematics, Tartu State University, Tartu, Estonia

    A. A. Pedas

Authors
  1. A. A. Pedas
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Translated from Differentsial’nye Uravneniya, Vol. 40, No. 9, 2004, pp. 1271–1279.

Original Russian Text Copyright © 2004 by Pedas.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pedas, A.A. On the approximate solution of weakly singular integro-differential equations of Volterra type. Diff Equat 40, 1345–1353 (2004). https://doi.org/10.1007/s10625-005-0013-9

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10625-005-0013-9

Keywords

Search

Navigation