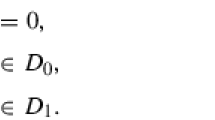Skip to main content
SpringerLink
Log in

Large classes of permutation polynomials over \(\mathbb {F}_{q^2}\)

  • Published:
Designs, Codes and Cryptography Aims and scope Submit manuscript

Abstract

Permutation polynomials (PPs) of the form \((x^{q} -x + c)^{\frac{q^2 -1}{3}+1} +x\) over \(\mathbb {F}_{q^2}\) were presented by Li et al. (Finite Fields Appl 22:16–23, 2013). More recently, we have constructed PPs of the form \((x^{q} + bx + c)^{\frac{q^2 -1}{d}+1} -bx\) over \(\mathbb {F}_{q^2}\), where \(d=2, 3, 4, 6\) (Yuan and Zheng in Finite Fields Appl 35:215–230, 2015). In this paper we concentrate our efforts on the PPs of more general form

$$\begin{aligned} f(x)=(ax^{q} +bx +c)^r \phi \big ((ax^{q} +bx +c)^{(q^2 -1)/d}\big ) +ux^{q} +vx ~{\text {over}}\; \mathbb {F}_{q^2}, \end{aligned}$$

where \(a,b,c,u,v \in \mathbb {F}_{q^2}\), \(r \in \mathbb {Z}^{+}\), \(\phi (x)\in \mathbb {F}_{q^2}[x]\) and d is an arbitrary positive divisor of \(q^2-1\). The key step is the construction of a commutative diagram with specific properties, which is the basis of the Akbary–Ghioca–Wang (AGW) criterion. By employing the AGW criterion two times, we reduce the problem of determining whether f(x) permutes \(\mathbb {F}_{q^2}\) to that of verifying whether two more polynomials permute two subsets of \(\mathbb {F}_{q^2}\). As a consequence, we find a series of simple conditions for f(x) to be a PP of \(\mathbb {F}_{q^2}\). These results unify and generalize some known classes of PPs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Akbary A., Ghioca D., Wang Q.: On constructing permutations of finite fields. Finite Fields Appl. 17, 51–67 (2011).

  2. Cao X., Hu L., Zha Z.: Constructing permutation polynomials from piecewise permutations. Finite Fields Appl. 26, 162–174 (2014).

  3. Charpin P., Kyureghyan G.: When does \(G(x) +\gamma Tr(H(x))\) permute \({\mathbb{F}}_{p^n}\)? Finite Fields Appl. 15(5), 615–632 (2009).

  4. Ding C., Xiang Q., Yuan J., Yuan P.: Explicit classes of permutation polynomials of \({\mathbb{F}}_{3^{3m}}\). Sci. China Ser. A 53(4), 639–647 (2009).

  5. Ding C., Zhou Z.: Binary cyclic codes from explicit polynomials over GF\((2^m)\). Discret. Math. 321, 76–89 (2014).

  6. Fernando N., Hou X.: A piecewise construction of permutation polynomial over finite fields. Finite Fields Appl. 18, 1184–1194 (2012).

  7. Hou X.: A new approach to permutation polynomials over finite fields. Finite Fields Appl. 18(3), 492–521 (2012).

  8. Hou X.: Permutation polynomials over finite fields—a survey of recent advances. Finite Fields Appl. 32, 82–119 (2015).

  9. Laigle-Chapuy Y.: Permutation polynomials and applications to coding theory. Finite Fields Appl. 13(1), 58–70 (2007).

  10. Li N., Helleseth T., Tang X.: Further results on a class of permutation polynomials over finite fields. Finite Fields Appl. 22, 16–23 (2013).

  11. Lidl R., Müller W.B.: Permutation polynomials in RSA-cryptosystems. In: Advances in Cryptology, pp. 293–301. Plenum Press, New York (1984).

  12. Lidl R., Mullen G.L.: When does a polynomial over a finite field permute the elements of the field? Am. Math. Mon. 95(3), 243–246 (1988).

  13. Lidl R., Mullen G.L.: When does a polynomial over a finite field permute the elements of the field? II. Am. Math. Mon. 100(1), 71–74 (1993).

  14. Lidl R., Niederreiter H.: Finite Fields. Cambridge University Press, Cambridge (1997).

  15. Mullen G.L.: Permutation polynomials over finite fields. In: Finite Fields, Coding Theory, and Advances in Communications and Computing, pp. 131–151. Dekker, New York (1993).

  16. Mullen G.L., Panario D.: Handbook of Finite Fields. CRC Press, Boca Raton (2013).

  17. Niederreiter H., Robinson K.H.: Complete mappings of finite fields. J. Aust. Math. Soc. Ser. A 33, 197–212 (1982).

  18. Rivest R.L., Shamir A., Adelman L.M.: A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21, 120–126 (1978).

  19. Shaheen R., Winterhof A.: Permutations of finite fields for check digit systems. Des. Codes Cryptogr. 57, 361–371 (2010).

  20. Singh R.P., Saikia A., Sarma B.K.: Poly-dragon: an efficient multivariate public key cryptosystem. J. Math. Cryptol. 4, 349–364 (2011).

  21. Stǎnicǎ P., Gangopadhyay S., Chaturvedi A., Gangopadhyay A.K., Maitra S.: Investigations on Bent and Negabent Functions via the Nega–Hadamard Transform. IEEE Trans. Inf. Theory 58(6), 4064–4072 (2012).

  22. Tu Z., Zeng X., Hu L.: Several classes of complete permutation polynomials. Finite Fields Appl. 25, 182–193 (2014).

  23. Wang Q.: Cyclotomy and permutation polynomials of large indices. Finite Fields Appl. 22, 57–69 (2013).

  24. Wu B.: The compositional inverse of a class of linearized permutation polynomials over \({\mathbb{F}}_{2n}\), n odd. Finite Fields Appl. 29, 34–48 (2014).

  25. Yuan J., Ding C., Wang H., Pieprzyk J.: Permutation polynomials of the form \((x^p - x + \delta )^s + L(x)\). Finite Fields Appl. 14, 482–493 (2008).

  26. Yuan P., Ding C.: Permutation polynomials over finite fields from a powerful lemma. Finite Fields Appl. 17, 560–574 (2011).

  27. Yuan P., Ding C.: Further results on permutation polynomials over finite fields. Finite Fields Appl. 27, 88–103 (2014).

  28. Yuan P., Zheng Y.: Permutation polynomials from piecewise functions. Finite Fields Appl. 35, 215–230 (2015).

  29. Zeng X., Zhu X., Hu L.: Two new permutation polynomials with the form \((x^{2^k}+x+\delta )^s+x\) over \({\mathbb{F}}_{2^n}\). Appl. Algebra Eng. Commun. Comput. 21, 145–150 (2010).

  30. Zha Z., Hu L.: Two classes of permutation polynomials over finite fields. Finite Fields Appl. 18, 781–790 (2012).

  31. Zha Z., Hu L., Cao X.: Constructing permutations and complete permutations over finite fields via subfield-valued polynomials. Finite Fields Appl. 31, 162–177 (2015).

  32. Zheng Y., Yuan P., Pei D.: Piecewise constructions of inverses of some permutation polynomials. Finite Fields Appl. 36, 151–169 (2015).

  33. Zieve M.E.: On some permutation polynomials over \({\mathbb{F}}_q\) of the form \(x^rh(x^{(q-1)/d})\). Proc. Am. Math. Soc. 137, 209–216 (2009).

Download references

Acknowledgments

We are grateful to the two anonymous referees for useful comments and suggestions. This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 11371106, 11271142, 61363069) and the Guangdong Provincial Natural Science Foundation (Grant No. S2012010009942).

Author information

Authors and Affiliations

  1. Guangxi Key Laboratory of Trusted Software, Guilin University of Electronic Technology, Guilin, China

    Yanbin Zheng

  2. School of Computer Science and Engineering, Guilin University of Electronic Technology, Guilin, China

    Yanbin Zheng

  3. School of Mathematics, South China Normal University, Guangzhou, China

    Pingzhi Yuan

  4. School of Mathematics and Information Science, Guangzhou University, Guangzhou, China

    Yanbin Zheng & Dingyi Pei

  5. Key Laboratory of Mathematics and Interdisciplinary Sciences of Guangdong Higher Education Institutes, Guangzhou University, Guangzhou, China

    Yanbin Zheng & Dingyi Pei

Authors
  1. Yanbin Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pingzhi Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dingyi Pei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yanbin Zheng.

Additional information

Communicated by T. Helleseth.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zheng, Y., Yuan, P. & Pei, D. Large classes of permutation polynomials over \(\mathbb {F}_{q^2}\) . Des. Codes Cryptogr. 81, 505–521 (2016). https://doi.org/10.1007/s10623-015-0172-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10623-015-0172-5

Keywords

Mathematics Subject Classification

Search

Navigation