TenGAN: adversarially generating multiplex tensor graphs

Abstract

In this work, we explore multiplex graph (networks with different types of edges) generation with deep generative models. We discuss some of the challenges associated with multiplex graph generation that make it a more difficult problem than traditional graph generation. We propose TenGAN, the first neural network for multiplex graph generation, which greatly reduces the number of parameters required for multiplex graph generation. We also propose 3 different criteria for evaluating the quality of generated graphs: a graph-attribute-based, a classifier-based, and a tensor-based method. We evaluate its performance on 4 datasets and show that it generally performs better than other existing statistical multiplex graph generative models. We also adapt HGEN, an existing deep generative model for heterogeneous information networks, to work for multiplex graphs and show that our method generally performs better.

1 Introduction

Graphs are used to represent many different types of data—from protein interactions (Pavlopoulos et al. 2011) to social networks (Newman et al. 2002). There are a similarly large number of useful graph-related tasks, like link prediction and node classification. One of these tasks is graph generation, which is the focus of this work. Graph generation models can generally be split into two types: statistical attribute-based generative models and deep generative models. Statistical generative models like the Erdös and Rényi (1959), Barabási and Albert (1999), and stochastic block models (Holland et al. 1983) have explicitly defined parameters like the attachment rate or the number of communities.

In contrast, many deep generative models can learn directly from one or more input graphs. This ability allows them to mimic attributes of the input dataset without defining them explicitly. The majority of these models are based on either RNNs (Recurrent Neural Networks), GANs (Generative Adversarial Networks) (Goodfellow et al. 2020), or VAEs (Variational Autoencoders) (Kingma and Welling 2013). Examples of these include GraphRNN (You et al. 2018), NetGAN (Bojchevski et al. 2018), GraphVAE (Kipf and Welling 2016), and LGGAN (Fan and Huang 2019).

However, sometimes a simple graph structure may not be sufficient to represent a dataset accurately. One example of this is the Enron dataset (Klimt and Yang 2004), where each node is a person and each edge is an email between them. Representing this as a standard graph would only show that two people communicated with each other, without any information on when they communicated. For example, the two people may have exchanged an email once, daily, or once a month–each of which would indicate a very different relationship. Representing this data as a multiplex graph allows us to fully represent this information.

Another use-case for a multiplex graph is to capture different types of social media interactions across the same users. Each node would represent a person and each edge type could represent a different form of interaction. An example of this could be a graph representing Twitter interactions, where each edge could either represent a retweet, mention, or following. Using only one of these would unecessarily limit the information captured in the graph.

Traditional graph generation models and multiplex graph generation models are useful in many of the same ways. For example, they can be used to anonymize private data (Wang and Wu 2013) in order to enhance the reproducibility of models trained on private datasets. This would allow the user to preserve interesting structures in the graph without leaking private user information.

However, all of the current multiplex network generation models are statistical generative models. BINBALL (Basu et al. 2015) adapts ideas from BA and ER models and proposes new multiplex preferential attachment rules. StarGen (Fügenschuh et al. 2018) further builds upon BINBALL by separating the parameters controlling the global and local degree of nodes, increasing the diversity of individual layers. ANGEL (Fügenschuh et al. 2020) uses a hub-and-spoke-based model to generate multiplex graphs, allowing it to better mimic certain structures. These existing works pose some major limitations, namely:

• 1. Explicit parameterization. The existing models declare a set of parameters that affect the output of the graph. These parameters are inflexible and may lead to overfitting to a particular graph attribute while neglecting another.

• 2. Limited datasets. All three of the methods focus on Airline Transportation Networks (ATNs), specifically on the EU airline dataset (Cardillo et al. 2013). It is difficult to determine if the methods will work for different datasets. In this work, we explore the task of multiplex graph generation on datasets from wildly varying domains.

• 3. Limited evaluation criteria. It is difficult to quickly compare the performance of the models on different datasets. The performance evaluation of the models is primarily done visually by comparing the distributions of various topological properties. This also ignores some other potentially interesting characteristics of the generated graphs like whether or not a classifier can distinguish between real and generated samples, especially useful for tasks like graph anonymization.

The first problems can be resolved by using a neural network to learn directly from a set of input graphs. However, extending a traditional graph generation network is not straightforward since the layers are often correlated. There are also many more parameters required. Furthermore, it is difficult to evaluate the quality of the generated graphs. We further investigate these issues in Sect. 3 below.

In this work, we tackle these issues and propose TenGAN, a tensor-based GAN, to generate multi-view graphs. With minor modifications, our approach readily generalizes to other data sources that can be modelled well with tensor decompositions. For example, tensor decompositions have been shown to work well on a variety of data, including fMRI (Noroozi and Rezghi 2020) and EEG data (Cong et al. 2015), NBA game data (Papalexakis and Pelechrinis 2018), network traffic data (Baskaran et al. 2019), and spatio-temporal urban computing data (Wang et al. 2014). However, in this work, we focus on the domain of multiplex graphs and reserve exploring other domains for future work.

Our contributions include:

• Novel method: We propose a novel GAN-based method to generate multiplex graphs that uses tensor decomposition to reduce the number of parameters required.

• Evaluation criteria: We propose 3 different evaluation metrics for multiplex graph generation and evaluate their effectiveness.

• Thorough experimentation: We conduct thorough experiments on 4 different datasets across 2 different models to evaluate the performance of our method. We also modify an existing method for heterogeneous graphs to work with multiplex graphs and compare our method against it.

2 Background

We first enumerate important background information and notation for this work. We briefly define and describe multiplex graphs, tensors, tensor decompositions, and generative adversarial networks. A table of symbols can be found in Table 1.

Table 1 Table of symbols and their description

2.1 Multiplex graphs

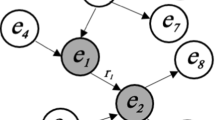
In this work, we focus on the generation of multiplex graphs. A multiplex graph consists of several views, where each view is a graph. Each of the views contains the same nodes, but with different edges. Formally, a multiplex graph G with k views can be written as $G = (V, (E_1, E_2, \ldots E_k))$, where V is the shared vertex set and $E_i$ are the edges at the i-th layer. It is worth noting that not all of the nodes need to be connected within each view.

One example of a multiplex graph is a social network, where each edge in a given view represents a different mode of communication. A time-evolving graph with a constant number of nodes could also be represented as a multiplex graph, with each view representing a different timestamp. Finally, a knowledge base could be seen as a multiplex graph, where each node represents an entity and each view represents a different relation. It is worth noting that this differs from the traditional notion of a multigraph, where nodes can have multiple edges between them but each edge is of the same type. Edges in a multiplex graph can have multiple types.

2.2 Tensors & decompositions

Networked data (e.g., a social network) can be represented in many different formats. One of the most common formats is to use an adjacency matrix. In a similar manner, a multiplex graph can be viewed as a third-order tensor where $\varvec{\mathcal {T}}_{i,j,k} = w$ if there is an edge of weight w (or 1 in the case of an unweighted graph) between node i and node j in view k. A visual example of this is shown below in Fig. 1.

Fig. 1

Example of a multiplex graph being represented as a tensor. Left: each view of the multiplex graph (can be seen as a graph). Middle: each view shown as an adjacency matrix. Right: the adjacency tensor consisting of the stacked slices

One advantage of storing multiplex graphs in this tensor format is that it allows us to easily apply tensor decomposition methods. One of the most common tensor decomposition methods is the CANDECOMP/PARAFAC or Canonical Polyadic Decomposition (CPD) (Hitchcock 1927; Kolda and Bader 2009). Given an integer r, the CPD decomposes a tensor $\varvec{\mathcal {T}}$ into the sum of r outer products of vectors. While the CPD can be applied to a tensor of any order, we focus on the third-order case in this work. Thus, the CPD can be written as:

$${\mathcal{T}} \approx {\text{ }}{\mathbf{A}},{\mathbf{B}},{\mathbf{C}} = \sum\limits_{{i = 1}}^{r} {a_{i} ^\circ \;b_{i} ^\circ \;{\text{ }}c_{i} }$$

where $\varvec{a}_i, \varvec{b}_i, \varvec{c}_i$ are the factor vectors. It is convention to write the factors as matrices $\textbf{A}, \textbf{B}, \textbf{C}$, which consist of the corresponding vectors horizontally stacked. For example, the i-th column of $\textbf{A}$ would be $\varvec{a}_i$.

Another tensor decomposition method that has been shown to work well in the domain of knowledge bases and other multiplex graphs is RESCAL (Nickel et al. 2011). Given a $I \times J \times K$ tensor $\varvec{\mathcal {T}}$, RESCAL factors each slice as $\varvec{\mathcal {T}}^{(i)} \approx \textbf{A} \varvec{\mathcal {R}}^{(i)} \textbf{A}^{T}$, where $\textbf{A}$ is $n \times r$ and $\varvec{\mathcal {R}}$ is $r \times r \times K$.

2.3 Graph convolutional networks (GCNs)

Kipf and Welling (2017) propose graph convolutional networks (GCNs), which convolves the features of a given node with the features of its neighbors. Each additional GCN layer incorporates information from another hop in the graph. Formally, each layer of the GCN can be written as:

$$\begin{aligned} \varvec{h}_u^{(k+1)} = \sigma \left( \textbf{W}^{(k+1)} \sum _{v\in \textsc {Neigh}(u) \cup \{ u \}} \frac{\varvec{h}_v}{\sqrt{| \textsc {Neigh}(u) | \cdot | \textsc {Neigh}(v) |}} \right) \end{aligned}$$

(1)

where $\varvec{h}_u^{(k)}$ is the representation of u at the k-th layer, $\textbf{W}^{(k)}$ are the weights of k-th layer, and $\varvec{h}_u^{(0)}$ are the node features of u. Note that we focus on featureless multiplex graphs in this work. As such, we set $\varvec{h}_u^{(0)} = I$; essentially setting the node features of each node equal to its one-hot encoding.

2.4 Generative adversarial networks (GANs)

In this work we use a GAN (Goodfellow et al. 2020) architecture which, in its general form includes a generator network that generates “fake” data and a discriminator network that distinguishes fake from real. Both networks trained in unison and are engaged in a game of outperforming each other, with the end goal being that the generator can essentially learn the distribution of real data. One challenge of this approach is that we need a distribution of inputs to model over, rather than just a single sample. We discuss how we address this in Sect. 4.1.

3 Problem formulation

We consider the following problem:

Some examples of criteria in $\mathcal {C}$ may include graph attributes (like clustering coefficient and degree distribution) or the correlation between different slices. However, it is not fully clear what these criteria should be and is one of several challenges in multiplex graph generation, some of which are listed below:

• Challenge 1: Inadequate Evaluation Criteria Before we can decide on an appropriate model, we must determine our evaluation criteria. This is challenging because we need to consider not only the graph attributes of each view but also the relationships between each view. This means that many of the graph evaluation metrics commonly used in graph generation are insufficient for multiplex graph generation. In this work, we propose 3 methods of evaluation for multiplex graph generation models, described in Sect. 4.4 below.

• Challenge 2: Sampling from Multiplex Graphs Many existing multiplex datasets consist of a single graph with multiple views. However, since we are emulating a set of multiplex graphs, we need many smaller multiplex graphs to form a distribution. In the traditional graph setting, there are existing datasets that consist of multiple graphs (e.g., the PPA dataset (Hu et al. 2020)). However, to the best of our knowledge, there are no such existing datasets for multiplex graphs. Therefore, we need a sampling method that samples smaller multiplex sub-graphs from a larger multiplex graph. We describe our method in Sect. 4.1 below.

• Challenge 3: Large Number of Parameters If we naively attempt to generate a multiplex graph, the number of parameters required will explode. This is because we need parameters to generate an adjacency tensor for a multiplex graph with k views and n nodes. We propose TenGAN (described in Sect. 4.2) that generates a compressed tensor-decomposition-based representation to solve this problem.

4 Proposed method

We propose TenGAN, a GAN-based model that first generates factors of a tensor decomposition model, then uses those to generate the adjacency tensor. We propose two variants: TenGAN-CP, which uses the CPD and TenGAN-R, which uses the RESCAL decomposition. We first sample sub-multiplex graphs from the dataset, as described in Sect. 4.1. Then, we train our GAN on the sampled multiplex graphs. Finally, we sample random graphs from the generator (by passing in different random noise vectors) and evaluate them with the metrics described in Sect. 4.4.

4.1 Sampling

Many generative models require multiple input samples, rather than a single example. For example, LGGAN (Fan and Huang 2019) is trained on 2-hop and 3-hop egonets extracted from the original source graph. However, it has been shown that this can lead to biased samples that may not necessarily be representative of the original graph, especially in terms of in-degree and community structure (Leskovec and Faloutsos 2006). To help avoid this, we perform random-walk sampling across each view. We then use the induced subgraph on the remainder of the views.

However, one issue with many large multiplex datasets is that most of the nodes may be disconnected in any given view. In extreme examples, like in some knowledge graphs, almost all nodes will be disconnected in each view. Oftentimes, even the union of all edges across all views will still result in a disconnected graph.

Another issue is that these datasets are often too large or have too many views. For example, the NELL dataset (Carlson et al. 2010; Smith et al. 2017) has over 2 million views. Random sampling of the dataset would produce extremely or completely sparse entries. In order to produce better quality samples, we use the sampling method of ParCube (Papalexakis et al. 2012).

This computes the following importance score for each slice along each mode. For example, the importance scores for each slice along the three modes for a tensor $\varvec{\mathcal {T}}$ would, respectively, be:

$$\begin{aligned} \varvec{a}_i = \sum ^J_{j=1} \sum ^K_{k=1} \varvec{\mathcal {T}}_{i,j,k}; \ \ \varvec{b}_j = \sum ^I_{i=1} \sum ^K_{k=1} \varvec{\mathcal {T}}_{i,j,k}; \ \ \varvec{c}_k = \sum ^I_{i=1} \sum ^J_{j=1} \varvec{\mathcal {T}}_{i,j,k} \end{aligned}$$

We then randomly sample indices for each mode, with the probability of a given index being selected proportional to its score. For example, a given index i is selected with probability $\varvec{a}_i / \sum ^{I}_{x=1} \varvec{a}_x$. This results in a more dense tensor and therefore a multiplex graph with more connected nodes, reducing the chance of getting empty (or near-empty) tensors as inputs to our model.

4.2 Architecture

Our model is a GAN and consists of a generator network and a discriminator network. The generator consists of a MLP, followed by two or three smaller MLPs to generate the factor matrices/tensors (depending on the factorization method). We further describe the two generator architectures below in Sects. 4.2.1, and 4.2.2. The discriminator uses the max pool of several Graph Convolutional Networks (GCNs) (Kipf and Welling 2017) (one per view) followed by a fully-connected layer to predict if a sample is generated or drawn from the original real dataset. A diagram of our architecture is shown in Fig. 2.

4.2.1 TenGAN-CP architecture

TenGAN-CP uses a shared feature extractor layer and splits into separate networks, each of which generates a different factor in the CPD. This can be considered a higher-order extension of the BRGAN-B (Shiao and Papalexakis 2021) architecture and uses the tensor CPD instead of the matrix SVD.

After generating the factors, we calculate the sum of the outer products of vectors from our factor matrices $\textbf{A}, \textbf{B}$, and $\textbf{C}$: $\sum ^r_{i=1} \varvec{a}_i \circ \varvec{b}_i \circ \varvec{c}_i$. As shown in Sect. 4.3, this reduces the number of parameters needed to generate a given multiplex graph. We use the loss function from Wei et al. (2018) (which is based on Arjovsky et al. (2017)):

$$\begin{aligned} L = \underset{{\llbracket \textbf{A}, \textbf{B}, \textbf{C} \rrbracket }\sim \mathbb {P}_g}{\mathbb {E}} \left[ D( {\llbracket \textbf{A}, \textbf{B}, \textbf{C} \rrbracket }) \right] - \underset{\textbf{x} \sim \mathbb {P}_r }{\mathbb {E}} \left[ D(\varvec{x}) \right] + \lambda _1 \textsc {GP} + \lambda _2 \textsc {CT} \end{aligned}$$

where GP is the gradient penalty term from Gulrajani et al. (2017), CT is the consistency term from Wei et al. (2018), and ${\textbf{A}},{\textbf{B}},{\textbf{C}}$ is the output from the generator. $\mathbb {P}_g$ denotes the distribution of graphs generated by the generator, and $\mathbb {P}_r$ denotes the real distribution of graphs. $D(\cdot )$ denotes the output of the discriminator on a given tensor. The goal of this loss function is to minimize the difference between the expected values of the discriminator’s output on the generated data and the input (real) data.

4.2.2 TenGAN-R architecture

We also propose the TenGAN-R architecture, which is initially similar to the TenGAN-CP architecture, with the distinction that we use the RESCAL decomposition instead of the CPD. This results in more parameters for the same value of r, but performs better on certain datasets (Table 3).

Fig. 2

Diagram of the TenGAN discriminator (top) and two different generator architectures (bottom). TenGAN-CP is based on the CP decomposition, and generates the factor matrices $\textbf{A}, \textbf{B}, \textbf{C}$ before combining them into the output adjacency tensor. TenGAN-R is based on the RESCAL decomposition, and first generates the factor matrix $\textbf{A}$ and factor tensor $\varvec{\mathcal {R}}$ before combining them into the adjacency tensor

4.3 Parameter complexity

If we attempted to generate an adjacency tensor for a multiplex graph with n nodes and k views directly, we would have to use parameters in the final layer. However, if we generate the CPD factors first, we only need parameters in the final layer, where r is a hyperparameter that increases the quality of the fit at the cost of more parameters. This offers savings for $r < n^2$, and we show that our models work well for this case in Table 3. For the RESCAL-based formulation, we need parameters in the final layer. In this case, we only reduce the number of parameters in the case where $r < n$.

4.4 Evaluation metrics

Another difficult task in multiplex graph generation is evaluating the quality of the generated graphs. Gretton et al. (2012) found that measuring the Maximum Mean Discrepancy (MMD) between distributions of different graph statistics works well for simple graphs. We propose 3 methods for evaluating the structural similarity between generated and input graphs:

4.4.1 MMD-based evaluation

One method to evaluate the quality of generated multiplex graphs would be to apply the evaluation criteria used for simple graphs to each view. We measure the Mean MMD (M-MMD) score between the distributions of different graph attributes. More concretely, for each graph attribute, we take the mean of the MMD between the i-th view of a generated graph $G'$ and a graph G. We can use the clustering coefficient, degree distribution, and the orbit of the graphs similar to You et al. (2018).

The main downside of this approach is that it does not take the relationship between the views into account. For example, consider the case where we generate multiplex graphs with two views. Let the list of the generated first and second views be $V'_1 = g'^{(1)}\forall g' \in G'$ and $V'_2 = g'^{(2)}\forall g' \in G'$. Then, suppose the MMD scores of $V'_1$ and $V'_2$ across all the graph attributes are 0. Then, the overall Mean MMD (M-MMD) would be 0. However, swapping $V'_1$ and $V'_2$, yields same M-MMD.

This is clearly an undesirable behavior in any case where each of the views are correlated with each other. An extreme example of this would be a multiplex graph g where $g^{(1)}$ has an edge iff $g^{(2)}$ does not have an edge. Then, it is possible for a generated graph $g'$ to have $g'^{(1)} = g'^{(2)}$, but still have a perfect M-MMD of 0 in all the graph attributes. To address this issue, we propose the tensor-based evaluation method below.

Fig. 3

Three plots of pairs of CPD error values that have low, medium, and high EMD scores. CPD error vs. rank plot on three pairs of tensors. The dashed green lines are the generated results, and the solid blue lines are the original results. We can see that the EMD scores are lower when the lines are more similar and that the scores are higher when the lines are further apart. This is the intuition behind our tensor-based evaluation method

4.4.2 Tensor-based evaluation

Multiplex graphs can be viewed as third-order tensors, where each slice is a graph across the same nodes, and tensor decompositions have been shown to be able to extract structure (like communities) from multiplex graphs (Gujral and Papalexakis 2018; Gauvin et al. 2014; Al-Sharoa et al. 2017; Sheikholeslami and Giannakis 2018). We take advantage of this fact by applying the CPD to each multiplex graph or tensor. The normalized reconstruction error of the decomposition for various values of r provides a heuristic for how much structure there is along the three modes of the tensor. We then compare the errors of the generated and original tensors across different ranks to see if they are similar in terms of trilinear structure. It may be possible to produce a similar reconstruction error for a given rank without matching the structure of the real graph, but we argue that it is highly unlikely for this to occur across many different values of r.

We randomly sample n tensors from the generated and real tensors and compute an error vector $\textbf{e}$ of the errors across different ranks. We then calculate the sum of the Wasserstein metric (a.k.a. the earth mover’s distance: EMD) between all $n^2$ pairs of error vectors. The lower this score, the more similar pairs are (on average). While this score works well across a fixed dataset, it is difficult to compare this score across datasets of different sizes. This is because the number of feasible r values changes with the size of the tensor; and a given dataset may naturally have a wider range of pairwise distances (Fig. 3).

To solve this issue, we normalize the sum of generated-real distances by the sum of pairwise real-real distances. More formally, given real error matrix $\textbf{E}$ and generated error matrix $\mathbf {E'}$ (where every row $\textbf{E}_i$ is a vector of the i-th sample’s CPD errors):

$$\begin{aligned} \textsc {TenScore} = \frac{\sum ^n_{i=1} \sum ^n_{j=1} \textsf {EMD}(\textbf{E}_i, \mathbf {E'}_j)}{\sum ^n_{i=1} \sum ^n_{j=1} \textsf {EMD}(\textbf{E}_i, \textbf{E}_j)} \end{aligned}$$

(2)

The lower the TenScore, the more realistic the generated samples are. TenScore also serves as an indicator for graph diversity. If it near 0, it likely means that the model is suffering from mode collapse—a common problem among GANs. We also propose a modified version of TenScore for knowledge base graphs: TenScore-R, which uses RESCAL’s error.

Fig. 4

Diagram of the classifier-based evaluation model. We first calculate an embedding and train a classifier on each view before using the majority vote to guess if the result is a real or generated multiplex graph. Note that this is similar to, but different from the discriminator. This is because we use an established embedding model and a non-neural-network classifier

4.4.3 Classifier-based evaluation

We train a classifier on generated and original data; then check to see if it correctly predicts the origin of an example. We calculate the accuracy and F1 score of the resulting model (the closer to 0.5 or 50%, the better). In the model, we calculate a graph2vec (Narayanan et al. 2017) embedding for each view of the multiplex graph. Then, we split the embeddings into training/test data and train a SVM classifier for each view. Finally, we take the majority vote of the ensemble. These steps are shown in a diagram in Fig. 4.

4.5 Implementation details

We implemented this model in PyTorch (Paszke et al. 2019) on Python 3.9. We used NetworKit (Staudt et al. 2016) and NetworkX (Hagberg et al. 2008) for graph data, and Tensorly (Kossaifi et al. 2016) for tensor decompositions. We extended portions of the GraphRNN (You et al. 2018) evaluation code and heavily modified HGEN (Ling et al. 2021) to work for multiplex graphs (see details in Sect. 5.2). We use the code from Rossetti (2020) for the BINBALL, StarGen, and ANGEL baselines. It was originally written for undirected networks, so we extend it to work for directed multiplex graphs. The code for our experiments is available here.¹

5 Experimental evaluation

5.1 Datasets

We used 4 multiplex graph datasets selected to represent a wide variety of data types, including a social media network, a knowledge graph, a computer network communication graph, and a time-evolving network.

• 1. Football (Greene and Cunningham 2013): 248 English Premier League football players and clubs on Twitter, where each of the 6 views corresponds to a different interaction between the accounts (follows, followed-by, mentions, mentioned-by, retweets, retweeted-by). Note that 3 of the views are essentially transposes of the other 3.

• 2. NELL-2 (Carlson et al. 2010): A sampled version of the NELL-2 dataset (from Smith et al. (2017)) that consists of (entity, relation, entity) tuples. The original size is $12,092 \times 9,184 \times 28,818$, but we resample it to a $1,000 \times 4 \times 1,000$ tensor (where 4 is the number of views) for the purpose of evaluation. The sampling method is described in Sect. 4.1.

• 3. Comm: An enterprise communication network dataset of 1,558,594 computers. Each view corresponds to communications between nodes on one of five ports (22, 23, 80, 443, and 445), with one view for each port. In the view associated with port p, a directed edge from u to v exists if u initiates a connection to v over port p. Since we are unable to provide a copy of this network, descriptive statistics of each view in this network are shown below in Table 2.

• 4. Enron (Klimt and Yang 2004): A multiplex graph of emails sent between Enron employees, where each view represents a two-month (60-day) time interval and edges represent emails. The original tensor (available at Smith et al. (2017)) is 6,066 senders $\times$ 5,699 recipients $\times$ 244,268 words $\times$ 1,176 days. We collapse the words dimension and simply add an unweighted edge for each email sent in a given time interval. We also aggregate the slices so that each view represents a 60-day period to reduce the number of views. Finally, we sample 1,000 senders and 1,000 recipients using the methodology described in the supplementary material. Finally, we sample 1,000 senders and 1,000 recipients using the methodology described in Sect. 4.1.

We perform random walk sampling to extract a set of sub-multiplex-graphs from each dataset. We describe this process with more detail in Sect. 4.1.

Table 2 Since we are unable to share the data for the comm dataset, we instead provide network statistics of the computer infrastructure graph

5.2 Comparison with existing methods

To the best of our knowledge, no other deep learning models for multiplex graph generation exist. The existing models are statistical and are built to match specific attributes of the underlying graph. We compare our method against BINBALL (Basu et al. 2015), StarGen (Fügenschuh et al. 2018), and ANGEL (Fügenschuh et al. 2020). We also adapt HGEN (Ling et al. 2021)—a generative model for heterogeneous graphs—to work for multiplex graphs. A heterogeneous graph consists of nodes of different types and, therefore, edges of different types. An common example of this is a citation graph, where we might have nodes for authors, papers, and conferences. This is in contrast to multiplex graphs, where we have different views of the same nodes. As such, it is difficult to directly compare the two methods—however, we attempt to convert multiplex graphs to heterogeneous graphs and evaluate its performance. The HGEN code² (as provided in the paper) does not support different edge types or a single node belonging to multiple classes, so we encountered the following issues (some of which may affect its performance).

Lack of multiplex graph support. Let n be the number of nodes and k be the number of views in our original multiplex graph. To work around the lack of support for different edge types, we create k nodes for each of the n nodes in the original graph, each with a different class in the range [1, k]. Then, we link together each of these k nodes in the heterogeneous network. This results in a total of nk nodes across k classes in the resulting heterogeneous network.

Graph size issues. While the actual HGEN model is efficient for generation, it requires HIN node embeddings for each node in the input graph. We chose to use hin2vec (Fu et al. 2017)— same as in the original HGEN code. However, we have nk nodes after the conversion to a HIN, causing the embeddings to take too long to calculate on some datasets (like the Comm dataset).

Table 3 Results of TenGAN on the football, NELL-2, enron, and comm datasets. Lower is better for all of these metrics, including F1/Acc. deg, clust, and orbit are the mean MMD scores of our MMD-based evaluation method (see Sect. 5.3)

5.3 MMD-based evaluation

The MMD-based evaluations compares the similarity of different graph attributes for each slice between the real and generated graphs. From Table 3, we can see that TenGAN-CP and TenGAN-R generally perform fairly well on the Football, NELL-2 and Comm datasets. However, this is a layer-level comparison, and even BA (which treats each layer separately) performs decently well in this comparison. This is why the other evaluation methods are important, especially the tensor-based evaluation, which provides a holistic look at the generated tensors.

5.4 TenScore evaluation

TenGAN-CP tends to perform best in terms of TenScore across all the datasets, with the exception of the Comm dataset (where BINBALL performs slightly better). TenGAN-CP has a TenScore of below 1 on the Football, NELL-2, and Enron datasets. This indicates that the mean EMD for all real-generated pairs is lower than the mean EMD for all real-real pairs in the dataset. None of the methods have a very low TenScore, which means that all of the methods exhibit a good amount of diversity comparable to that of the original data. However, some of the baseline methods have a very high TenScore, indicating that the generated graphs have a very different amount of trilinear structure from that of the input graphs.

Suprisingly, Barabási-Albert outperforms some of the other statistical methods on the Football and Enron datasets like BINBALL and StarGen. This is likely because BINBALL and StarGen focus on airport transportation networks and therefore focus on modelling behavior like hub-spoke formations (Basu et al. 2015; Fügenschuh et al. 2018). These structures are more present in the sparser NELL-2 and Comm datasets than the denser Football and Enron datasets.

5.5 Classifier-based evaluation

TenGAN-CP performs fairly well on the Football dataset, with an accuracy of 0.70 and F1 score of 0.57 (recall that the lower the accuracy, the better). TenGAN-R performs well on the NELL-2 and Comm datasets. No model does a very good job of fooling the classifier on Enron, likely due to the higher number of views.

Most of the baselines do a poor job of fooling the classifier, with many baselines resulting in the classifier having 100% accuracy. One reason is because some generators are able to model some layers extremely well, but sometimes fail to model other layers. This leads to the classifier for certain layers to have very high accuracy, making the overall classifier very accurate. For example, BINBALL randomly assigns (based on a parameter p) a layer as a BA model or an ER model. This assignment can mean that the generated results for a given layer will be significantly different from those of the original graph, causing the classifier to be very accurate on that layer.

Another reason for the poor performance of the baselines is that the majority of them are statistical models and rely on general rules (e.g. preferential attachment for BA). While this may be able to mimic some attributes, the node and graph embeddings will likely greatly differ (except in the case where the original graphs exhibit simple structure).

5.6 Summary

TenGAN performs well on the majority of the datasets across all of the evaluation criteria. It performs especially well in the classifier-based and TenScore evaluations. This is likely because TenGAN learns directly from the data in contrast to most of the other baselines, which have to learn explicitly defined parameters instead. However, TenGAN-R does significantly worse than TenGAN-CP on most datasets, despite requiring more parameters. This is likely because TenGAN-R tends to have a hard time converging on the Football and Enron datasets. A possible reason for this is that the RESCAL decomposition imposes a stricter requirement on the factor matrix ${\textbf{A}}$ since it is shared across all layers, making it difficult for the model to learn well. The hyperparameter ${r}$ is also important in how well the model performs. Generally, ${r}$ has to be higher for sparser tensors and lower for denser tensors. We do not carefully tune ${r}$ in this paper—we select a resonable default (e.g., ${r}= 100$) and increase/decrease it until the model converges.

6 Related work

There have been several works on the topic of multiplex graph sampling. Interdonato et al. (2020) found that methods that work on standard graphs like Metropolis-Hastings random walks, BFS, and forest fire sampling (Leskovec and Faloutsos 2006) can also be applied to multiplex graphs. To improve random walk sampling on multiplex graphs, Gjoka et al. (2011) proposes union multigraph sampling—a method that uses the “union multigraph”, which consists of all edges across all views in the multiplex graph. Union multigraph sampling then performs a random walk over this multigraph to sample it. While unbiased samples are useful, we sometimes want a biased sample to better sample nodes with special properties. Khadangi et al. (2016) propose using learning automata to do so.

There has also been some previous work on multiplex graph generation. For example, Nicosia et al. (2013) propose a model to grow a multiplex graph based on traditional preferential attachment models like the Barabási-Albert (BA) model (Barabási and Albert 1999). BinBall (Basu et al. 2015) also builds upon the BA model and focuses on air transportation networks. StarGen (Fügenschuh et al. 2018) directly improves upon BinBall by using a per-layer edge count distribution and splitting the scaling factor of a new node into global and local factors.

Kim and Goh (2013) also uses single-layer preferential attachment models and tunes the correlation between layers. ANGEL (Fügenschuh et al. 2020) specifically tries to emulate the hub-and-spoke structure found in many graphs.

In recent years, neural networks have also been applied to graph generation. GraphRNN (You et al. 2018) uses a RNN to model graphs as a sequence of nodes of edges. NetGAN (Bojchevski et al. 2018) uses a LSTM to learn the distribution of biased random walks and reconstructs graphs from them. GraphVAE (Kipf and Welling 2016) uses a variational autoencoder to generate graphs. LGGAN (Fan and Huang 2019) generates the adjacency matrix directly, along with its associated labels. BRGAN (Shiao and Papalexakis 2021) generates rank-constrained graphs by first generating factor matrices, in a similar manner to TenGAN. There have also been several models for multi-scale graphs. The key difference between a multiplex and multi-scale graph is that a multiplex graph contains the same nodes with different edges in each view, while a multi-scale graph typically contains representations of the same underlying graph at different resolutions (different number of nodes) in each layer. Misc-GAN (Zhou et al. 2019) generates a multi-scale graph before collapsing it into a standard graph, and DMGNN (Li et al. 2020) predicts multi-scale graphs from previous ones.

To the best of our knowledge, there have been no other neural-network-based models for multiplex graph generation. HGEN (Ling et al. 2021) allows for the deep generation of heterogeneous networks by modelling random walks over the graph with a GAN. However, their approach largely focuses on the modelling of inter-layer edges with meta-paths. Heterogeneous networks refer to graphs with different node and edge types, while we focus on the case with shared nodes but different edges/views. We elaborate more on the precise definition of a multi-view graph in Sect. 2.1 above.

7 Conclusion

In this work, we discuss some of the issues associated with multiplex graph generation, as well as some solutions to those issues. One of these issues is the large number of parameters required to generate a multiplex graph using a neural network. We tackle this by proposing a novel GAN-based method that leverages the CPD and RESCAL decompositions to greatly reduce the number of parameters required.

Another issue with multiplex graph generation is a lack of evaluation criteria. We address this by proposing 3 different evaluation metrics that evaluate the realism of the graph along different aspects. We also modify HGEN, a model for heterogeneous networks, to work with multiplex graphs. We run our models on 4 different datasets, compare their results against HGEN and 3 other statistical multiplex generation models, and find that we perform better on the majority of them.