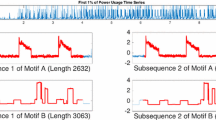
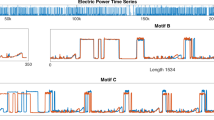
Abstract
In recent years, time series motif discovery has emerged as perhaps the most important primitive for many analytical tasks, including clustering, classification, rule discovery, segmentation, and summarization. In parallel, it has long been known that Dynamic Time Warping (DTW) is superior to other similarity measures such as Euclidean Distance under most settings. However, due to the computational complexity of both DTW and motif discovery, virtually no research efforts have been directed at combining these two ideas. The current best mechanisms to address their lethargy appear to be mutually incompatible. In this work, we present the first efficient, scalable and exact method to find time series motifs under DTW. Our method automatically performs the best trade-off of time-to-compute versus tightness-of-lower-bounds for a novel hierarchy of lower bounds that we introduce. As we shall show through extensive experiments, our algorithm prunes up to 99.99% of the DTW computations under realistic settings and is up to three to four orders of magnitude faster than the brute force search, and two orders of magnitude faster than the only other competitor algorithm. This allows us to discover DTW motifs in massive datasets for the first time. As we will show, in many domains, DTW-based motifs represent semantically meaningful conserved behavior that would escape our attention using all existing Euclidean distance-based methods.










































Similar content being viewed by others
Notes
In brief, the argument is this: Recall that cDTW is constrained by a parameter w, the maximum amount of warping allowed, and that as w approaches zero, cDTW degenerates to the Euclidean distance. It has been shown that the best setting for w decreases as the number of comparisons increase (see Fig. 6 of (Mueen et al. 2009)). For similarity search, there are \(O(n)\) comparisons, but for motif search there are \(O({n}^{2})\) comparisons, favoring a small value for w, perhaps approaching zero.
German for “time-giver”, Zeitgeber is normally only used for biological processes. Here we extend the meaning to social and cultural processes.
References
Alaee S (2020) Supporting website for this paper. https://sites.google.com/site/dtwmotifdiscovery/
Bagnall A, Lines J, Bostrom A, Large J, Keogh E (2017) The great time series classification bake off: a review and experimental evaluation of recent algorithmic advances. Data Min Knowl Disc 31(3):606–660
Bhattacharjee T, Song H, Lee G, Srinivasa SS (2018) Food manipulation: a cadence of haptic signals. arXiv preprint, arXiv:1804.08768
Chandola V, Banerjee A, Kumar V (2009) Anomaly detection: a survey. ACM Comput Surv (CSUR) 41(3):1–58
Chavarriaga R, Sagha H, Calatroni A, Digumarti ST, Tröster G, Millán JR, Roggen D (2013) The opportunity challenge: a benchmark database for on-body sensor-based activity recognition. Pattern Recogn Lett 34(15):2033–2042
Chiu B, Keogh E, Lonardi S (2003) Probabilistic discovery of time series motifs. In: Proceedings of the ninth ACM SIGKDD international conference on knowledge discovery and data mining, pp 493–498
Dua D, Graff C (2017) UCI machine learning repository
Dau HA, Keogh E (2017) Matrix profile v: a generic technique to incorporate domain knowledge into motif discovery. In: Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, pp 125–134
Dau HA, Bagnall A, Kamgar K, Yeh C-CM, Zhu Y, Gharghabi S, Ratanamahatana CA, Keogh E (2019) The UCR time series archive. IEEE/CAA J Autom Sin 6(6):1293–1305
Fang F, Shinozaki T (2018) Electrooculography-based continuous eye-writing recognition system for efficient assistive communication systems. PLoS ONE 13(2):e0192684
Feitosa RA, Rocha JM, Clodoaldo Ap ML, Peres SM (2018) Multidimensional representations for the gesture phase segmentation problem—an exploratory study using multilayer perceptrons. In: ICAART (2), pp 347–354
Geler Z, Kurbalija V, Ivanovic M, Radovanovic M, Dai W (2019) Dynamic time warping: Itakura vs Sakoe-Chiba. In: 2019 IEEE international symposium on innovations in intelligent systems and applications (INISTA). IEEE, pp 1–6
Gong X, Xiong Y, Huang W, Chen L, Lu Q, Hu Y (2015) Fast similarity search of multi-dimensional time series via segment rotation. In: International conference on database systems for advanced applications. Springer, Cham, pp 108–124
Imani S, Keogh E (2019) Matrix profile XIX: time series semantic motifs: a new primitive for finding higher-level structure in time series. In: 2019 IEEE international conference on data mining (ICDM). IEEE, pp 329–338
Junkui L, Yuanzhen W, Xinping L (2006) LB HUST: a symmetrical boundary distance for clustering time series. In: 9th international conference on information technology (ICIT'06). IEEE, pp 203–208
Keogh E, Lin J, Fu A (2005) Hot sax: efficiently finding the most unusual time series subsequence. In: Fifth IEEE international conference on data mining (ICDM'05). IEEE, pp 8-pp
Keogh E, Wei Li, Xi X, Vlachos M, Lee S-H, Protopapas P (2009) Supporting exact indexing of arbitrarily rotated shapes and periodic time series under euclidean and warping distance measures. VLDB J 18(3):611–630
Keogh E, Ratanamahatana CA (2005) Exact indexing of dynamic time warping. Knowl Inf Syst 7(3):358–386
Lagun D, Ageev M, Guo Q, Agichtein E (2014) Discovering common motifs in cursor movement data for improving web search. In: Proceedings of the 7th ACM international conference on web search and data mining, pp 183–192
Minnen D, Isbell CL, Essa I, Starner T (2007) Discovering multivariate motifs using subsequence density estimation and greedy mixture learning. In: Proceedings of the national conference on artificial intelligence, 1999, vol 22, no 1. MIT Press, Cambridge, MA, p 615
Mueen A, Keogh E, Zhu Q, Cash S, Westover B (2009) Exact discovery of time series motifs. In: Proceedings of the 2009 SIAM international conference on data mining. Society for Industrial and Applied Mathematics, pp 473–484
Murray D, Stankovic L, Stankovic V (2017) An electrical load measurements dataset of United Kingdom households from a two-year longitudinal study. Sci Data 4(1):1–12
Rabiner L (1993) Fundamentals of speech recognition. Prentice Hall, Upper Saddle River
Rakthanmanon T, Campana B, Mueen A, Batista G, Westover B, Zhu Q, Zakaria J, Keogh E (2013) Addressing big data time series: mining trillions of time series subsequences under dynamic time warping. ACM Trans Knowl Discov Data (TKDD) 7(3):1–31
Ratanamahatana CA, Keogh E (2005) Three myths about dynamic time warping data mining. In: Proceedings of the 2005 SIAM international conference on data mining. Society for Industrial and Applied Mathematics, pp 506–510
Sakoe H, Chiba S (1978) Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans Acoust Speech Signal Process 26(1):43–49
Salvador S, Chan P (2007) Toward accurate dynamic time warping in linear time and space. Intell Data Anal 11(5):561–580
Sankoff D (1983) Time warps, string edits, and macromolecules: the theory and practice of sequence comparison, reading. Cambridge University Press, Cambridge
Shokoohi-Yekta M, Wang J, Keogh E (2015) On the non-trivial generalization of dynamic time warping to the multi-dimensional case. In: Proceedings of the 2015 SIAM international conference on data mining. Society for Industrial and Applied Mathematics, pp 289–297
Silva DF, Batista GE (2018) Elastic time series motifs and discords. In: 2018 17th IEEE international conference on machine learning and applications (ICMLA). IEEE, pp 237–242
Silva DF, Batista GE, Keogh E (2016) Prefix and suffix invariant dynamic time warping. In: 2016 IEEE 16th international conference on data mining (ICDM). IEEE, pp 1209–1214
Tan CW, Petitjean F, Webb GI (2019) Elastic bands across the path: a new framework and method to lower bound DTW. In: Proceedings of the 2019 SIAM international conference on data mining. Society for Industrial and Applied Mathematics, pp 522–530
Tanaka Y, Iwamoto K, Uehara K (2005) Discovery of time-series motif from multi-dimensional data based on MDL principle. Mach Learn 58(2–3):269–300
Truong CD, Anh DT (2015) A fast method for motif discovery in large time series database under dynamic time warping. In: Nguyen VH, Le AC, Huynh VN (eds) Knowledge and systems engineering. Springer, Cham, pp 155–167
Willett DS, George J, Willett NS, Stelinski LL, Lapointe SL (2016) Machine learning for characterization of insect vector feeding. PLoS Comput Biol 12(11):e1005158
Wu R, Keogh EJ (2020) FastDTW is approximate and generally slower than the algorithm it approximates. arXiv preprint, arXiv:2003.11246
Yankov D, Keogh E, Rebbapragada U (2008) Disk aware discord discovery: finding unusual time series in terabyte sized datasets. Knowl Inf Syst 17(2):241–262
Yi B-K, Faloutsos C (2000) Fast time sequence indexing for arbitrary Lp norms
Zhu Y, Zimmerman Z, Senobari NS, Yeh C-CM, Funning G, Mueen A, Brisk P, Keogh E (2016) Matrix profile II: exploiting a novel algorithm and gpus to break the one hundred million barrier for time series motifs and joins. In: 2016 IEEE 16th international conference on data mining (ICDM). IEEE, pp 739–748
Zhu Y, Yeh C-CM, Zimmerman Z, Kamgar K, Keogh E (2018) Matrix profile XI: SCRIMP++: time series motif discovery at interactive speeds. In: 2018 IEEE international conference on data mining (ICDM). IEEE, pp 837–846
Zhu Y, Shasha D (2003) Warping indexes with envelope transforms for query by humming. In: Proceedings of the 2003 ACM SIGMOD international conference on management of data, pp 181–192
Ziehn A, Charfuelan M, Hemsen H, Markl V (2019) Time series similarity search for streaming data in distributed systems. In: EDBT/ICDT workshops
Acknowledgements
We thank all the creators of the data sets used in this work.
Funding
Funding was provided by National Science Foundation (Grant No. 1631776)
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible editor: Johannes Fürnkranz.
Appendix
Appendix
1.1 Reproducibility
We have taken extraordinary steps to make sure that every experiment (including the figures and samples that proceed the official experimental section) are easy to reproduce. To this end:
-
For experiments that have a stochastic element, we initialize with the same random number generator seed before each iteration. This ensures that a reader can exactly reproduce our output, independent of their platform.
-
Every data used in each figure or table is explicitly labeled with the name of the figure/table and archived at Alaee (2020) in a universally readable ASCII plain text format, in addition to the.mat format that we use internally.
-
We have created a presentation that gives additional information about anything we did to create our final figures. For example, purely for aesthetic reasons, we “flipped” one of the dendrograms shown in Fig. 3 upside down (without changing its topology or distances). The presentation reconciles the slight differences between the output of the code, and the final figures.
-
In addition to the main code, we have included all the minor code, including the code to produce dendrograms, etc.
For many experiments we choose to use time series and query lengths that are powers of two. This is not required for SWAMP but is a consideration for future researchers who may try to improve on our results with either DFT or DWT methods, both of which have their best cases when the data lengths are powers of two.
As noted in the paper but reiterated here, in many works, the size of the warping window is often given as a percentage of the length of the time series (Keogh and Ratanamahatana 2005; Ratanamahatana and Keogh 2005), in this work we give it as an absolute number. One reason for this is because a given percentage may not evenly divide a time series length, and different rounding policies may affect the results.
Where warranted, we presented some details in the paper very tersely. For example, we noted in the main text:
Finally, we compared to Silva and Batista (2018), which is the only other exact algorithm for finding DTW motifs. On the three datasets above this algorithm was 17,274%, 185,511% and 13,857% respectively.
The details are a little sparse in that text. However:
-
The differences are so large that we hope the reader will understand our decision not to spend too much of the page limits here.
-
The full detailed results are available at Alaee (2020), together with the full code and data needed to reproduce the results.
Here we note that this comparison was completely fair. We used the exact same computer, same datasets, and same implementations of all common subroutines, including the various lower bounds, ED and DTW comparison algorithms, etc. Moreover, we further optimized the original algorithm extensively. The original algorithm finds both discords and motifs under DTW, but we made it faster by removing the need to find discords, and only requiring it to find the top-1 motif.
Likewise, our comparison to brute-force search was rigorously fair. There are many ways to make a DTW-based algorithm perform poorly. For example, one could implement the rival method using the recursive version of DTW instead of the iterative version. The recursive version of DTW is one to two orders of magnitude slower than the iterative version. However, here we again used the exact same computer, same datasets, and most importantly same implementations of all common subroutines, including the various lower bounds, ED and DTW comparison algorithms.
1.1.1 A reproducibility “ROSETTA STONE”
As noted above, we have made all our code publicly available in perpetuity (Alaee 2020). However, a reader may wish to implement and test our ideas on another platform. If we both agree on all distance measures, including the Euclidean distance, cDTW distance and parametrized lower bounds, then we can be virtually assured that all other steps will be in agreement. It may seem unlikely that we could disagree on such matters. However, our experience suggests otherwise. For example, we have seen the w parameter in cDTW interpreted as the total freedom to wander off the diagonal. In essence, that (mis)understanding will give only half the w value that we mean to communicate (and is more commonly understood (Rakthanmanon et al. 2013)). Likewise, by default, some DTW programs normalize the distance by the path length. This makes only a very subtle difference when w is small, nevertheless it could cause our lower bounds to no longer be admissible. Thus, in order to make sure we agree on all measures, in Table 5 we will create a pair of time series that the interested reader can literally cut-and-paste into their framework and compare results on all measures.
Note that after we z-normalized these time series, we rounded them to have just two significant digits, in order to further facilitate a detailed forensic tracing of the computation. However, this rounding means that the two time series are no longer exactly z-normalized. All subsequent analysis assumes the exact values in Table 5.
In Fig. 43 we show a visual intuition for the various measures that are key to this work. The Euclidean distance ED(Q,T) is 7.88098.
(Top to bottom) For the two time series listed in Table 1, a visual intuition that shows: the Euclidean distance, the cDTW, the classic LBKeogh lower bound, and the reduced dimensionality LBKeogh lower bound
Recall that in our implementation we perform the optimization of not using the squared root function (see Sect. 4.1.1 of Rakthanmanon et al. 2013). However, we ignore that optimization here. Using a value of eight for the warping parameter w, cDTW(Q,T) is 2.4240. The value of Keogh’s classic lower bound, in our notation LBKeogh1:1(Q,T), is 1.5865. It is important to recall that this function is not symmetric, in general LBKeogh1:1(Q,T) ≠ LBKeogh1:1(T,Q). Finally, Fig. 43.bottom illustrates the four-fold reduced lower bound, LBKeogh4:1(Q,T), which has a value of 0.4999.
Note that LBKeogh4:1(Q,T) ≤ LBKeogh1:1(Q,T) ≤ cDTW(Q,T) ≤ ED(Q,T) as we should expect.
Rights and permissions
About this article
Cite this article
Alaee, S., Mercer, R., Kamgar, K. et al. Time series motifs discovery under DTW allows more robust discovery of conserved structure. Data Min Knowl Disc 35, 863–910 (2021). https://doi.org/10.1007/s10618-021-00740-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10618-021-00740-0