Skip to main content
SpringerLink
Log in

Kernel mixture model for probability density estimation in Bayesian classifiers

  • Published:
Data Mining and Knowledge Discovery Aims and scope Submit manuscript

Abstract

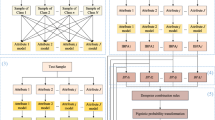
Estimating reliable class-conditional probability is the prerequisite to implement Bayesian classifiers, and how to estimate the probability density functions (PDFs) is also a fundamental problem for other probabilistic induction algorithms. The finite mixture model (FMM) is able to represent arbitrary complex PDFs by using a mixture of mutimodal distributions, but it assumes that the component mixtures follows a given distribution, which may not be satisfied for real world data. This paper presents a non-parametric kernel mixture model (KMM) based probability density estimation approach, in which the data sample of a class is assumed to be drawn by several unknown independent hidden subclasses. Unlike traditional FMM schemes, we simply use the k-means clustering algorithm to partition the data sample into several independent components, and the regional density diversities of components are combined using the Bayes theorem. On the basis of the proposed kernel mixture model, we present a three-step Bayesian classifier, which includes partitioning, structure learning, and PDF estimation. Experimental results show that KMM is able to improve the quality of estimated PDFs of conventional kernel density estimation (KDE) method, and also show that KMM-based Bayesian classifiers outperforms existing Gaussian, GMM, and KDE-based Bayesian classifiers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  • Babich GA, Camps OI (1996) Weighted parzen windows for pattern classification. IEEE Trans Pattern Anal Mach Intell 18(5):567–570

    Article  Google Scholar 

  • Bielza C (2014) Discrete bayesian network classifiers: a survey. ACM Comput Surv 47(1):1–43

    Article  MathSciNet  MATH  Google Scholar 

  • Bouckaert RR (2004) Naive bayes classifiers that perform well with continuous variables. In: AI 2004: advances in artificial intelligence, Springer, Berlin, pp 1089–1094

  • Castillo E, Gutierrez JM, Hadi AS (2012) Expert systems and probabilistic network models. Springer, Berlin

    MATH  Google Scholar 

  • Chickering DM (2010) Learning bayesian networks is np-complete. Lect. Notes Stat. 112(2):121–130

    MathSciNet  Google Scholar 

  • Chow CK, Liu CN, Liu c (1968) Approximating discrete probability distributions with dependence trees. IEEE Trans. Inf. Theory 14(3):462–467 IEEE Transactions on Information Theory 14(3), 462–467

    Article  MATH  Google Scholar 

  • Dehnad K (1986) Density estimation for statistics and data analysis. Chapman and Hall, Boca Raton

    Google Scholar 

  • Domingos P, Pazzani M (1997) On the optimality of the simple bayesian classifier under zero-one loss. Mach Learn 29(2–3):103–130

    Article  MATH  Google Scholar 

  • Duda RO, Hart PE, Stork DG (2012) Pattern classification. Wiley, New York

    MATH  Google Scholar 

  • Escobar MD, West M (1995) Bayesian density estimation and inference using mixtures. J Am Stat Assoc 90(430):577–588

    Article  MathSciNet  MATH  Google Scholar 

  • Figueiredo MAT, Jain AK (2002) Unsupervised learning of finite mixture models. IEEE Trans Pattern Anal Mach Intell 24(3):381–396

    Article  Google Scholar 

  • Friedman N, Dan G, Goldszmidt M (1997) Bayesian network classifiers. Mach Learn 29(2–3):131–163

    Article  MATH  Google Scholar 

  • Girolami M, He C (2003) Probability density estimation from optimally condensed data samples. IEEE Trans Pattern Anal Mach Intell 25(10):1253–1264

    Article  Google Scholar 

  • Hand DJ, Till RJ (2001) A simple generalisation of the area under the roc curve for multiple class classification problems. Mach Learn 45(2):171–186

    Article  MATH  Google Scholar 

  • Hand DJ, Yu K (2001) Idiot’s bayesłnot so stupid after all? Int Stat Rev 69(3):385–398

    MATH  Google Scholar 

  • Heckerman D, Dan G, Chickering DM (1995) Learning bayesian networks: the combination of knowledge and statistical data. Mach Learn 20(3):197–243

    MATH  Google Scholar 

  • Heidenreich NB, Schindler A, Sperlich S (2010) Bandwidth selection methods for kernel density estimation—a review of performance. Social Science Electronic Publishing, Rochester

    Google Scholar 

  • Holmström L (2000) The accuracy and the computational complexity of a multivariate binned kernel density estimator. J Multivar Anal 72(2):264–309

    Article  MathSciNet  MATH  Google Scholar 

  • Holmström L, Hämäläinen A (1993) The self-organizing reduced kernel density estimator. In: IEEE international conference on neural networks, IEEE, pp 417–421

  • Jeon B, Landgrebe DA (1994) Fast parzen density estimation using clustering-based branch and bound. IEEE Trans Pattern Anal Mach Intell 16(9):950–954

    Article  Google Scholar 

  • Jeon J, Taylor JW (2012) Using conditional kernel density estimation for wind power density forecasting. J Am Stat Assoc 107(497):66–79

    Article  MathSciNet  MATH  Google Scholar 

  • Jiang L, Cai Z, Wang D, Zhang H (2012) Improving tree augmented naive bayes for class probability estimation. Knowl-Based Syst 26:239–245

    Article  Google Scholar 

  • John GH, Langley P (2013) Estimating continuous distributions in bayesian classifiers. In: Proceedings of the eleventh conference on Uncertainty in artificial intelligence, pp 338–345

  • Kayabol K, Zerubia J (2013) Unsupervised amplitude and texture classification of sar images with multinomial latent model. IEEE Trans Image Process 22(2):561–572

    Article  MathSciNet  MATH  Google Scholar 

  • Leray P, Francois O (2004) BNT structure learning package: documentation and experiments. Technical Report FRE CNRS 2645, Laboratoire PSI, Universite et INSA de Rouen

  • Pérez A, Larrañaga P, Inza I (2009) Bayesian classifiers based on kernel density estimation: flexible classifiers. Int J Approx Reason 50(2):341–362

    Article  MATH  Google Scholar 

  • Raykar VC, Duraiswami R (2006) Fast optimal bandwidth selection for kernel density estimation. In: SIAM international conference on data mining, April 20–22, Bethesda, MD, USA

  • Reynolds DA, Rose RC (1995) Robust text-independent speaker identification using gaussian mixture speaker models. IEEE Trans Speech Audio Process 3(1):72–83

    Article  Google Scholar 

  • Rish I (2001) An empirical study of the naive bayes classifier. J Univ Comput Sci 1(2):127

    Google Scholar 

  • Schwander O, Nielsen F (2012) Model centroids for the simplification of kernel density estimators. In: IEEE international conference on acoustics, speech and signal processing, pp 737–740

  • Schwander O, Nielsen F (2013) Learning mixtures by simplifying kernel density estimators. Matrix Information Geometry. Springer, Berlin, pp 403–426

    MATH  Google Scholar 

  • Scott DW (2015) Multivariate density estimation: theory, practice, and visualization. Wiley, New York

    Book  MATH  Google Scholar 

  • Scott DW, Sheather SJ (1985) Kernel density estimation with binned data. Commun Stat Theory Methods 14(6):1353–1359

    Article  Google Scholar 

  • Shen W, Tokdar ST, Ghosal S (2013) Adaptive bayesian multivariate density estimation with dirichlet mixtures. Biometrika 100(3):623–640

    Article  MathSciNet  MATH  Google Scholar 

  • Simonoff JS (1997) Smoothing methods in statistics. Technometrics 92(3):338–339

    MathSciNet  MATH  Google Scholar 

  • Sucar LE (2015) Bayesian classifiers. Springer, London

    Book  Google Scholar 

  • Topchy AP, Jain AK, Punch WF (2004) A mixture model for clustering ensembles. In: SDM, SIAM, pp 379–390

  • Wang F, Zhang C, Lu N (2005) Boosting GMM and its two applications. In: International workshop on multiple classifier systems, vol 3541. Springer, Berlin, Heidelberg, pp 12–21

  • Wang S, Wang J, Chung FL (2013) Kernel density estimation, kernel methods, and fast learning in large data sets. IEEE Trans Cybern 44(1):1–20

    Article  Google Scholar 

  • Xiong F, Liu Y, Cheng J (2017a) Modeling and predicting opinion formation with trust propagation in online social networks. Commun Nonlinear Sci Numer Simul 44:513–524

    Article  MathSciNet  Google Scholar 

  • Xiong F, Liu Y, Wang L, Wang X (2017b) Analysis and application of opinion model with multiple topic interactions. Chaos 27(8):083,113

    Article  MathSciNet  Google Scholar 

  • Xu X, Yan Z, Xu S (2015) Estimating wind speed probability distribution by diffusion-based kernel density method. Electr Power Syst Res 121:28–37

    Article  Google Scholar 

  • Yang Y, Webb GI (2009) Discretization for naive-bayes learning: managing discretization bias and variance. Mach Learn 74(1):39–74

    Article  Google Scholar 

  • Yin H, Allinson NM (2001) Self-organizing mixture networks for probability density estimation. IEEE Trans Neural Netw 12(2):405–411

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by National Natural Science Foundation of China under Grant 61772064, and Academic Discipline, Post-Graduate Education Project of the Beijing Municipal Commission of Education, and Fundamental Research Funds for the Central Universities under Grant 2017YJS026. The authors also thanks the anonymous reviewers’ valuable comments and suggestions for improving the quality of this paper.

Author information

Authors and Affiliations

  1. School of Electronic and Information Engineering, Key Laboratory of Communication and Information Systems, Beijing Municipal Commission of Education, Beijing Jiaotong University, Beijing, 100044, China

    Wenyu Zhang & Zhenjiang Zhang

  2. School of Information Science and Engineering, Fujian University of Technology, Fuzhou, 350118, China

    Han-Chieh Chao

  3. School of Mathematics and Computer Science, Wuhan Polytechnic University, Wuhan, 430023, China

    Han-Chieh Chao

  4. Department of Electrical Engineering, National Dong Hwa University, Hualien, 974, Taiwan

    Han-Chieh Chao

  5. Department of Computer Science and Information Engineering, National Ilan University, Yilan, 260, Taiwan

    Han-Chieh Chao

  6. Department of Technology Application and Human Resource Development, National Taiwan Normal University, Taipei, 106, Taiwan

    Fan-Hsun Tseng

Authors
  1. Wenyu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhenjiang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Han-Chieh Chao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Fan-Hsun Tseng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhenjiang Zhang.

Additional information

Responsible editor: Fei Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, W., Zhang, Z., Chao, HC. et al. Kernel mixture model for probability density estimation in Bayesian classifiers. Data Min Knowl Disc 32, 675–707 (2018). https://doi.org/10.1007/s10618-018-0550-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10618-018-0550-5

Keywords

Search

Navigation