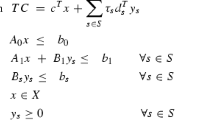Skip to main content
SpringerLink
Log in

A Benders Decomposition Method for Solving Stochastic Complementarity Problems with an Application in Energy

  • Published:
Computational Economics Aims and scope Submit manuscript

Abstract

In this paper we present a new Benders decomposition method for solving stochastic complementarity problems based on the work by Fuller and Chung (Comput Econ 25:303–326, 2005; Eur J Oper Res 185(1):76–91, 2007). A master and subproblem are proposed both of which are in the form of a complementarity problem or an equivalent variational inequality. These problems are solved iteratively until a certain convergence gap is sufficiently close to zero. The details of the method are presented as well as an extension of the theory from Fuller and Chung (2005, 2007). In addition, extensive numerical results are provided based on an electric power market model of Hobbs (IEEE Trans Power Syst 16(2):194–202, 2001) but for which stochastic elements have been added. These results validate the approach and indicate dramatic improvements in solution times as compared to solving the extensive form of the problem directly.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Ahn B. H., Hogan W. W. (1982) On convergence of the PIES algorithm for computing equilibria. Operations Research 30(2): 281–300

    Article  Google Scholar 

  • Belknap, M. H., Chen, C. H., & Harker, P. T. (2000). A gradient-based method for analyzing stochastic variational inequalities with one uncertain parameter. OPIM Working Paper 00-03-13. Department of Operations and Information Management, Wharton School, March.

  • Benders J. F. (1962) Partitioning procedures for solving mixed-variables programming problems. Numerische Mathematik 4: 238–252

    Article  Google Scholar 

  • Birge J. R., Louveaux F. (1997) Introduction to stochastic programming. Springer, New York

    Google Scholar 

  • Brooke, A., Kendrick, D., Meeraus, A., & Raman, R. (2008). GAMS—a user’s guide. GAMS Development Corporation, Washington, DC. http://www.gams.com/docs/document.htm.

  • Cabero, J., Baillo, A., Cerisola, S., & Ventosa, M. (2005a). Electricity market equilibrium model with risk constraints via Benders decomposition. In INFORMS annual conference, San Francisco, November.

  • Cabero, J., Baillo, A., Ventosa, M., & Cerisola, S. (2005b). Application of Benders decomposition to an equilibrium problem. In 15th PSCC, Liege, August.

  • Chen Y., Hobbs B. F. (2005) An oligopolistic power market model with tradable Nox permits. IEEE Transactions on Power Systems 20(1): 119–129

    Article  Google Scholar 

  • Dantzig G., Wolfe P. (1961) The decomposition algorithm for linear programs. Econometrica 29(4): 767–778

    Article  Google Scholar 

  • De Wolf D., Smeers Y. (1997) A stochastic version of a Stackelberg–Nash–Cournot equilibrium model. Management Science 43(2): 190–197

    Article  Google Scholar 

  • Dupačová J., Grőwe-Kuska N., Rőmisch W. (2003) Scenario reduction in stochastic programming. Mathematical Programming 93(3): 493–511

    Article  Google Scholar 

  • Egging R., Gabriel S. A. (2006) Examining market power in the European natural gas market. Energy Policy 34(17): 2762–2778

    Article  Google Scholar 

  • Egging R., Gabriel S. A., Holz F., Zhuang J. (2008) A complementarity model for the European natural gas market. Energy Policy 36: 2385–2414

    Article  Google Scholar 

  • Facchinei F., Pang J.-S. (2003) Finite-dimensional variational inequalities and complementarity problems. Springer, New York

    Google Scholar 

  • Ferris, M. C., & Munson, T. S. (2005). PATH 4.6. GAMS Development Corporation, Washington, DC. http://www.gams.com/docs/document.htm.

  • Fuller J. D., Chung W. (2005) Dantzig–Wolfe decomposition of variational inequalities. Computational Economics 25: 303–326

    Article  Google Scholar 

  • Fuller J. D., Chung W. (2007) Benders decomposition for a class of variational inequalities. European Journal of Operational Research 185(1): 76–91

    Article  Google Scholar 

  • Gabriel, S. A., & Fuller, J. D. (2008). A Benders method for solving stochastic complementarity problems with an application in energy. In CORS/optimization days joint conference, Quebec City, May.

  • Gabriel S. A., Kiet S., Zhuang J. (2005a) A mixed complementarity-based equilibrium model of natural gas markets. Operations Research 53(5): 799–818

    Article  Google Scholar 

  • Gabriel S. A., Zhuang J., Egging R. (2009) Solving stochastic complementarity problems in energy market modeling using scenario reduction. European Journal of Operational Research 197(3): 1028–1040

    Article  Google Scholar 

  • Gabriel S. A., Zhuang J., Kiet S. (2005b) A large-scale complementarity model of the North American natural gas market. Energy Economics 27: 639–665

    Article  Google Scholar 

  • García-Bertrand R., Conejo A. J., Gabriel S. A. (2006) Electricity market near-equilibrium under locational marginal pricing and minimum profit conditions. European Journal of Operational Research 174: 457–479

    Article  Google Scholar 

  • Genc T. S., Reynolds S. S., Sen S. (2007) Dynamic oligopolistic games under uncertainty: A stochastic programming approach. Journal of Economic Dynamics and Control 31(1): 55–80

    Article  Google Scholar 

  • Global Competition Review. (2003). Gas regulation in 26 jurisdictions worldwide. http://www.globalcompetitionreview.com.

  • Gröwe-Kuska, N., Heitsch, H., & Römisch, W. (2003). Scenario reduction and scenario tree construction for power management problems. In A. Borghetti, C. A. Nucci, & M. Paolone (Eds.), IEEE Bologna Power tech proceedings.

  • Gürkan G., Özge A. Y., Robinson S. M. (1999) Sample-path solution of stochastic variational inequalities. Mathematical Programming 84: 313–333

    Article  Google Scholar 

  • Haurie A., Moresino F. (2002) S-Adapted oligopoly equilibria and approximations in stochastic variational inequalities. Annals of Operations Research 114: 183–201

    Article  Google Scholar 

  • Haurie, A. & Zaccour, G. (2005). S-Adapted equilibria in games played over event trees: An overview. In A.S. Nowak et al. (Eds.), Advances in dynamic games. Annals of the International Society of Dynamic Games, 7, 417–444.

  • Haurie, A., Zaccour, G., Legrand, J., & Smeers, Y. (1987). A stochastic dynamic Nash–Cournot model for the European gas market. Technical Report G-86-24, GERAD, Ecole des Hautes Etudes Commerciales, Montréal, Québec, Canada.

  • Heitsch H., Römisch W. (2003) Scenario reduction algorithms in stochastic programming. Computational Optimization and Applications 24: 187–206

    Article  Google Scholar 

  • Hobbs B. F. (2001) Linear complementarity models of Nash–Cournot competition in bilateral and POOLCO power markets. IEEE Transactions on Power Systems 16(2): 194–202

    Article  Google Scholar 

  • Metzler C., Hobbs B. F., Pang J.-S. (2003) Nash–Cournot equilibria in power markets on a linearized DC network with arbitrage: Formulations and properties. Networks & Spatial Economics 3(2): 123–150

    Article  Google Scholar 

  • Nocedal J., Wright S. J. (1999) Numerical optimization. Springer, New York

    Book  Google Scholar 

  • Römisch, W., Dupačová, J., Gröwe-Kuska, N., & Heitsch, H. (2003). Approximations of stochastic programs. Scenario tree reduction and construction. GAMS Workshop, Heidelberg, September 1–3, Berlin: DFG Research Center.

  • Shanbhag, U., Glynn, P., & Infanger, G. (2005). A complementarity framework for forward contracting under uncertainty. In INFORMS annual conference, San Francisco, November.

  • Shanbhag, U., Infanger, G., & Glynn, P. (2008). A complementarity framework for forward contracting under uncertainty (under review).

  • Waller, S. T. (2000). Optimization and control of stochastic dynamic transportation systems: Formulations, solution methodologies, and computational experience. Ph.D. Dissertation, Northwestern University, Chicago.

  • Yao J., Adler I., Oren S.S. (2008) Modeling and computing two-settlement oligopolistic equilibrium in a congested electricity network. Operations Research 56(1): 34–47

    Article  Google Scholar 

  • Zhuang J., Gabriel S. A. (2008) A complementarity model for solving stochastic natural gas market equilibria. Energy Economics 30(1): 113–147

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil and Environmental Engineering, University of Maryland, 1143 Glenn L. Martin Hall, College Park, MD, 20742-3021, USA

    S. A. Gabriel

  2. Department of Management Sciences, Faculty of Engineering, University of Waterloo, 200 University Avenue West, Waterloo, ON, N2L 3G1, Canada

    J. D. Fuller

Authors
  1. S. A. Gabriel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. D. Fuller
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. D. Fuller.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gabriel, S.A., Fuller, J.D. A Benders Decomposition Method for Solving Stochastic Complementarity Problems with an Application in Energy. Comput Econ 35, 301–329 (2010). https://doi.org/10.1007/s10614-010-9200-8

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10614-010-9200-8

Keywords

Search

Navigation