Skip to main content
SpringerLink
Log in

Asymptotic Behavior of Regularized Solutions of One Model of Economic Growth with Delay

  • II. MATHEMATICAL MODELING
  • Published:
Computational Mathematics and Modeling Aims and scope Submit manuscript

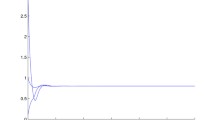
We consider an ill-posed problem to find the solutions of an economic growth model with a delay. Asymptotic formulas are constructed for regularized solutions of the delayed system on a finite interval on the negative half-axis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Murray, Nonlinear Differential Equations in Biology [Russian translation], Mir, Moscow (1983).

    Google Scholar 

  2. K. C. Velupillai and N. Dharmaraj, The Time-to-Build Tradition in Business Cycle Modelling, ASSRU Discussion Paper 09–11, Trento (March 2011).

    Google Scholar 

  3. S. Ruan, “On nonlinear dynamics of predator-prey models with discrete delay,” Math. Model. Nat. Phenom., 4, No. 2, 140–188 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  4. J. Maynard-Smith, Models in Ecology [Russian translation], Mir, Moscow (1976).

    Google Scholar 

  5. R. M. Goodwin, “A growth cycle,” in: Socialism, Capitalism and Economic Growth, Cambridge Univ. Press (1967).

    Google Scholar 

  6. V. Volterra, Mathematical Theory of the Struggle for Survival [Russian translation], Nauka, Moscow (1976).

    Google Scholar 

  7. Report on the State and Preservation of the Environment in Vologda Province in 2006 [in Russian], Vologda Provincial Government, Department of Natural Resources and Preservation of the Environment of the Vologda Province, Vologda (2007).

  8. A. Yu. Kolesov and Yu. S. Kolesov, “Relaxation oscillations in mathematical models in ecology,” Trudy Mat. Inst. im. V. A. Steklov, Vol. 199 (1993).

  9. A. N. Tikhonov and V. Ya. Arsenin, Methods of Solution of Ill-Posed Problems [in Russian], Nauka, Moscow 1986.

    Google Scholar 

  10. Yu. F. Dolgii and P. G. Surkov, “Ill-posed problem of reconstruction of the population size in Hutchinsons mathematical model,” Trudy Inst. Matem. Mekhan. UrORAN, 17, No. 1, 70–84 (2011).

    Google Scholar 

  11. M. M. Vainberg, Variational Method and the Method of Monotone Operators [in Russian], Nauka, Moscow (1972).

    Google Scholar 

  12. Rapoport, On Some Asymptotic Methods for Ordinary Differential Equations [in Russian], Nauka, Moscow (1953).

    Google Scholar 

  13. J. Hale, Theory of Functional Differential Equations [Russian translation], Mir (1984).

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics and Mechanics, Ural Branch of the Russian Academy of Science, Ekaterinburg, Russia

    P. G. Surkov

Authors
  1. P. G. Surkov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. G. Surkov.

Additional information

Translated from Prikladnaya Matematika i Informatika, No. 44, 2013, pp. 50–65.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Surkov, P.G. Asymptotic Behavior of Regularized Solutions of One Model of Economic Growth with Delay. Comput Math Model 25, 484–499 (2014). https://doi.org/10.1007/s10598-014-9243-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10598-014-9243-0

Keywords

Search

Navigation