Skip to main content
SpringerLink
Log in

Mathematical model of fuel layer degradation when the laser target is heated by thermal radiation in the reactor working chamber

  • Mathematical Modeling
  • Published:
Computational Mathematics and Modeling Aims and scope Submit manuscript

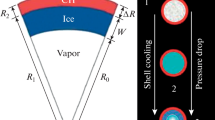
We propose a mathematical model of the changes occurring in the geometrical properties of the deuterium–tritium layer on the laser target in the process of its insertion into the reactor working chamber. The model is a parabolic equation of general form in spherical coordinates with nonlinear boundary conditions on a moving boundary. We show that under physically justified assumptions this problem may be regarded as a Stefan problem for a singularly perturbed parabolic equation. The first terms of the solution series are written out. Numerical calculations of the fuel layer degradation time are presented for a real target.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. A. Belolipetskii, “A singularly perturbed Stefan problem describing fuel layer degradation in a laser target,” Vestnik MGU, ser. 15, Vychisl. Matem. Kibern., No. 1, 10 –18 (2008).

  2. A. A. Belolipetskii, “Modeling complex physical systems,” in: Proc. 2nd Russian Sci. Conf. on Mathematical Modeling of Developing Economics ECOMOD-2007, Kirov, 9 –15 July 2007 [in Russian], (2007), pp. 37– 48.

  3. I. V. Aleksandrova, A. A. Belolipetskii, E. R. Koresheva, and others, “Preserving the parameters of a cryogenic target in the process of insertion into the thermonuclear combustion zone,” Voprosy Atomnoi Nauki i Tekhniki, No. 3, 27– 47 (2007).

  4. R. Siegel and J. Howell, Thermal Radiation Heat Transfer [Russian translation], Mir, Moscow (1975).

    Google Scholar 

  5. L. G. Loitsyanskii, Fluid and Gas Dynamics [in Russian], Nauka, Moscow (1970).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Computational Mathematics and Cybernetics, Moscow State University, Moscow, Russia

    A. A. Belolipetskii, E. A. Malinina & K. O. Semenov

Authors
  1. A. A. Belolipetskii
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. A. Malinina
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. O. Semenov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. A. Belolipetskii.

Additional information

Translated from Prikladnaya Matematika i Informatika, No. 32, pp. 5–19, 2009.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Belolipetskii, A.A., Malinina, E.A. & Semenov, K.O. Mathematical model of fuel layer degradation when the laser target is heated by thermal radiation in the reactor working chamber. Comput Math Model 21, 1–17 (2010). https://doi.org/10.1007/s10598-010-9050-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10598-010-9050-1

Keywords

Search

Navigation