Abstract
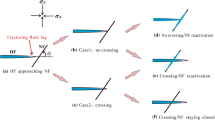
In this paper, we apply the enhanced local pressure (ELP) model to study crack interaction in hydraulic fracturing. The method is based on the extended finite element method (X-FEM) where the pressure and the displacement fields are assumed to be discontinuous over the fracture exploiting the partition of unity property of finite element shape functions. The material is fully saturated and Darcy’s law describes the fluid flow in the material. The fracture process is described by a cohesive traction-separation law, whereas the pressure in the fracture is included by an additional degree of freedom. Interaction of a hydraulic fracture with a natural fracture is considered by assuming multiple discontinuities in the domain. The model is able to capture several processes, such as fracture arrest on the natural fracture, or hydraulic fractures that cross the natural fracture. Fluid is able to flow from the hydraulic fracture into the natural fracture. Two numerical criteria are implemented to determine whether or not the fracture is crossing or if fluid diversion occurs. Computational results showing the performance of the model and the effectiveness of the two criteria are presented. The influence of the angle between a hydraulic fracture and a natural fracture on the interaction behaviour is compared with experimental results and theoretical data.
Article PDF
Similar content being viewed by others
References
Smith, M.B., Montgomery, C.: Hydraulic fracturing. CRC Press, Boca Raton (2015)
McClure, M., Horne, R.N.: The potential effect of network complexity on recovery of injected fluid following hydraulic fracturing. In: SPE unconventional resources conference. society of petroleum engineers (2014)
Maxwell, S.C., Urbancic, T.I., Steinsberger, N., Zinno, R.: Microseismic imaging of hydraulic fracture complexity in the barnett shale. In: SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers (2002)
Lee, H.P., Olson, J.E., Holder, J., Gale, J.F.W., Myers, R.D.: The interaction of propagating opening mode fractures with preexisting discontinuities in shale. J. Geophys. Res. Solid Earth 120(1), 169–181 (2015)
Blanton, T.L.: An experimental study of interaction between hydraulically induced and pre-existing fractures. In: SPE unconventional gas recovery symposium. Society of Petroleum Engineers (1982)
Zhou, J., Chen, M., Jin, Y., Zhang, G.: Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 45(7), 1143–1152 (2008)
Renshaw, C.E., Pollard, D.D.: An experimentally verified criterion for propagation across unbounded frictional interfaces in brittle, linear elastic materials. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr. 32, 237–249 (1995)
Gu, H., Weng, X., Lund, J.B., Mack, M.G., Ganguly, U., Suarez-Rivera, R.: Hydraulic fracture crossing natural fracture at nonorthogonal angles: a criterion and its validation. SPE Prod Oper 27(01), 20–26 (2012)
Freund, L.B.: Dynamic fracture mechanics. Cambridge University Press, Cambridge (1998)
Xu, X.P., Needleman, A.: Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 42(9), 1397–1434 (1994)
Valko, P., Economides, M.J.: Hydraulic fracture mechanics. Wiley, New York (1995)
Belytschko, T., Black, T.: Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 45(5), 601–620 (1999)
Melenk, J.M., Babuṡka, I.: The partition of unity finite element method: basic theory and applications. Comput. Methods Appl. Mech. Eng. 139(1), 289–314 (1996)
Moës, N., Dolbow, J., Belytschko, T.: A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 46(1), 131–150 (1999)
Daux, C., Moës, N., Dolbow, J., Sukumar, N., Belytschko, T.: Arbitrary branched and intersecting cracks with the extended finite element method. Int. J. Numer. Methods Eng. 48(12), 1741–1760 (2000)
Dahi-Taleghani, A., Olson, J.E.: Numerical modeling of multistranded-hydraulic-fracture propagation: Accounting for the interaction between induced and natural fractures. SPE J. 16(3), 575–581 (2011)
Khoei, A.R., Vahab, M., Hirmand, M.: Modeling the interaction between fluid-driven fracture and natural fault using an enriched-fem technique. Int. J. Fract. 197(1), 1–24 (2016)
de Borst, R, Réthoré, J., Abellan, M.A.: A numerical approach for arbitrary cracks in a fluid-saturated medium. Arch. Appl. Mech. 75(10), 595–606 (2006)
Mohammadnejad, T., Khoei, A.R.: Hydro-mechanical modeling of cohesive crack propagation in multiphase porous media using the extended finite element method. Int. J. Numer. Anal. Methods Geomech. 37(10), 1247–1279 (2012)
Remij, E.W., Remmers, J.J.C., Pizzocolo, F., Smeulders, D.M.J., Huyghe, J.M.: A partition of unity-based model for crack nucleation and propagation in porous media, including orthotropic materials. Transp. Porous Media 106(3), 505–522 (2015)
Mohammadnejad, T., Khoei, A.R.: An extended finite element method for hydraulic fracture propagation in deformable porous media with the cohesive crack model. Finite Elem. Anal. Des. 73, 77–95 (2013)
Formaggia, L., Fumagalli, A., Scotti, A., Ruffo, P.: A reduced model for darcy’s problem in networks of fractures. ESAIM: Math. Model. Numer. Anal. 48(4), 1089–1116 (2014)
Flemisch, B., Fumagalli, A., Scotti, A.: A review of the xfem-based approximation of flow in fractured porous media. In: Advances in Discretization Methods, pages 47–76. Springer (2016)
Carrier, B., Granet, S.: Numerical modeling of hydraulic fracture problem in permeable medium using cohesive zone model. Eng. Fract. Mech. 79, 312–328 (2012)
Secchi, S., Schrefler, B.A.: A method for 3D hydraulic fracturing simulation. Int. J. Fract. 178, 1–14 (2012)
Mikelić, A., Wheeler, M.F., Wick, T.: Phase-field modeling of a fluid-driven fracture in a poroelastic medium. Comput. Geosci. 19(6), 1171–1195 (2015)
Lee, S., Wheeler, M.F., Wick, T.: Pressure and fluid-driven fracture propagation in porous media using an adaptive finite element phase field model. Comput. Methods Appl. Mech. Eng. 305, 111–132 (2016)
Remij, E.W., Remmers, J.J.C., Huyghe, J.M., Smeulders, D.M.J.: The enhanced local pressure model for the accurate analysis of fluid pressure driven fracture in porous materials. Comput. Methods Appl. Mech. Eng. 286, 293–312 (2014)
Remmers, J.J.C., de Borst, R., Needleman, A.: The simulation of dynamic crack propagation using the cohesive segments method. J. Mech. Phys. Solids 56(1), 70–92 (2008)
Terzaghi, K.: Theoretical soil mechanics. Wiley, New York (1943)
Irzal, F., Remmers, J.J.C., Huyghe, J.M., de Borst, R.: A large deformation formulation for fluid flow in a progressively fracturing porous material. Comput. Methods Appl. Mech. Eng. 256, 29–37 (2013)
Witherspoon, P.A., Wang, J.S.Y., Iwai, K., Gale, J.E.: Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 16(6), 1016–1024 (1980)
Wells, G.N., Sluys, L.J.: A new method for modelling cohesive cracks using finite elements. Int. J. Numer. Methods Eng. 50(12), 2667–2682 (2001)
Stolarska, M., Chopp, D.L., Moës, N., Belytschko, T.: Modelling crack growth by level sets in the extended finite element method. Int. J. Numer. Methods Eng. 51(8), 943–960 (2001)
Camacho, G.T., Ortiz, M.: Computational modelling of impact damage in brittle materials. Int. J. Solids Struct. 33(20), 2899–2938 (1996)
Remmers, J.J.C., de Borst, R., Needleman, A.: A cohesive segments method for the simulation of crack growth. Comput. Mech. 31(1-2), 69–77 (2003)
Acknowledgments
This research was sponsored by the Dutch TKI Gas foundation, under grant number TKIG01025 with financial support from Baker Hughes, EBN, GDF Suez, Total and Wintershall.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Remij, E.W., Remmers, J.J.C., Huyghe, J.M. et al. On the numerical simulation of crack interaction in hydraulic fracturing. Comput Geosci 22, 423–437 (2018). https://doi.org/10.1007/s10596-017-9702-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10596-017-9702-8